A steel wire of original length 1 m and cross-sectional area 4.00 mm2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16 kg is suspended from the middle point of the wire what would be its vertical depression ?Y of the steel = 2.0 x1011 N/m2. Take g=10 m/s2.
The length of wire = L. Let the tension developed in the wire be T and the length increased = L. Strain = L/L Stress = T/A = T/4x10⁻⁶ N/m² =2.5x10⁵T N/m² The relationship between stress and strain Y*L/L = 2.5x10⁵T L = 2.5x10⁵TL/Y .................... iLet the depression of middle point = CD =d cm =0.01d m The load hung W = 2.16g =21.6 N This load is balanced by the component of tension. 2T.sinα =21.6 T = 21.6/2.sinα =10.8*CB/CD =10.8{L+L/2}/0.01d →T = 5401+L/d Putting in i L = 2.5x10⁵*5401+LL/Yd = 2.5x10⁵*5401+L/Yd →LYd = 1.35x10⁸ + 1.35x10⁸L →LYd-1.35x10⁸ =1.35x10⁸ →L2.0x10¹¹d-1.35x10⁸ = 1.35x10⁸ ------------- ii Now in the right angled triangle BCD BC² = CD² + BD² →L+L²/4 = 1x10⁻⁴d² + L²/4 →L²+2LL+L² = 4x10⁻⁴d² +L² →2LL = 4x10⁻⁴d² {neglecting L²} L = 2x10⁻⁴d² Now putting it in ii 4x10⁷d³ - 2.7x10⁴d² =1.35x10⁸ →d³ - 6.75x10⁻⁴d² - 3.375=0 {the middle term is much smaller than other two. Neglecting it we get} →d³ = 3.375 →d = 1.5 cm
Related Solutions
A steel wire of original length and cross-sectional area is clamped at the two ends so that it lies horizontally and without tension. If a load of is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel . Take
View SolutionA steel wire of original length 1 m and cross-sectional area 4.00 mm^2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16 kg is suspended from the middle point of the wire, what would be its vertical depression ?
=2.0x10^11Nm^-2. Take
View SolutionA steel wire of original length and cross-sectional area is clamped at the two ends so that it lies horizontally and without tension. If a load of is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel . Take
View SolutionAn aluminium wire and a steel wire of the same length and cross section are joined end to end. The composite wire is hung from a rigid support and the load is suspended at the free end. If Y_(AL) = 7xx10^(10) N//m^(2) and Y_("steel") = 7xx10^(11) N//m^(2) , the ratio of elongation of aluminium and steel wires is
View SolutionCalculate the work done in stretching a steel wire of length 2 m and cross sectional area 0.0225 mm2, when a load of 100 N isslowly applied to its free end. (young's Modules of steel= 2 xx 10^11 N//m^2 )
View SolutionThe area of cross section of a steel wire is . The force required to double is length will be
View SolutionThe area of cross section of a steel wire is . The force required to double is length will be
View SolutionThe area of cross section of a steel wire is . The force required to double is length will be
View SolutionThe area of cross section of a steel wire is . The force required to double is length will be
View SolutionA light rod of length of length is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section and the other is of brass of cross- section is the distance from the steel wire end, at which a weight may be hung.
Which of the following statement(s) is /are correct ?
View SolutionA light rod of length of length 2 m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10^(-3) m^(2) and the other is of brass of cross- section 2xx10^(-3) m^(2).x is the distance from the steel wire end, at which a weight may be hung. Y_(steel) = 2xx10^(11) Pa and Y_(brass) = 10^(11) Pa Which of the following statement(s) is /are correct ?
View SolutionA light rod of length of length is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section and the other is of brass of cross- section is the distance from the steel wire end, at which a weight may be hung.
Which of the following statement(s) is /are correct ?
View Solution1 m लंबे तथा अनुप्रस्थ परिच्छेद वाले स्टील के एक तार को किनारो पर क्लैंप कर दिया गया है। तार क्षैतिज दिशा में है और इस समय उसमे कोई तनाव नहीं है। यदि 2.16 kg द्रव्यमान की एक वस्तु इसके मध्यबिंदु से लटकाई जाए, तो वहाँ तार ऊर्ध्वाधर दिशा में कितना नीचे आ जाएगा? स्टील का यंग मॉड्युलस , g का मान लें।
View SolutionA mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
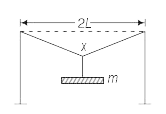
View SolutionA mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pilars show in the figure A mass m is suspended from the mid point of the wire. Strain in the wire is .
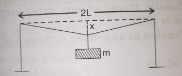
View SolutionA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
View SolutionA steel wire of length 4.7 m and cross-sectional area stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of under a given load. What is the ratio of the Young's modulus of steel to that of copper ?
View SolutionA steel wire of length 4.7 m and cross-sectional area stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionA steel wire of length 4.7 m and cross-sectional area stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionA steel wire of length 2 m and of diameter 0.8 mm is rigidly fixed at two ends horizontally ,when a load is suspended from the mid-point of the wire, a depression of 1 cm is produced. Calculate the amount of load attached, if Young's modulus for steel is .
View Solution