Twelve wires each having resistance r are joined to form a cube as shown in figure find the equivalent resistance between the ends of a face diagonal such as a and c. A 5r/7 B 3r/4 C {12r/7} D 7r/12
The correct option B 3r/4Explanation:For a cube with resistance r on its sides have equivalent resistance between ends of diagonal of one face is RAC = 3/4r
Related Solutions
Twelve wires, each having resistance r. are joined to form a cube as shown in figure. Find the equivalent resistance between the ends of a face diagonal such as a and c.
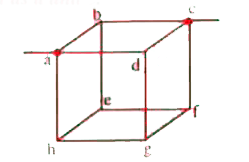
View SolutionTwelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as .

View SolutionTwelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as .

View SolutionTwelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as .

View SolutionTwelve wire, each having resistance r, are joined to form a cube.Find the equivalent resistance between the end of a face diagonal such as a and c.
View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and .

View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and .

View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and .

View SolutionTwelve identical resistance R each form a cube as shown in figure . Resistance across its face diagonal AB corners is
View SolutionTwelve identical resistance R each form a cube as shown in figure. Resistance across its face diagonal AC corners is
View Solution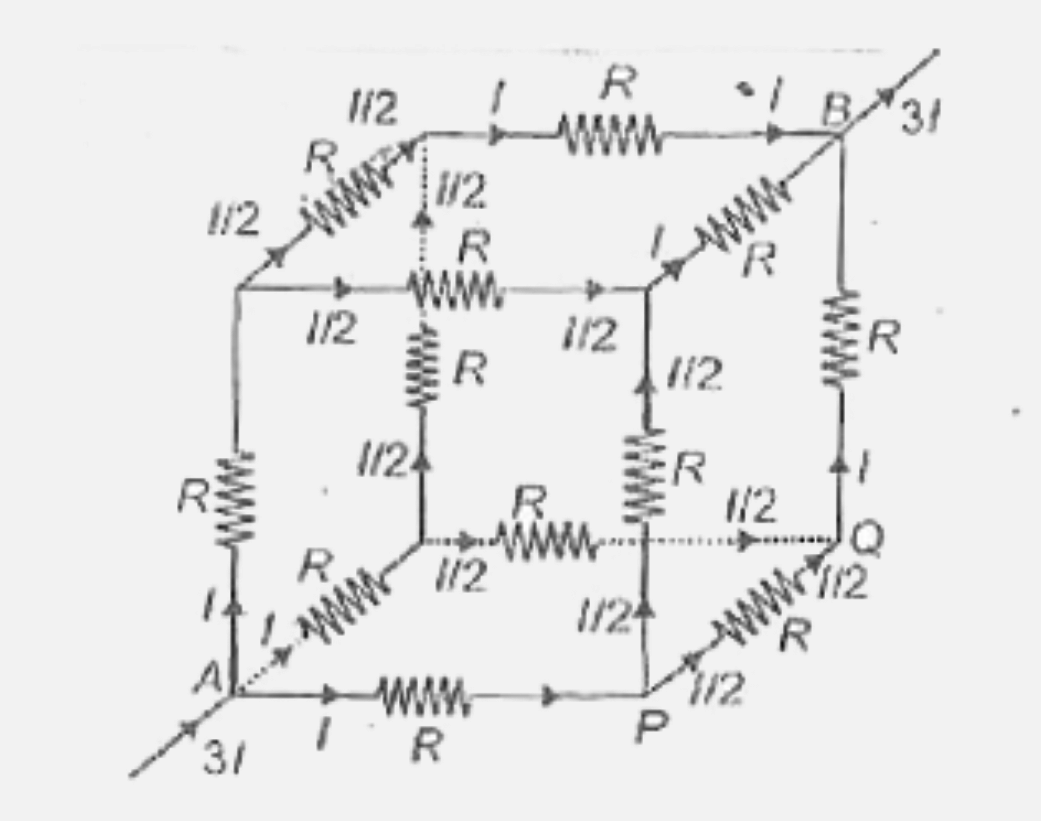
Twelve indentical resistance each of resistance R are joined to form a cube as shown in figure. Find resistance of the combination across AB.
View SolutionTwelve equal wires each of resistance r are joined to form a skeleton cube. Find the equivalent resistance between two corners on the same edge of the cube.
View SolutionTwelve identical resistors each having resistance Rare joined to form a skeleton cube. The equivalent resistance between any two diagonally opposite ends will be
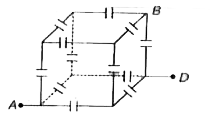
View SolutionFigure shows a combination of twelve capacitors each of capacitance C forming a cube . Find the equivalent capacitance of the combination ( a) between the diagonally opposite corners A and B of cube ( b) between the diagonally opposite corners A and D of a face of the cube .
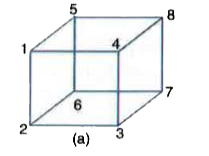
View SolutionTwelve equal wires , each of resistance r ohm are connected so as to form a skeleton cube. Find the equivalent resistance between the diagonally opposite points 1 and 7.
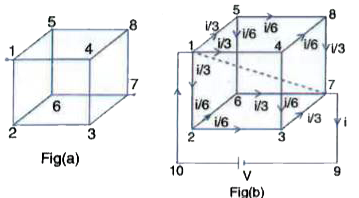
View SolutionTwelve equal wires, each of resistance r ohm are connected so as to form a skeleton cube. Find the equivalent resistance between the diagonally opposite points 1 and 7.
View SolutionThe sides of a square ABCD are formed of wires, each of resistance r and B is joined to D by a wire of resistance 2r. Find the equivalent resistance of the skelton
(i) between B and D, (ii) between A and C and (iii) between A and B.
View SolutionTwelve capacitors, each having capacitors, C , are joined to from a cube as shown. Find the equivalent capacitance between the ends of (a) Digitonal i.e., between A and B . (b) Face diagonal i.e., between A and C . (c) side of cube i.e., between A and D .
View SolutionThree identical wire rings have been placed symmetrically as shown in the figure A, B and C are centres of the three rings. Resistance of each ring is 3R. find the equivalent resistance of this wire mesh across points C and D.
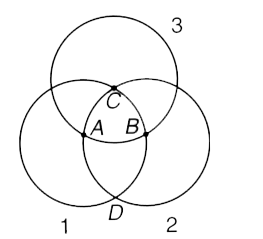
View SolutionTwelve wires, each of resistance are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View Solution