A massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended from point P such that BP is equal to x. If the fundamental frequency of the left wire is twice the fundamental frequency of right wire then the value of x isA l/5 B l/4 C 4l/5 D 3l/4
Correct option A l/5 Explanation:
Related Solutions
A massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
View SolutionA massless rod of length l of length BD is suspended by two identical massless strings AB and CD of equal length. A block of mass m is suspended from a point P such that BP is equal to x. If the original frequency of the left string is twice the original frequency of the right string, then l/x The value of:
View SolutionA massless rod is suspended by two identical strings AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to ‘x’. Further, it is observed that the frequency of 1^st harmonic (fundamental frequency) in AB is equal to 2^nd harmonic frequency in CD. Then, length of BO is
View SolutionA massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to 'x'. Further it is observed that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD . 'x' is
View SolutionA massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal ti 'x'. Further it is obsreved that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD . 'x' is
View SolutionA massless rod of length is suspened by two identical string and of equal length. A block of mass is suspended from point such that is equal to 'x'. Further it is observed that the frequency of harmonic in is equal to harmonic frequency in . 'x' is
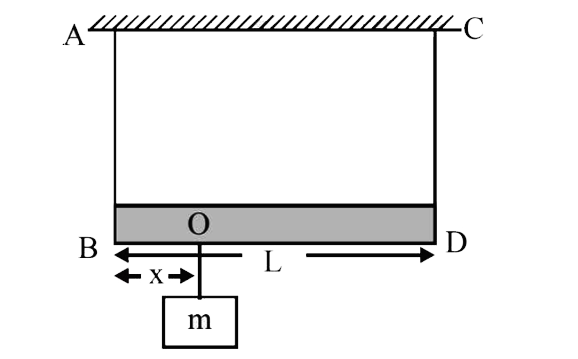
View Solutionएक द्रव्यमान छड़ BD को एक जैसी द्रव्यमानहीन डोरियों AB तथा CD द्वारा लटकायी गई है। m द्रव्यमान का एक ब्लॉक बिन्दु P से लटकाया गया है जहाँ दुरी RP , (AB = CD) x के बराबर है। यदि दायीं डोरी कि मूल आवृत्ति बायीं डोरी कि मूल आवृत्ति से दोगुनी है , तब x का मान है।
View SolutionA uniform rod AB of mass m and length l is suspended by two massless and inextensible strings AC and BD whose ends C and D are fixed as shown. Find the tension in the string BD immediately after the string at A is cut.
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png)
View SolutionIn a sonometer wire, the tension is maintained by suspending a 20kg mass from the free end of the wire. The fundamental frequency of vibration is 300Hz . If the tension is provided by two masses of 6kg and 14kg suspended from a pulley as show in the figure the fundamental frequency will
View SolutionA point mass m is suspended from the end of a massless wire of length L and cross section A. If Y is the Young's modulus for the wire, then the frequency of oscillations for simple harmonic motion along the vertical line is:
View Solutionजब द्रव्यमान M के किसी गुटके को L लम्बाई के किसी तार से निलंबित किया जाता है , तो तार की लम्बाई हो जाती है । विस्तारित तार में संचित प्रत्यास्था स्थितिज ऊर्जा है-
View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA point of mass m is suspended at the end of a massless wire of length l and cross-section A. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
[Hint: If x is the displacement of mass m from the equilibrium position then or F = (YAx)/(l) and this force acts opposite to x. Now proceed as in example 3.
View Solutionhi a sonometer wire, the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has a volume of 0.0075 m^(3) . The fundamental frequency of vibration of wire is 260 Hz. If the suspended mass is completely submerged in water, find the fundamental frequency.
View SolutionIn a sonometer wire, the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has a volume of 0.0075 m 3. The fundamental frequency of the wire is 260 Hz . If the suspended mass is completely submerged in water, the fundamental frequency will become (take ) [
View SolutionIn a sonometer wire, the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has a volume of 0.0075 m 3. The fundamental frequency of the wire is 260 Hz . If the suspended mass is completely submerged in water, the fundamental frequency will become (take g = 10 ms^(-2) ) [
View Solution