Consider a function y = 10 sin2100πt + 5 πz where y z are in cm and t is in second. A The function represents a traveling periodic wave propagating in -z direction with speed 20m/s. B The function does not represent a traveling wave. C The amplitude of the wave is 5 cm. D The amplitude of the wave is 10 cm.
Correct option C The amplitude of the wave is 5 cmExplanation: y = 51 – cos200pt + 10pz Amplitude = 5 cm
Related Solutions
Consider a function y=5.0e^((-25x^(2)-9t^(2)-30xt)) (a) Does this represent a travelling wave? (b) What is direction of propagation of the wave? (c) Find wave speed. (d) Sketch the wave at t = 0
View SolutionDoes a travelling wave in one dimension represented by a function of a linear combination of x and t,i.e., represented a travelling wave?
View SolutionDoes a travelling wave in one dimension represented by a function of a linear combination of x and t,i.e., y=f(ax+-bt) represented a travelling wave?
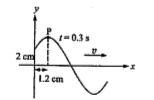
View SolutionFigures shows a snapshot of a sinusoidal travelling wave taken at t = 0.3 s. The wavelength is 7.5 cm and amplitude is 2 cm. If speed of wave is , the equation of travelling wave is:
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph. If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.
View SolutionWhich of the following wave functions does not represent a travelling wave ?
View SolutionWhich of the following wave functions does not represent a travelling wave ?
View SolutionA progressive wave is travelling along the positive direction of the x-axis. For this wave, amplitude = 5 cm, period = 0.2 s and wavelength = 30 cm
The equation of the wave using SI units is given by
View SolutionGiven below are some functions of x and t to represent the displacement of an elastic wave.
y= 5 cos (4x) sin (20t)
State which of these represent
(a) a travelling wave along (−x) direction
(b) a stationary wave (c) beats
(c) a travelling wave along (+x) direction.
Give reasons for the answers.
View SolutionIn a stationary wave represented by y=4sin(omega t) cos(kx) cm, the amplitude of the component progressive wave is
View SolutionA wave propagates on a string in positive x-direction with a speed of 40 cm/s. The shape of string at t = 2 s is y= where x and y are in centimeter. The wave equation is
View SolutionThe equation of a progressive wave is y= 1.5sin(328t-1.27x) . Where y and x are in cm and t is in second. Calcualte the amplitude, frequency, time period and wavelength of the wave.
View SolutionThe equation of a progressive wave is y= 1.5sin(328t-1.27x) . Where y and x are in cm and t is in second. Calcualte the amplitude, frequency, time period and wavelength of the wave.
View SolutionThe equation of a wave id represented as Y=2sin(Πx - 200Πt) where x and y are in cm and t is in second. The wave velocity is
View SolutionThe equation of a wave id represented as Y=2sin(Πx - 200Πf) where x and y are in cm and t is in second. The wave velocity is
View SolutionIf at , a travelling wave pulse in a string is described by the function,
Hence, are in meter and in second. What will be the wave function representing the pulse at time , if the pulse is propagating along positive x-axix with speed ?
View SolutionAt t = 0 a travelling wave pulse on a string is described by the function y=10/(x^(2) +2) , here x and y are in meter and t in second, What will be the wave function representing the pulse at time t. if the pulse is propagating along ihe positive x-axis with .speed 2m/s .?
View SolutionIf at , a travelling wave pulse in a string is described by the function,
Hence, are in meter and in second. What will be the wave function representing the pulse at time , if the pulse is propagating along positive x-axix with speed ?
View SolutionAt t = 0 a travelling wave pulse on a string is described by the function , here x and y are in meter and t in second. What will be the wave function representing the pulse at time t, if the pulse is propagating along the positive x-axis with speed 2m/s ?
View Solution