In rectangle ABCD AB = 20cm ∠BAC = 60° BC calculate side BC and diagonals AC and BD.
Consider ΔABC we getIn rectangle diagonals are equal in magnitude∴ BD = AC = 40 cm
Related Solutions
In a rectangle , calculate side and diagonals and .
View Solutionयदि आयत ABCD में , AB =20 सेमी., हो , तो भुजा BC तथा विकर्ण AC तथा BD की लम्बाई ज्ञात करो ।
View SolutionIn a rectangle , . Calculate side .
View SolutionIn a rectangle ABCD, AB= 15 cm then BC is equal to
View SolutionIn a rectangle ABCD , AB = 15 cm and , then the length of side BC is
View SolutionAB = 20 cm of a rectangle ABCD /_BAC=60^@ If BC =? And angle AC and BD =?
View SolutionABCD is a quadrilateral whose diagonals AC and BD intersect at O, prove that: (AB+BC+CD+DA)>(AC+BD)
View SolutionABCD is a quadrilateral whose diagonals AC and BD intersect at O, prove that: (AB+BC+CD+DA)>2(AC+BD)
View SolutionContruct a rectangle ABCD with diagonal AC = 6.6 cm , side BC = 5.2 cm and
View SolutionABCD is a trapezium in which and AD = BC. Show that
diagonal AC = diagonal BD
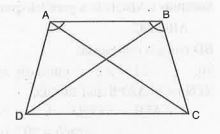
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a)
(b)

View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a)
(b)

View Solutionयदि एक चतुर्भुर्ज है जिसके विकर्ण और पर परिच्छेद करते है तो सिद्ध कीजिए की :
(ii)

View SolutionABCD एक समांतर चतुर्भुज है ।AC और BD इसके विकर्ण है । सिद्ध कीजिए -
.
View SolutionABCD is a parallelogram and AC, BD are its diagonals. Show that : vec(AC)+vec(BD)=2vec(BC),vec(AC)-vec(BD)=2vec(AB) .
View SolutionABCD is a parallelogram and AC, BD are its diagonals. Show that :
.
View Solutionare the diagonals of the parallelogram ABCD. Prove that,
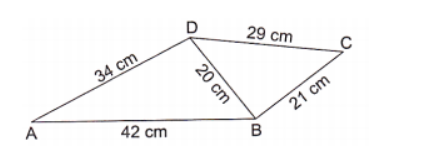
View SolutionFind the area of the quadrilateral ABCD in which in AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diagonal BD = 20 cm.
View SolutionABCD is a trapezium in which and AD = BC (See Fig.)
 Show that diagonal AC = diagonal BD.
Show that diagonal AC = diagonal BD.
View SolutionABCD is a trapezium in which and AD = BC (See Fig.)
 Show that diagonal AC = diagonal BD.
Show that diagonal AC = diagonal BD.
View Solution