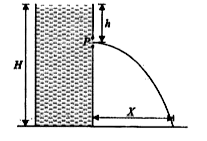
A tank is filled with water up to a height H. Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water express the horizontal distance x in terms of H and D. A x = α√[D H – D] B x = α√[{D H – D} / 2] C x = 2√[D H – D] D x = 4[D H – D]
Correct option: C x = 2√[D H – D]Explanation:We know V2 = 2ghWhere V is velocity of water coming out of the hole h is distance though which it has comeHence V = √2ghD here h = D 1Also S = 1/2 gt2 ∴ t2 = 2s / gHere s = distance travelled = H – D.Hence t2 = [{2H – D} / g] i.e. t = √[{2H – D} / g] 2∴ Horizontal distance travelled = x = V × tfrom 1 & 2 x = √[2gD] ×√[{2H – D} / g]= √[4DH – D]= 2√[DH – D]
Related Solutions
A tank is filled with water up to a height . Water is allowed to come out of a hole in one of the walls at a depth below the surface of water. Express the horizontal distance in terms of and
 .
.
View SolutionA tank is filled with water up to a height H . Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water. Express the horizontal distance x in terms of H and D .
View SolutionA tank is filled with water up to a height H. Water comes out through a hole P at a depth D above the water level. The horizontal distance in terms of x, H and D will be -
View SolutionA vessel is filled with water up to H height. Water is flowing through a hole P at a depth D from the free surface of water. By what relation will the horizontal range x be expressed in terms of H and D?
View SolutionA tank is filled with water upto a height H. Water is allowed to come out of a hole Pin one of the walls at a depth h below the surface of water (see fig.) Express the horizontal distance x in terms of H and h.
View Solutionकिसी टैंक में H ऊँचाई तक जल भरा है। जल की सतह से D गहराई पर बने छिद्र से जल निकल रहा है। जल पृथ्वी पर बर्तन से क्षैतिज दूरी x पर टकराता है। x का मान है-
View SolutionIf accelerations due to gravity at a height h and at a depth d below the surface of the earth are equal, how are h and d related ?
View SolutionLet g_(h) and g_(d) the acceleration due to gravity at height h above the earth s surface and at depth d below the earth surface respecitively if g_(n) = g_(d) then the releation between h and d is
View Solution, express d in terms of s, h and a.
View Solution, express d in terms of s, h and a.
View SolutionIf are differentiable functions of and prove that
View SolutionIf are differentiable functions of and prove that
View Solutionलकड़ी की एक गेंद , d घनत्व के पानी में h गहराई तक डुबाकर छोड़ दी जाती है , यदि लकड़ी का घनत्व D है तो गेंद पानी के बाहर इसकी सतह से किस ऊँचाई तक उछलेगी ?
View Solutionयदि D* f(x) = जहाँ
D*(tan x) का मान होगा।
View SolutionD*f(x)=lim_(h rarr0)(f^(2)(x+h)-f^(2)(x))/(h) If f(x)=x ln x then D*f(x) at x=e equals
View SolutionUsing the given diagram, express the following sets in terms of set A and B.

(i) {a,d} , (ii) {a,d,c,f}, (iii) {a,d,c,f,g,h}, (iv) {a,d,g,h}, (v) {g,h}
View SolutionThe products of the light reaction in photosynthesis are (i) ATP, water and glucose (ii) A. D. P., Water and N. A. D. P. 2 H. (iii) A. T. P., N. A. D. P. 2 H. and Oxygen.
View Solutiond घनत्व वाले जल के पृष्ठ से h गहराई पर कुल दाब है
View SolutionA right circular cylinder and a sphere are of equal volumes and their radii are also equal. If is the height of the cylinder and , the diameter of the sphere, then (b) (c) (d)
View SolutionIf a x^3+b x^2+c x+d is divisible by a x^2+c ,t h e na ,b ,c ,d are in
View Solution