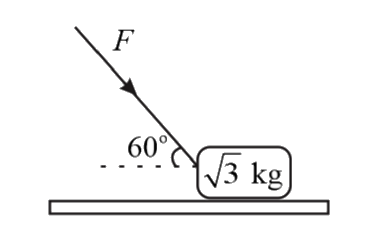
The value of force constant between the applied elastic force F and displacement will be A √3 B 1 / √3 C 1/2 D √3 /2
Correct option: B 1 / √3Explanation:F = Kxwhere F = forcex = displacementK = force constant∴ K = F/x = slope of graph F – x∴ K = tan 30 = 1 / √3
Related Solutions
The value of force constant between the applied elastic force F and displacement will be
View SolutionThe valve of force constant between the applied the applied elastic force F and displacement will be
View SolutionThe valuve of force constant between the applied elastic force F and displacement with be
View SolutionIf , then f is
View Solutionएक कण दो स्थिर बलों (4 , 1, -3) तथा (3, 1, -1) द्वारा बिन्दु (1, 2, 3) से बिन्दु (5, 4, 1) पर विस्थापित हो जाता है | सिद्ध कीजिए कि बल द्वारा किया गया कार्य 40 इकाई होगा |
View SolutionIf , then its maximum value is
(a)
(b)
(c) 1
(d)
View SolutionIf , then its maximum value is (b) (c) 1 (d)
View SolutionIf , find the value of . (b) (c) (d)
View SolutionIf , then is equal to :
( a ) 1
( b )
( c ) 2
( d )
View SolutionThe value of lies between a. b. c. d.
View Solution3 kg के पिंड पर बल लगाने से उसमे उत्पन्न विस्थापन का समीकरण मीटर है। इस बल द्वारा प्रथम 2 सेकंड में किया गया कार्य होगा-
View SolutionA force vec(F) = 3 hat(i) + 2hat(j) - 4hat(k) is applied at the point (1, -1, 2) . What is the moment of the force about the point (2 , -1, 3) ?
View SolutionThe metal blocks A and B of masses 2 kg and 1 kg , respectively are in contact on a frictionless table A constant horizontal force of 3 N is applied to the block A . Calculate the force of constant between the two blocks . If the same force is applied to the block B then what will be the force of contact ? Can you explain the difference ?
View SolutionA force F is applied on a block of mass which rests on a horizontal surface with a coefficient of friction . The maximum value of F for which the block doesn't move, is [Take
View SolutionThe value of is a. b. c. d.
View SolutionOn applying a force F the mass M is displaced vertically down by y from equilibrium position. Find the force F in terms of the force constant k of the spring d displacement y, for the cases (A) and (B), as, shown in figure
View SolutionThe mass force of one m mass vec F = (3hati +2hatj + 4hatk)N Under the influence of, point A (3, 1, 2) is displaced from point B (4, 3, 3). Calculate the work done by the force.
View Solution|(1,a,a^2,a^3+bcd),(1,b,b^2,b^3+cda),(1,c,c^2,c^3+abd),(1,d,d^2,d^3+abc)| =
View SolutionTabular |(1,a,a^(2),a^(3),+bcd),(1,b,b^(2),b^(3),+cda),(1,c,c^(2),c^(3),+dab),(1,d,d^(2),d^(3),+abc)| Assume
View SolutionProve that |[1,a,a^2,a^3+bcd] , [1,b,b^2,b^3+cda] , [1,c,c^2,c^3+dab] , [1,d,d^2,d^3+abc]|=0
View Solution