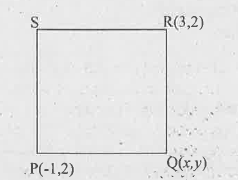
The two opposite vertices of a square are –1 2 and 3 2. Find the coordinates of the other two vertices.
Solution: Let ABCD be a square and A –1 2 and C 3 2 be the given vertices. Let the coordinates of vertex B be x y.AB = BC As ABCD is a squareAB2 = BC2[x – –1] 2 + y – 22 = x – 32 + y – 22 x + 12 = x – 32x 2 + 2x + 1 = x 2 – 6x + 92x + 6x = 9 – 18x = 8x = 1In ΔABC we have:AB2 + BC2 = AC2 Pythagoras theorem2AB2 = AC2 Since AB = BC2[x – –12 + y – 22] = 3 – –12 + 2 – 222[x + 12 + y – 22] = 42 + 022[1 + 12 + y – 22] = 16 x = 12[ 4 + y – 22] = 168 + 2 y – 22 = 162 y – 22 = 16 – 8 = 8y – 22 = 4y – 2 = ± 2y – 2 = 2 or y – 2 = –2y = 4 or y = 0Thus the other two vertices of the square ABCD are 1 4 and 1 0.
Related Solutions
ಒಂದು ಚೌಕದ ಎರಡು ಅಭಿಮುಖ ಶೃಂಗಗಳ ನಿರ್ದೇಶಾಂಕಗಳು ಮತ್ತು ಆಗಿವೆ. ಉಳಿದೆರಡು ಶೃಂಗಗಳನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View SolutionTwo opposite vertices of a square are and . Find the coordinates of other two vertices.
View SolutionThe two opposite vertices of a square are and Find the coordinates of the other two vertices.
View SolutionThe two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two vertices.
View SolutionThe two opposite vertices of a square are (-1,2) and (3, 2). Find the coordinates of the other two vertices.
View SolutionThe two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two vertices.
View SolutionThe coordinates of two point opposite vertices oc a square are (3,4) and (1,-1), find the coordinates of the other two vertices.
View Solutionकिसी वर्ग के दो सम्मुख शीर्ष (-1, 2) और (3, 2) हैं | वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए |
View Solutionएक वर्ग के दो सम्मुख शीर्ष क्रमश (0, 3) और (4, 3) है । वर्ग के अन्य शीर्षों के निर्देशांक ज्ञात कीजिए ।
View SolutionTwo opposite vertices of a square are (1,-2) and (-5,6), then the other two vertices are
View SolutionQ.7 The two opposite vertices of a square are (l.-6)and (5,4). Find the coordinates of the other two vertices.
View SolutionQ.7 The two opposite vertices of a square are (l.-6)and (5,4). Find the coordinates of the other two vertices.
View SolutionThe two opposite vertices of a square are (1,-6)and (5,4). Find the coordinates of the other two vertices.
View SolutionIf A(3, 4) and C (1, -1) are two opposite angular points of square ABCD, find the coordinates of other two vertices.
View SolutionTwo opposite vertices of a square are . Find the coordinates of the other vertices.
View Solutionএকটি বর্গক্ষেত্রের দুটি বিপরীত শীর্ষবিন্দুর স্থানাঙ্ক (0,-1) এবং (0,3) হলে তার অপর শীর্ষবিন্দু দুটির স্থানাঙ্ক হবে-
View SolutionIf the two adjacent vertices of a square are (3,4)and (1,-1,) then find the length of the diagonal.
View SolutionIf two opposite vertices of a square are (1,2) and (5,8) find the coordinates of its other two vertices and the equations of its sides.
View SolutionIf two opposite vertices of square are (1,2) and (5,8), find the coordinates of its other two vertices and the equations of its sides.
View SolutionTwo opposite vertices of a square are and . Find the coordinates of other two vertices.
View Solution