Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are 0 –1 2 1 and 0 3. Find the ratio of this area to the area of the given triangle.
Solution:Let the vertices of the triangle be A 0 -1 B 2 1 C 0 3.Let D E F be the mid-points of the sides of this triangle. Coordinates of D E and F are given byD = 0+2/2 -1+1/2 = 1 0E = 0+0/2 -3-1/2 = 0 1F = 2+0/2 1+3/2 = 1 2Area of a triangle = 1/2 {x1 y2 - y3 + x2 y3 - y1 + x3 y1 - y2}Area of ΔDEF = 1/2 {12-1 + 11-0 + 00-2} = 1/2 1+1 = 1 square unitsArea of ΔABC = 1/2 [01-3 + 2{3--1} + 0-1-1] = 1/2 {8} = 4 square unitsTherefore the required ratio is 1:4.
Related Solutions
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of the area of the triangle formed to the area of the given triangle
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are ( 0 , - 1) , ( 2 , 1) and ( 0 , 3) . Find the ratio of this area to the area of the given triangle .
View SolutionFind the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are (0,-1), (2,1) and (0,3) . Find the ratio of this area to the area of the given triangle .
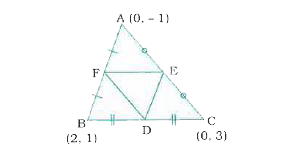
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid–points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of the area of the triangle formed to the area of the given triangle
View SolutionFind the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are (0,-1), (2,1) and (0,3) . Find the ratio of this area to the area of the given triangle .

View Solutionबिन्दुओ तथा (0 ,3 ) शीर्ष वाले त्रिभुज की भुजाओं के मध्य बिंदुओं को मिलाने पर बने त्रिभुज का क्षेत्रफल ज्ञात कीजिये तथा इस प्रकार बने त्रिभुज के क्षेत्रफल व दिए गए त्रिभुज के क्षेत्रफल का अनुपात भी ज्ञात कीजिये|
View Solutionशीर्षो (0,-1),(2,1) और (0,3) वाले त्रिभुज की भुजाओं के मध्य-बिंदुओं से बनाने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए। इस क्षेत्रफल का दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए।
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,-1),(2,1) and (0,3).Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle, whose vertices are (2, - 4), (6, 2) and (- 4, 6). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid -points of the sides of the triangle ABC ,whose vertices are A(0,-1),B(2,1)andC(0,3).
View SolutionFind the area of the triangle formed by joining the mid–points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View Solutionਸਿਖਰਾਂ (0,-1),(2,1) ਅਤੇ (0,3) ਵਾਲੇ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂਆਂ ਤੋਂ ਬਨਣ ਵਾਲੇ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ। ਇਸ ਖੇਤਰਫਲ ਦਾ ਦਿੱਤੇ ਹੋਏ ਤ੍ਰਿਭੁਜ ਦੇ ਖੇਤਰਫਲ ਨਾਲ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ।
View Solutionशीर्षो (0, -1), (2, 1) और (0, 3) वाले त्रिभुज की भुजाओ के मध्य-बिन्दुओ से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए । इस क्षेत्रफल का दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए ।
View SolutionFind the area of the triangle formed by the mid points of sides of the triangle whose vertices are (2,1),1-2,3),(4,-3)
View Solution