If 2tanα + cotβ = tanβ then tanβ – α = __________ a tanαb cotα c tanβ d cotβ
The correct option d cotβ Explanation:given: 2tanα + cotβ = tanβ∴ 2tanα = tanβ – cotβ∴ tanα = [tanβ – cotβ/2]∴ tanβ – α = [tanβ – tanα/{1 + tanβ ∙ tanα}]= [{tanβ – [tanβ/2] + [cotβ/2]}/{1 + [tan2β/2] – 1/2}]= [{[tanβ/2] + [cotβ/2]}/{1 + tan2β/2}]= [tanβ + cotβ/1 + tan2β]= [{tanβ + [1/tanβ]}/1 + tan2β]= [1 + tan2β/{tanβ1 + tan2β}]= cotβ.
Related Solutions
lf α and β are two different solutions lying between −π/2 and π/2 of the equation 2tanθ+Secθ=2 then tanα+tanβ
View SolutionIf the tangents to the ellipse a 2 x 2 + b 2 y 2 =1 make angles α and β with the major axis such that tanα+tanβ=λ, then the locus of their point of intersection is
View SolutionIf then − =? (A) (B) (C) (D)
View SolutionDraw the structure of α-D glucopyranose.
View SolutionIf are the roots of the equation ,where then (a) 0<α<β (b) (c) α<β<0 (d)
View SolutionIf is such that then
View SolutionIf the equation ax^2+bx+c=0(a>0) has two roots α and β such that α 2 , then: a) b^2-4ac>0 b) c 0 d) 4a+2|b|+c <0
View Solution13 . a r e ∈ H . P . t h e n : A ) B ) C ) D )
View Solutionयदि द्विघात बहुपद ax^2+bx+c के शून्यक α और β हो, तो α+β का मान होगा:
View SolutionThe number of ordered pairs (α,β), where α,β∈(−π,π) satisfying cos (α−β)=1 and cos(α+β)=1/e is
View SolutionThe number of ordered pairs (α,β), where α,β∈(−π,π) satisfying cos (α−β)=1 and cos(α+β)=1/e is
View SolutionIf cos(α−β)=1 and cos(α+β)= 1/e , where α, β∈[−π,π]. Then number of ordered pairs of (α,β) is
View SolutionHow many As are there in the following series which are immediately followed by B as well as immediately preceded by Z?
A Μ Β Ζ Α Ν Α Α Β Z A B
A Z Β Α Ρ Z Α Β Α Ζ Α Β
View SolutionInand bisector of meets AB in D (Fig. 6.17). Measure of is.
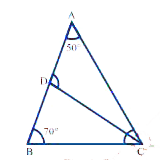
View SolutionBenzoin is Compound containing an aldehyde and a ketonic group α , β -unsaturated acid α -hydroxyaldehyde α -hydroxyketone
View SolutionIf sin(120° – α) = sin(120° – β) and 0 < α, β < π then find the relation between α and β.
View SolutionIf sin(120° – α) = sin(120° – β) and 0 < α, β < π then find the relation between α and β.
View SolutionDefine carbohydrates. Draw the Haworth projection structures of the following.
α-D-(-) fructofuranose
View SolutionDegree OF Dissociation (α) || Mavg and Vapour Density in Terms OF α
View Solutioncosαsin(β−γ)+cosβsin(γ−α)+cosγsin(α−β)=
View Solution