If the equation of the locus of a point equidistant from the points a1 b1 and a2 b2 is a1 – a2x + b1 b2y + c = 0 then the value of C will bea 1/2a22 + b22 – a12 – b12b a12 – a22 + b12 – b22c1/2a12 + a22 + b12 + b22d √a12 + b12 – a22 – b22
The correct option a 1/2a22 + b22 – a12 – b12Explanation:Let Px y be point equidistant from Aa1 b1 and Ba2 b2 from Aa1 b1 and Ba2 b2∴ PA2 = PB2∴ x – a12 + y – b12 = x – a22 + y – b22∴ 2xa1 – a2 + 2yb1 – b2 + a22 + b22 – a12 – b12 = 0∴ a1 – a2x + b1 – b2y + 1/2a22 + b22 – a12 – b12 = 0given equation of locus: a1 – a2x + b1 – b2y + c = 0∴ comparing we get C = [a22 + b22 – a12 – b12/2]
Related Solutions
If the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2)
View SolutionIf the equation of the locus of a point equidistant from the points and is , then the value of is
View SolutionVitamin B1 , B2 , B3 , B6 , B12 and Vitamin C are .................. soluble vitamins .
View SolutionLe be real numbers satisfying for If then the value of is equals to _______.
View SolutionA(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X-அச்சு எந்த விகிதத்தில் பிரிக்கும்?
View SolutionIn a , If , then is
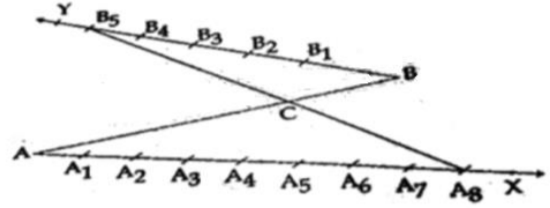
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
View Solutionসংখ্যারেখা তৈরি করে নীচের সংখ্যাগুলিকে সংখ্যারেখায় দেখাও ও নাম দাও। +5, -2, +3, -6, +2, -5, -এ যথাক্রমে A,B,C,D,E ও F নাম দাও। B থেকে E-এর দূরত্ব কত ঘর মেপে দেখো।
View SolutionSuppose A1,A2,…..A30 are thirty sets each having 5 elements and B1,B2,…….Bn are n sets each having 3 elements.Let each elements of S belongs to exactly 10 of A1,'s and exactly 9 of B1's.Then find the value of n.
View Solutionविटामिन B12 में कौन - सी धातु उपस्थित होती है ?
View Solutionwhich metal is present in vitamin or cyanocobalamin?
View SolutionWrite chemical name of Vitamin .
View SolutionThe ratios a1/a2 , b1/b2 , c1/c2 Find out whether the given linear equations are pairwise compatible or incompatible: 2x - 3y = 8 and 4x - 6y = 9.
View SolutionName the factor essential for absorption of vitamic B12
View SolutionName the factor essential for absorption of vitamin B12
View SolutionIntrinsic factor that helps in the absorption of vitamin B12 is secreted by :-
View SolutionWhich of the followings is NOT a rich source of Vitamin B12?
View SolutionIntrinsic factor that helps in the absorption of vitamin B12 is secreted by :-
View SolutionWhich metal ion is present in Vitamin B12?
View SolutionVitamin B12 is produced directly during course of fermentation by
View Solution