A circular disc of mass m and radius r is rolling on a smooth horizontal surface with a constant speed v. Its kinetic energy is _____ A 1/4 mv2 B 1/2 mv2 C 3/4 mv2 D mv2
Correct option: C 3/4 mv2Explanation:KE = 1/2mv2 + 1/2Iω2 --- both rotational and translation kinetic energies for disc I = [mR2 / 2]KE = 1/2mv2 + 1/2 ×[mR2 / 2] × v/R2 ----- v = rω= 1/2mv2 + 1/4mv2 = 3/4mv2
Related Solutions
A loop of mass M and Radius R is rolling on a smooth horizontal surface with speed 'V'. Its total kinetic energy
View SolutionA loop of mass M,and radius R is rolling on a smooth horizontal surface with speed 'v'. Its total kinetic energy is
View SolutionA loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
View SolutionIf a disc of mass 400 gm is rolling on a horizontal surface with uniform speed of 2 m/s, then its rolling kinetic energy will be
View SolutionIf a disc of mass 400 gm is rolling on a horizontal surface with uniform speed of 2 m/s, then its rolling kinetic energy will be
View SolutionA disc of mass 4 kg and of radius 1 m rolls on a horizontal surface without slipping such that the velocity of its centre of mass is 10 cm sec^(-1) . Its rotational kinetic energy is
View SolutionA disc of mass 4 kg and of radius 1 m rolls on a horizontal surface without slipping such that the velocity of its centre of mass is 10" cm sec"^(-1) , Its rotatonal kinetic energy is
View Solution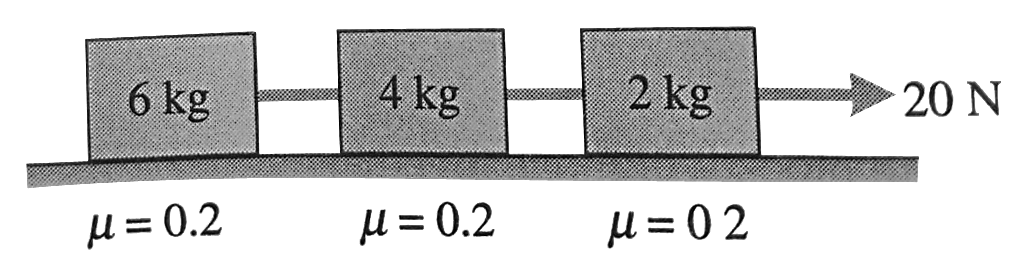
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA circular disc of mass M and radius r is set rolling on a table. If omega be its angular velocity, show that its total K.E. is given by (3//4)M v^(2), where v is its linear velocity M.I. of circular disc = (1//2) mass xx (radius)^(2) .
View SolutionA circular disc of mass m and radius r is rolling over a horizontal table top with angular velocity omega . Prove that the total energy of the disc , K = (3)/(4) m omega ^(2) r^(2) .
View Solutionएक M द्रव्यमान एवं R त्रिज्या का ठोस गोला क्षैतिज सतह पर बिना फिसले लुढ़कता है। घूर्णन गतिज ऊर्जा एवं कुल ऊर्जा का अनुपता होगा :-
View SolutionDisc is rolling on the horizontal with constant If mass of the disc is velocity 2 m/s. 400 g, then total kinetic energy of disc is
View SolutionA body rolls over a horizontal, smooth surface without slipping with a translational kinetic energy . Show that the total kinetic energy of the body is where is the radius of gyration and is the radius of the body. Using the above relation. Find the total kinetic energy of a circular disc.
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View Solutionजमीन पर लुढ़कती ठोस गेंद (द्रव्यमान m, त्रिज्या r) की कल गतिज ऊर्जा ज्ञात कीजिए यदि उसका राखक वेग v है।
View SolutionA dices of mass M and radius R rolls without slipping on a leveled surface with a linear speed v. what is its kinetic energy?
View SolutionA uniform disc of mass m , radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F = 4 N, m= .1 kg, R = 1 m and r = 1/2 m then, find the: angular acceleration of the disc. (rads^(-1))
View SolutionA uniform disc of mass m , radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F = 4 N, m= .1 kg, R = 1 m and r = 1/2 m then, find the: angular acceleration of the disc. (rads^(-1))
View SolutionA solid cylinder of mass 1 kg and radius 0.02 m, is rolling on a smooth horizontal surface with a uniform velocity of 0.1 m/s. Its total energy is
View Solution