If perpendicular distance from 0 0 0 to the variable plane is p and variable plane intersects the axis in A B C the centroid of ΔABC is on 1/x2 + 1/y2 + 1/z2 = ____A 9/p2B p2/9C p/9D 9/p
The correct option A 9/p2 Explanation:point on axis Aa 0 0 B0 b 0 and C0 0 ccentroid of ΔABCx1 y1 z1 = [a/3 b/3 c/3] A B C satisfied plane x/a + y/b + z/c = 1also distance from 0 0 0 to plane is p∴ p = [1/√{1/a2 + 1/b2 + 1/c2}]∴ 1/p2 = 1/a2 + 1/b2 + 1/c2∴ 1/p2 = [1/9x12] + [1/9y12] + [1/9z12]centroid of ΔABC is on 1/x2 + 1/y2 + 1/z2 = 9/p2.
Related Solutions
Let be the equation of a plane passing through the line of intersection of the planes and perpendicular to the plane Then the points which lie on the plane is/are a. b. c. d.
View SolutionA variable plane which remains at a constant distance P from the origin (0) cuts the coordinate axes in A, B and C
View SolutionA variable line passing through the point P(0, 0, 2) always makes angle 60^(@) with z-axis, intersects the plane x+y+z=1 . Find the locus of point of intersection of the line and the plane.
View SolutionA variable line passing through the point P(0, 0, 2) always makes angle 60^(@) with z-axis, intersects the plane x+y+z=1 . Find the locus of point of intersection of the line and the plane.
View SolutionIf be two non-parallel planes, then the equation represents the family of all planes through the line of intersection of the planes except the plane :
View SolutionIf be two non-parallel planes, then the equation represents the family of all planes through the line of intersection of the planes except the plane :
View SolutionA variable plane intersects the co- ordinate axes at a distance from .Then the locus of the centroid of the tetrahedron OABC is.....
View SolutionA variable plane is at a constant distance p from the origin and meets the axes in A, B and C. The locus of the centroid of the tetrahedron OABC is
View SolutionA variable plane is at a constant distance p from the origin and meets the axes in A, B and C. The locus of the centroid of the triangle ABC is
View SolutionA variable plane is at a constant distance p from the origin and meets the axes in A, B and C. The locus of the centroid of the triangle ABC is
View SolutionA variable plane is at a constant distance P from the origin and meets the axes in A, B and C. The locus of the centroid of tetrahedran OABC is
View Solution(i) A variable plane, which remains at a constant distance '3p' from the origin cuts the co-ordinate axes at A, B, C. Show that the locus of the centroid of the triangle ABC is :
.
(ii) A variable is at a constant distance 'p' from the origin and meets the axes in A, B, C respectively, then show that locus of the centroid of th triangle ABC is :
View SolutionConsider the plane and the point P(1,-2,3).
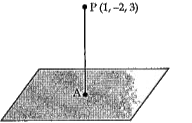
Distance between and P is _______ units.
View SolutionIf the distance of the point from the plane then the foot of the perpendicular from to the place is a. b. c. d.
View SolutionIf the distance of the point P(1,-2,1) from the plane , where , is 5, then the foot of the perpendicular from P to the plane is:
View SolutionA point P moves on a plane (x)/(a)+(y)/(b)+(z)/(c)=1 . A plane through P and perpendicular to OP meets the coordinate axes in A, B and C. If the planes throught A, B and C parallel to the planes x=0, y=0 and z=0 intersect in Q, then find the locus of Q.
View SolutionA point P moves on a plane . A plane through P and perpendicular to OP meets the coordinate axes in A, B and C. If the planes throught A, B and C parallel to the planes intersect in Q, then find the locus of Q.
View SolutionLet there are three points and in x – y plane. The distance from a variable point P to the line BC is the geometic mean of the distances from this point to lines AB and AC then locus of P can be
View SolutionLet there are three points and in x – y plane. The distance from a variable point P to the line BC is the geometic mean of the distances from this point to lines AB and AC then locus of P can be
View SolutionA variable plane is at a constant distance p from the origin and meets the axes at A,B,C. Through A,B,C plane are drawn parallel to the co-ordinate planes. Show that the locus of their points of intersection is .
View Solution