Line L: vector r = 8 – 9 10 + k3 – 16 7 k ∈ R and M: vector r = 15 29 5 + k3 8 – 5 k ∈ R. If P ∈ L Q ∈ M where PQ is shortest distance between L and M then PQ = ____A √14B 14C 1/14D 1/√14
The correct option B 14Explanation:Line L: vector r = 8 – 9 10 + k3 – 16 7 = 8 + 3k – 9 – 16k 10 + 7kLet P ∈ L P = 8 + 3k1 – 9 – 16k1 10 + 7k1 ....1 Line M: vector r = 15 + 3k 29 + 8k 5 – 5kLet Q ∈ M then Q = 15 + 3k2 29 + 8k2 5 – 5k2 .....2∴ vector PQ = 7 + 3k2 – 3k1 38 + 8k2 + 16k1 – 5 – 5k2 – 7k1also vector ℓ = 3 – 16 7 and m = 3 8 – 5vector PQ is shortest distance between L and M.hence vector PQ ⊥ vector L and vector PQ⊥ vector M∴ vector PQ ∙ vector ℓ = 0 ∴ 37 + 3k2 – 3k1 – 1638 + 8k2 + 16k1 + 7– 5 – 5k2 – 7k1 = 0∴ 77k2 + 157k1 + 311 = 0 .......3similarly vector PQ ∙ vector m = 0 ∴ 37 + 3k2 – 3k1 + 838 + 8k2 + 16k1 – 5– 5 – 5k2 – 7k1 = 0∴ 98k2 + 154k1 + 350 = 0 ∴ 49k2 + 77k1 + 175 = 0 .... 4 ∴ k1 = – 1 and k2 = – 2 ∴ from eqn 1 P = 5 7 3 and Q = 9 13 15 ∴ vector PQ = 4 6 12 ∴ vector |PQ| = √16 + 36 + 144 = 14 unit.
Related Solutions
The position vector of P and Q are respectively a and b. If R is a point on PQ such that PR = 5 PQ, then the position vector of R is
View SolutionThe position vectors of P and Q are respectively a and b. If R is a point on such that , then the position vector of R is
View SolutionIf P - Q - R , l(PR) = 7 units , l(PQ) = 4 units , l(QR) =
View SolutionIn if and and are the mid-points of the sides and respectively. Prove that
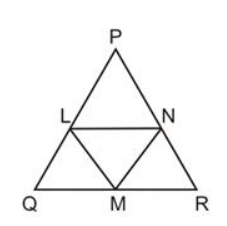
View SolutionIn if and and are the mid-points of the sides and respectively. Prove that
View Solutionमाना L समतल में सभी रेखाओं का समुच्चय है तथा L पर परिभाषित सम्बन्ध R इस प्रकार है कि R={(l,m),l,m पर लम्बवत है }.
View SolutionIf M=|(a,l,p),(b,m,q),(c,n,r)|,N=|(p,q,r),(a,b,c),(l,m,n)| Then
View SolutionIf M=|(a,l,p),(b,m,q),(c,n,r)|,N=|(p,q,r),(a,b,c),(l,m,n)| Then
View SolutionLet det and if , then the value equals :
View SolutionLet det and if , then the value equals :
View SolutionLet det and if , then the value equals :
View SolutionLet and . If , then the value of is_______
View SolutionIf k=1,l=2,m=0,p=3,q=4,r=5 then find the values of (3k^2)/p^2 and (kr^k)/q^l
View Solutionसिद्ध कीजिए कि बिंदु P(-3,-2,4) , Q(-9-8-10) व R(-5,-4,6) संरेख हैं तथा R,PQ को 1:2 के अनुपात में बाँटता हैं ।
View SolutionIf p, lines l and m are perpendicular to each other q: the point on the line m is R and r: R is a point on the line m that is perpendicular to l. The fertilization of the thirty-one is
View SolutionIf p, lines l and m are perpendicular to each other q: the point on the line m is R and r: R is a point on the line m that is perpendicular to l. The preamble of this statement is the same statement
View SolutionA man's speed with the current is 15 km / hr and the speed of the current is 2.5 km/ hr. The man's speed against the current is: b. c. d.
View SolutionDimensions of are
View SolutionThe position vectors of P and Q are respectively . If R is a point on such that then the position vector of R, is
View SolutionThe position vectors of P and Q are respectively . If R is a point on such that then the position vector of R, is
View Solution