Constant term in expansion of 1 + x/2 - 2/x4 is .......a 5 b -5 c 4 d -4
Correct option: b -5Explanation:[1 + x/2 – 2/x]4 = [1 + {x/2 – 2/x}]4 = 4c0 + 4c1 [x/2 – 2/x] + 4c2 [x/2 – 2/x]2 + 4c3 [x/2 – 2/x]32/x]3 + 4c4 [x/2 – 2/x]4 = 1 + 4[x2 – 4 / 2x] + 6[x4 – 8x2 + 16 / 4x2] + [4 / 8x3] x6 – 12x4 + 48x2 – 64 + x4 / 16 – x2 + 6 – 16 / x2 + 16 / x4= 1 + 2x – 8/x + 3/2x2 – 12 + 24 / x2 + x3 / 2 – 6x + 24 / x – 32 / x3 + x4 / 16 – x2 + 6 – 16 / x2 + 16 / x4= – 5 – 4x + 16 / x + x2 / 2 + x3 / 2 + x4 / 16 + 8 / x2 – 32/ x3 + 16 / x4hence constant term is – 5.
Related Solutions
The coefficient of x^5 in the expansion of (1+x^2)(1+x)^4 is (a) 12 (b) 5 (c) 4 (d) 56
View SolutionIf in the expansion of the sum of 5th and 6th terms is 0, then the values of a. b. c. d.
View SolutionIf in the expansion of the sum of 5th and 6th terms is 0, then the values of b. c. d.
View SolutionThe power of x in the term with the greatest coefficient in the expansion of is a)2 b)3 c)4 d)5
View SolutionFind the number of terms in the expansion of .
View SolutionThe number of terms which contain variables in the expansion of (x+(1)/(x)+1)^(2) (A) 6 (B) 5 (C) 4 (D) 3
View Solutionmatch the columns
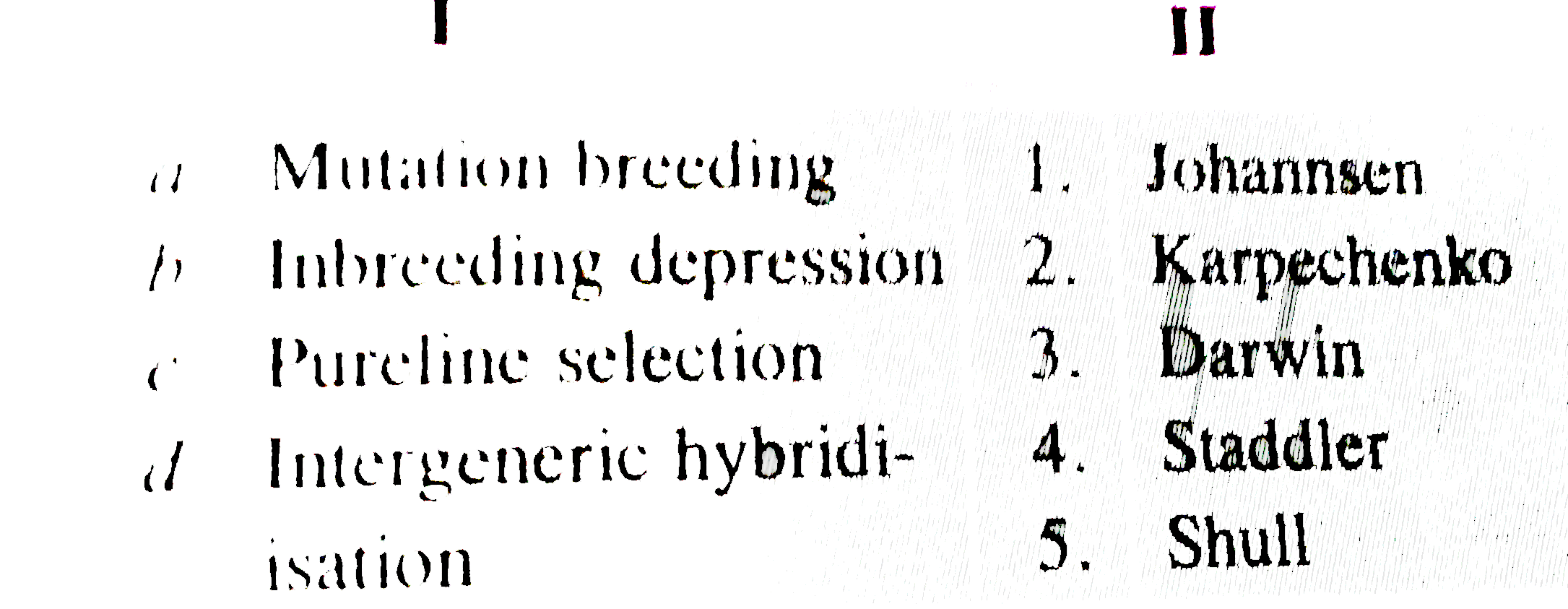
(a) a -4, b-2,c-5,d-1
(b) a-4,b-5,c-2,d-1
(c) a-4,b-5,c-1,d-2
(d) a-5, b-4,c-1,d-2
View SolutionThe first 3 terms in the expansion of (a-5x)^(-2) are (1)/(4)+(5)/(4)x+bx^(2). Find the value of a, the value of b and the term in x^(3)?
View SolutionThe coefficient of x^5 in the expansion of (1+x^2)^5+(1+x)^4 is (A) 30 (B) 60(C) 40(D) none of these
View SolutionThe constant term in the expansion of is equal to a) b) c) d)
View Solutionis equal to
View Solutionis equal to
View SolutionThe term independent of x in the expansion of is (A) (B) (C) (D)
View SolutionIf the third term in expansion of is then is equal to (a) (b) (c) (d)
View SolutionIf the third term in expansion of is then is equal to (a) (b) (c) (d)
View SolutionIf the third term in expansion of is then is equal to (a) (b) (c) (d)
View SolutionThe coefficient of in the expansion of is
View SolutionThe coefficient of x^(5) in the expansion of (1+(x)/(1!)+(x^(2))/(2!)+(x^(3))/(3!)+(x^(4))/(4!)+(x^(5))/(5!))^(2) is
View SolutionFind x such that the four points , , and are coplanar
View SolutionFind x such that the four points A(3, 2, 1), B(4, x, 5), C(4, 2, -2) and D(6, 5, -1) are coplanar.
View Solution