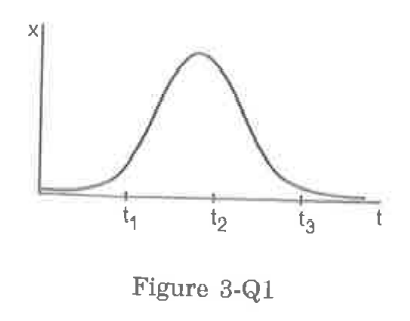
Figure 3-Q1 shows the x- coordinate of a particle as a function of time. Find the signs of vx and ax at t=t1 t= t2 and t=t3.
If x and x be the x-coordinate of the particle at initial time t and t respectively then vx =x-x/t-t = tanθ. For t-t infinitesimally small it is the vx at that instant. So slope of the tangent at any point in the above graph gives vx . At t=t1 tanθ is positive so sign of vx is positive. At t= t2 the slope of the curve is horizontal so tanθ=0 → vx =0. At t=t3 the slope of the curve is negative so sign of vx is negative.
Related Solutions
Figure shows the x coordinate of a particle as a function of time. Find the signs of at ,.
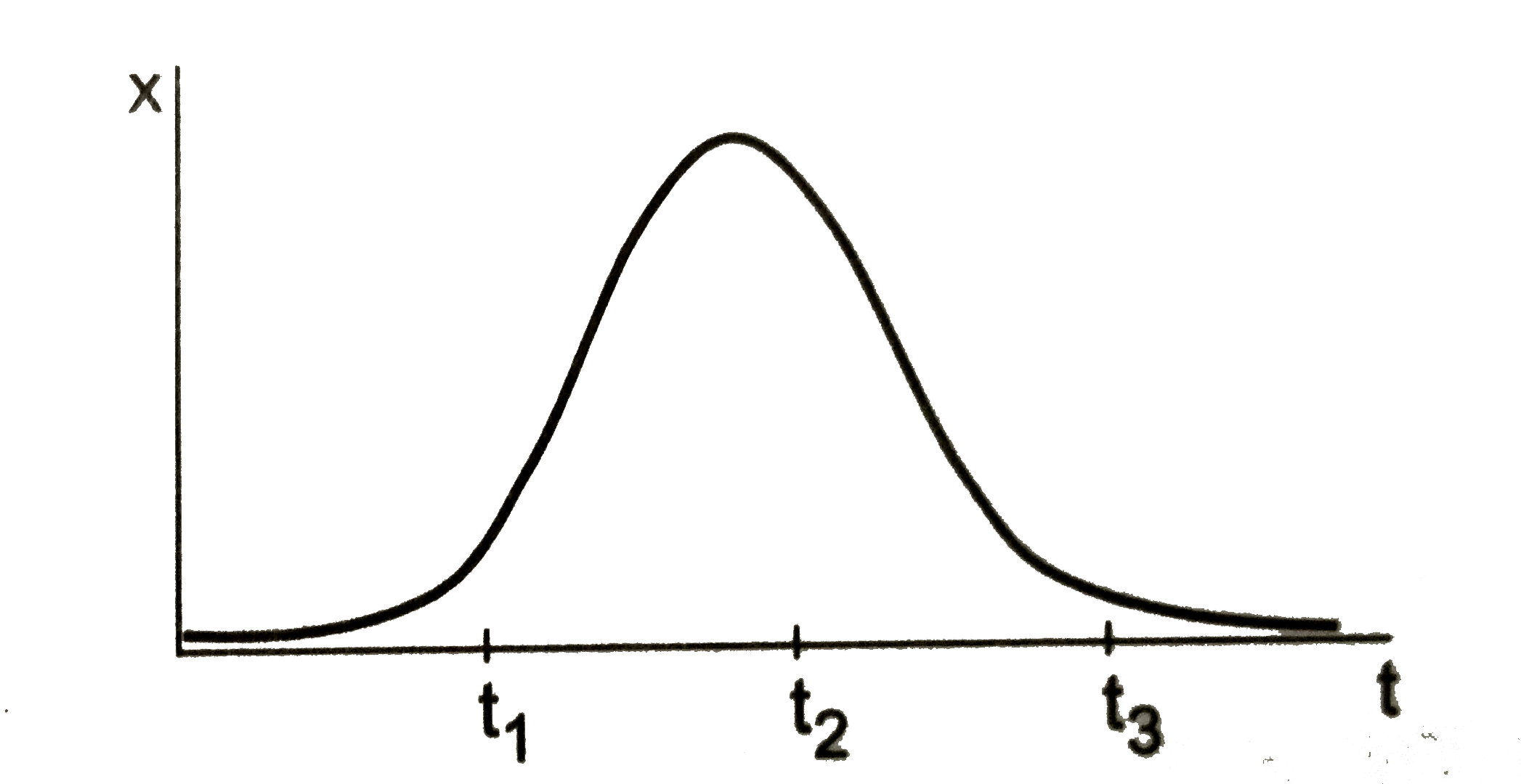
View SolutionFigure shows the x coordinate of a particle as a function of time. Find the signs of , t=t_2 and t=t_3.

View SolutionWrite the corect number in the given boxes from the following
. Here,
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t = t_1 and t = t_2.
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time

View SolutionThe displacement x of a particle with a function of time t is shown in the figure. The graph shows that
View SolutionThe coordinates of a moving particle at any time t are given by x = alpha t^(3) and y = beta t^(3) . The speed of the particle at time t is given by
View SolutionThe coordinates of a moving particle at any time 't' are given by x= alpha t^(3) and y= beta t^(3) . The speed of the particle at time 't' is given by
View SolutionThe coordinates of a moving particle at any time are given by and . The speed of the particle at time is given by
View Solutiont1, t2, t3, ... என்பது ஒரு கூட்டுத் தொடர் வரிசை எனில், t6, t12, t18 , .... என்பது.
View Solutiont 1 and t 2 are two points on the parabola . If the focal chord joining them coincides with the normal chord, then t1+t2=0 (d) none of these
View Solutiont 1 and t 2 are two points on the parabola . If the focal chord joining them coincides with the normal chord, then t1+t2=0 (d) none of these
View Solutiont 1 and t 2 are two points on the parabola . If the focal chord joining them coincides with the normal chord, then t1+t2=0 (d) none of these
View Solutiont 1 and t 2 are two points on the parabola . If the focal chord joining them coincides with the normal chord, then t1+t2=0 (d) none of these
View SolutionThe coordinates of a particle moving in x-y plane at any time t are Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
View SolutionThe coordinates of a particle moving in x-y plane at any time t are (2 t, t^2). Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
View Solutionचित्र में एक कण के x -निर्देशांक का समय के साथ संबंध बताया गया है । के चिह्न पर क्या होंगे ?
View SolutionFigure shows x-t graph of a particle. Find the Time T Such that the Average Velocity of the Particle During the Period 0 to T is Zero..
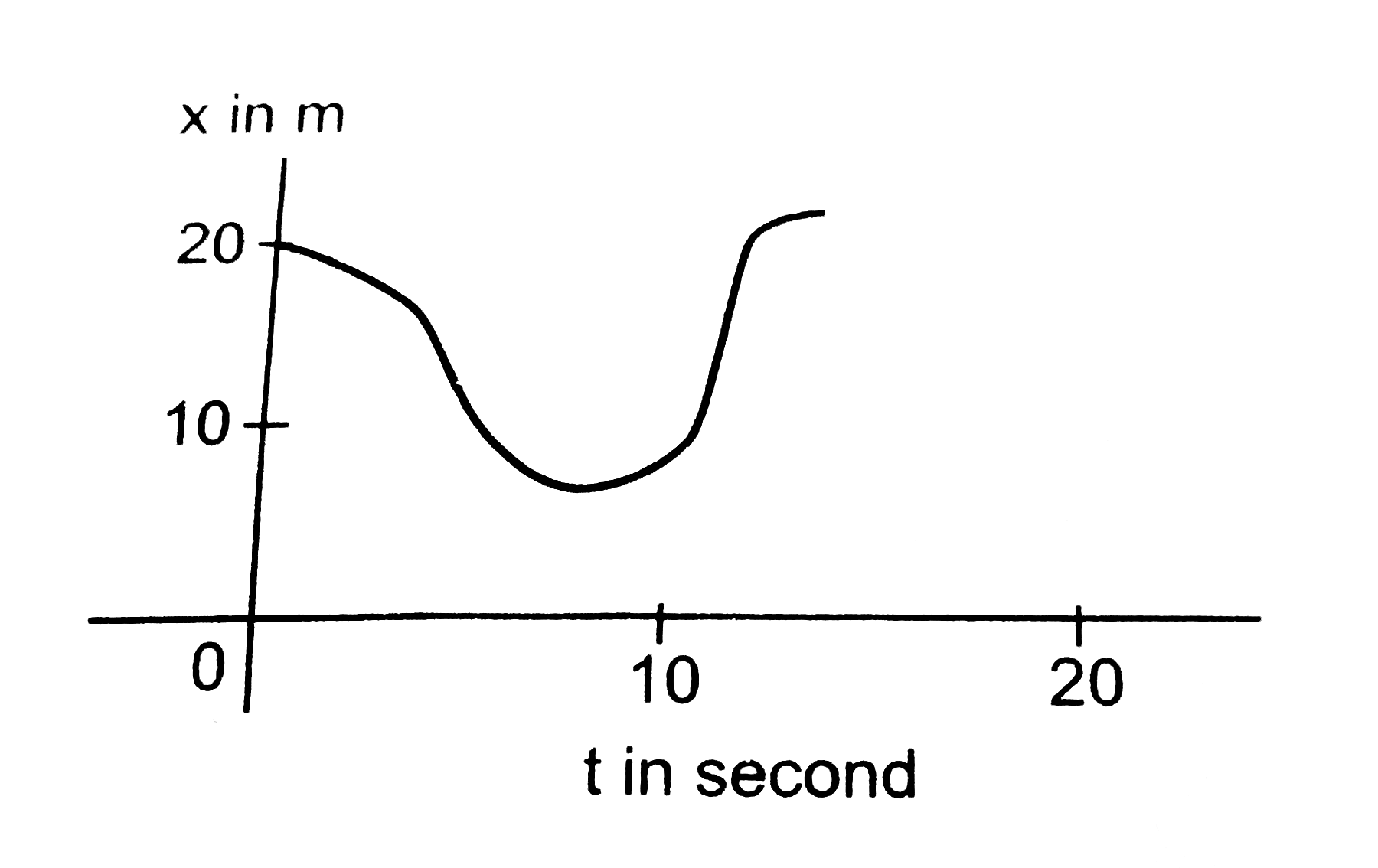
View SolutionFigure shows x-t graph of a particle. Find the Time T such that the average velocity of the particle during the period 0 to T is Zero.
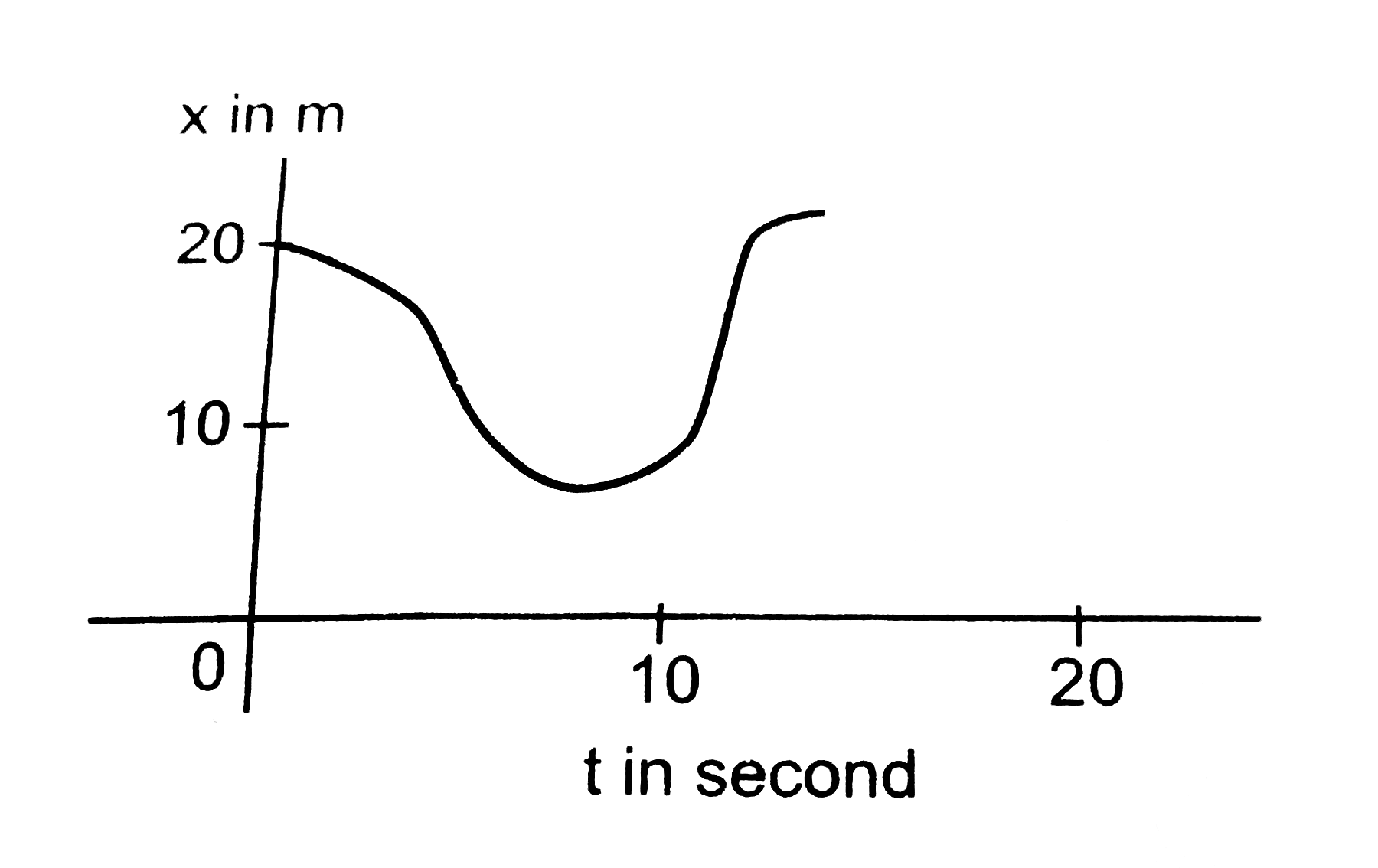
View SolutionFigure shows x-t graph of a particle. Find the Time T such that the average velocity of the particle during the period 0 to T is Zero.
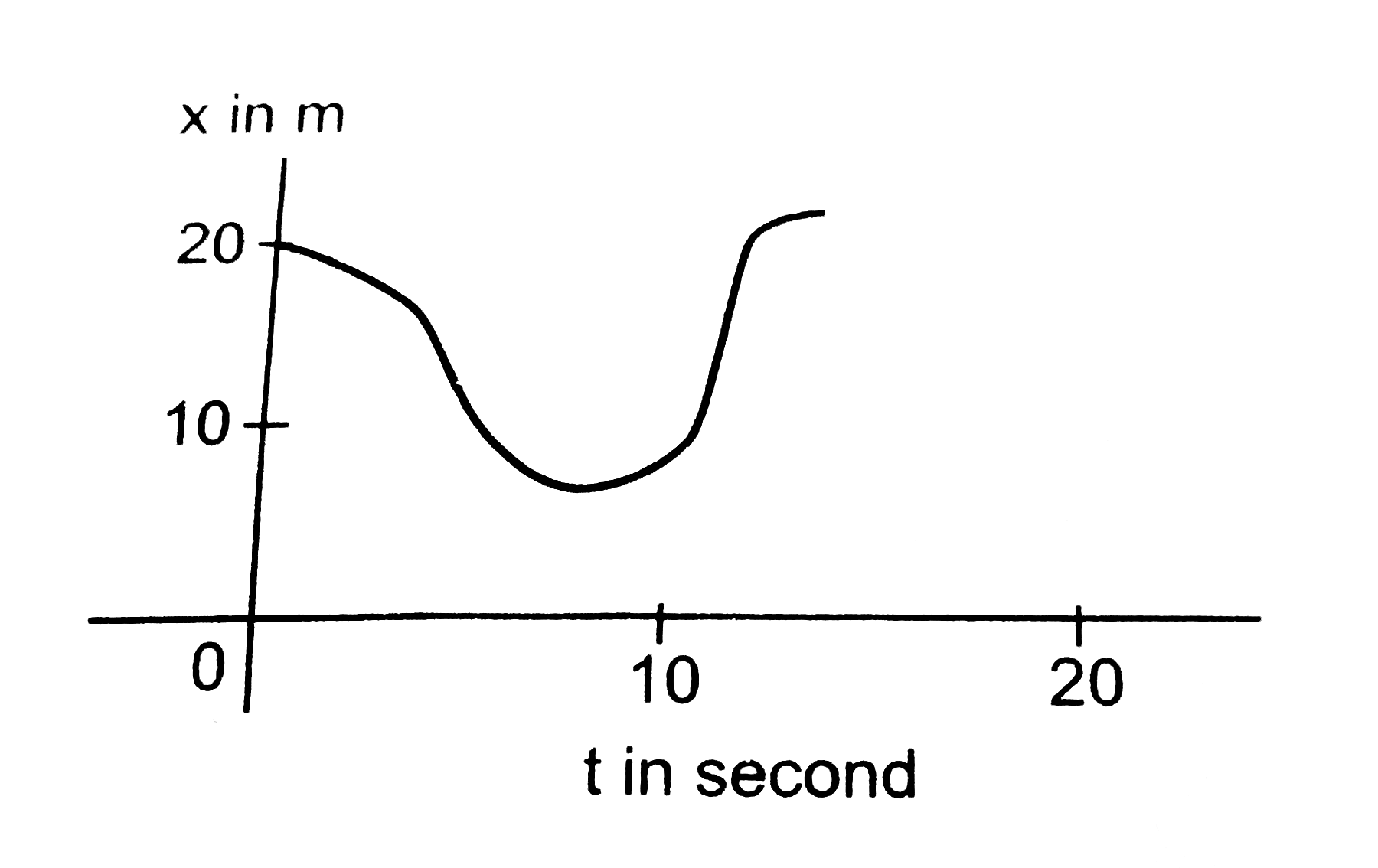
View Solution