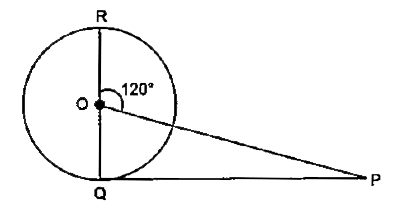
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR =120o then find ∠OPQ.
∠QOP + ∠POR = 180°∠QOP + 120° = 180°∠QOP = 180° - 120°∠QOP = 60°In ΔPOQ∠QOP + ∠OPQ + ∠PQO = 180°60° + ∠OPQ + 90° = 180°150° + ∠OPQ = 180°∠OPQ = 180° - 150°∠OPQ = 30°
Related Solutions
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that . Find .
View SolutionPQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that . Find .
View SolutionO - வை மையமாக உடைய வட்டத்திற்கு P -யிலிருந்து வரையப்பட்ட தொடுகோடு PQ .QOR ஆனது விட்டம் ஆகும் .வட்டத்தில் POR = எனில் ,OPQ -ஐக் காண்க ?
View SolutionPQ is a tangent drawn from an external point P to a circle with center O, is the diameter of the circle. If . What is the measure of ?
View Solutionकेंद्र वाले वृत्त पर बिंदु से स्पर्श रेखा खींची गई हैं और वृत्त का एक व्यास इस तरह हैं की , तब हैं.।
View Solutionis a tangent drawn from a point to a circle with centre and is a diameter of the circle such that , then is (b) (c) (d)
View SolutionO is the centre of the circle QOR is diameter. PQ is tangent to the circle. Given . Find .
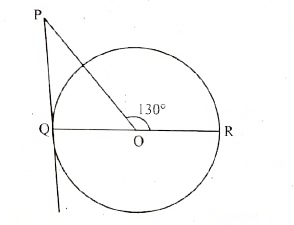
View SolutionPQ is tangent drawn from point P to a circle with centre O and QR is a diameter of the circle, such that . Then, .
View SolutionIf two tangents are inclined at are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If OPQ is an isosceles triangle, then find OQP.
View SolutionIn the figure , PQ and PR are the tangents drawn form P to a circle with centre O. if then
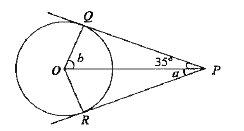
View SolutionIn Fig,PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter.If /_POR=130^(@) and S is a point on the circle, find /_1+/_2
View SolutionA point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then is
View SolutionFrom a point , two tangents and are drawn to a circle with centre . If diameter of the circle, show that is equilateral.
View SolutionTwo tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If then find .
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If angleTPQ=70^(@) , find angleTRQ .
View SolutionIn the background O Is the center of the circle. PQ Is the tangent line of the circle and P Touch is the point. angle OPQ What is the value of?
View SolutionA point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm. Find the length of OR.
View SolutionA point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm. Find the length of PR.
View SolutionO is the centre of a circle. An external point P is 26 cm away from the centre of the circle and the length of the tangent (PT) drawn from the point P to the circle at T is 10 cm. Calculate the length of the diameter of the circle.
View Solution