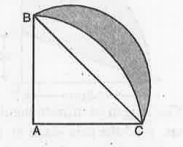
Doorway is decorated as shown in the figure. There are four semi-circles. BC the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semi-circles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC find the area of the shaded region. Take π = 22/7.
As angle in a semi circle is 90° Diameter of each of three equal semicircles=1/3 x 84 =28 cmRadius of each of 3 equal semicircles = 14 cmArea of the shaded region= Area of semicircle with 42 cm as Radius + Area of three equal semi- circles of radius 14 cm- area of Δ ABC
Related Solutions
ABC is an isosceles right angled triangle with . A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. (Take )

View SolutionIn the figure, ABC is in the semi-circle, find the area of the shaded region given that AB = BC =4 cm.
View SolutionIn fig., ABC is a quadrant of a circle of radius 14 cm and a semi circle is drawn with BC as diameter. Find the area of the shaded region.
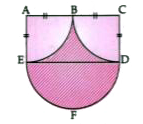
View SolutionFind the perimeter and area of shaded region where ADC, AEB and BFC are semi-circles on the diameter AC, AB and BC respectively. ( pi=22/7 )
View SolutionIn the figure, ABC is in the semi-circle, find the area of the shaded region given that AB = BC =4 cm
View SolutionIn the figure, is in the semi-circle, find the area of the shaded region given that AB = BC = 4 cm. (use )

View SolutionCalculate the area of the shaded region, if the diameter of the semi-circle is equal to 14 cm.
(Take )
View SolutionIn the given figure, AB is the diameter of the largest semi-circle. AB = 21 cm, AM = MN = NB. Semi-circles are drawn with AM, MN and NB as shown. Using , calculate the area of the shaded region.
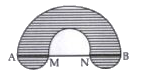
View SolutionIn the given figure, AB is the diameter of the largest semi-circle. AB =21 cm, AM = MN = NB. Semi-circles are drawn with AM, MN and NB as shown. Using , calculate the area of the shaded region.

View SolutionIn the following figure AB=BC and AC=84 cm. The radius of the inscribed circle is 14 cm. B is the centre of the largest semi-circle . What is the area of the shaded region ?
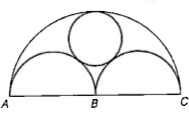
View SolutionIn figure ABDC is a quadrant of a circle of a radius 28 cm and a semi circles BEC is drawn with BC as diameter find the area of shaded region:
View SolutionIn the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semi circles are drawn with AD and BC as diameters. Find the area of the shaded region
(Take )
View SolutionA right angled isosceles triangle is inscribed in a semi-circle of radius 7 cm. The area enclosed by the semi-circle but exterior to the triangle is
View SolutionIn Figure AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.
View SolutionCircle inside a Circle : PQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal. Semi circles are drawn on PQ and QS as diameters, as shown in Figure. Find the perimeter and area of shaded Region.
View SolutionA semi-circle of diameter 1 unit sits at the top of a semi-circle of diameter2 units. The shaded region inside the smaller semi-cricle but outside the larger semi-circle a lune. The area of the lune is-

View SolutionIn fig ABC is a right angled triangle in which /_A=90^(@),AB=21 cm and AC=28cm Semi- circles are described on AB,BC and AC as diameters.Find the area of the shaded region
View SolutionThe largest triangle is inscribed in a semi-circle of radius 7 cm. Find the area inside the semi-circle which is not occupied by triangle.
View SolutionIn the figure APB and AQB are semi-circles and . If the perimeter of the figure is , find the area of the shaded region.
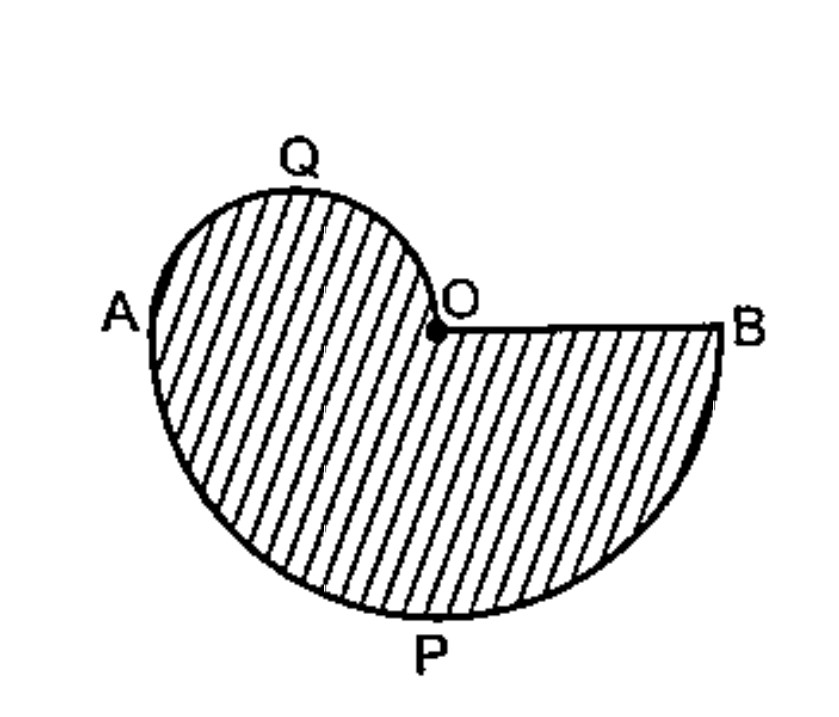
View SolutionPQRS is the diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semi-circles are drawn with PQ and QS as diameters as shown in the figure alongside. Find the ratio of the area of the shaded region to that of the unshaded region.
View Solution