Match the conditions/expressions in Column I with statement in Column II.Normal at P Q R are drawn to y2 = 4x which intersect at 3 0. ThenColumn IColumn IIA Area of ΔPQRp 2B Radius of circumcircle of ΔPQRq 5/2C Centroid of ΔPQRr 5/2 0D Circumcentre of ΔPQRs 2/3 0
A→pB→qC→sD→rExplanation:Since equation of normal to the parabola y2 = 4x is y + xt = 2at + at3 passing through 3 0
Related Solutions
Match the conditions/expression in Column I With statement in Column II. Normals at P,Q,R are drawn to which intersect at (3,0). Then,
View Solutionपरवलय पर स्थित बिन्दुओं P,Q तथा R से अभिलंब खींचे जाते है जो कि (3,0) पर प्रतिच्छेद करते है। तब, कॉलम I में दी गयी स्थितियों/व्यंजकों का कॉलम ॥ में दिए गए वक्तव्यों से सुमेल करें:

View SolutionNormals at P, Q, R are drawn to which intersect at (3, 0). Then, area of , is
View SolutionNormals at P, Q, R are drawn to which intersect at (3, 0). Then, area of , is
View SolutionNormals at P, Q, R are drawn to which intersect at (3, 0). Then, area of , is
View SolutionNormals are drawn at points P, Q are R lying on the parabola which intersect at (3, 0), then

View SolutionMatch the conditions /expression n Column I with statement in Column II is a complex number )

View SolutionMatch the conditions/expressions in Column I with values in Column II
is
View SolutionMatch the conditions/expressions in Column I with values in Column II
is
View SolutionMatch the conditions/ expressions in Column I with statement in Column II
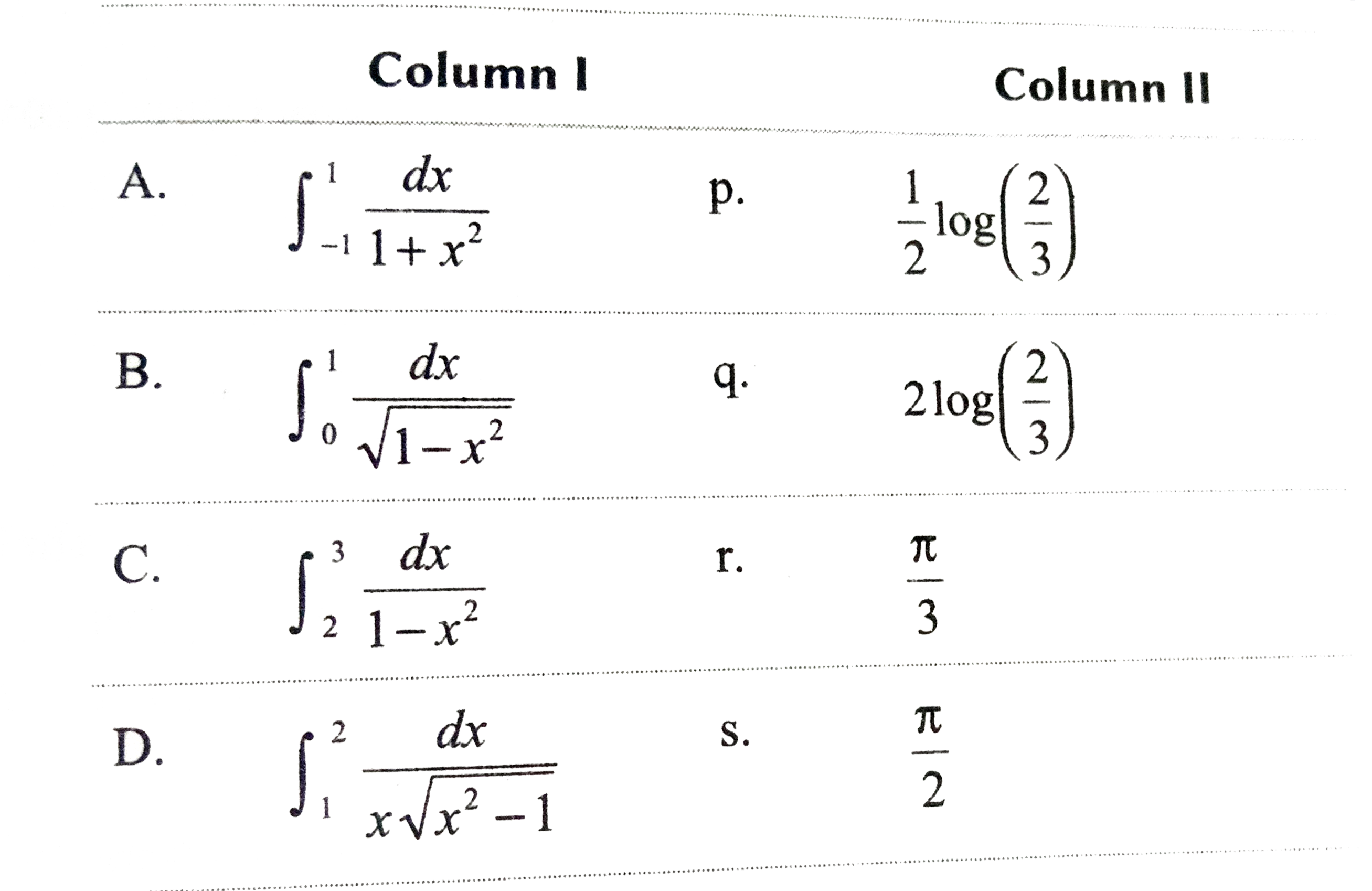
View SolutionMatch the conditions expression in Column I with statement in Column II.
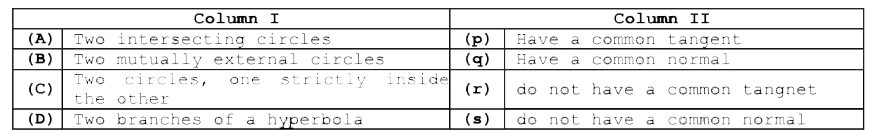
View SolutionMatch the conditions/ expressions in Column I with statement in Column II

View SolutionMatch the conditions expression in Column I with statement in Column II.
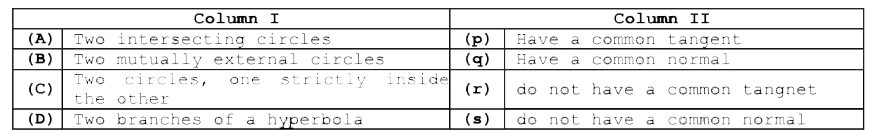
View SolutionMatch the conditions/ expressions in Column I with statement in Column II

View SolutionColumn I, Column II Points from which perpendicular tangents can be drawn to the parabola , p. Points from which only one normal can be drawn to the parabola , q. (3, 2) Point at which chord of the parabola is bisected., r. Points from which tangents cannot be drawn to the parabola , s.
View SolutionColumn I, Column II Points from which perpendicular tangents can be drawn to the parabola , p. Points from which only one normal can be drawn to the parabola , q. (3, 2) Point at which chord of the parabola is bisected., r. Points from which tangents cannot be drawn to the parabola , s.
View SolutionColumn I, Column II Points from which perpendicular tangents can be drawn to the parabola y^2=4x , p. (-1,2) Points from which only one normal can be drawn to the parabola y^2=4x , q. (3, 2) Point at which chord x-y-1=0 of the parabola y^2=4x is bisected., r. (-1,-5) Points from which tangents cannot be drawn to the parabola y^2=4x , s. (5,-2)
View Solution58. Match the column Column t Column-II The value of k for which x +y4 P 2/5 I and x+ y-2x+ 2ky k cut 11 | 4y = 3x + 1 on the circle 111 | 2x-ky + 3 = 0, 4x + y + 5 = 0 cut orthogonally The length of the chord cut by e -8 x2 + y2-6x = 0 The value of k for which lines R 4.5 axes in concyclic point In any triangle, the maximum value IV 123 must be S -4 of R C) I-S; II-P; II-R; IV-Q PII-S; II-P; IIL-Q; IV-R
View SolutionLet Match the expressions/ statements in Column I with expressions / Statement in column II.
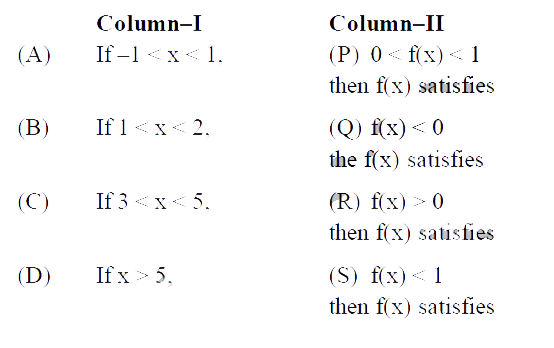
View Solutionconsider the ellipse and match column I to column II according to the given condition.

View Solution