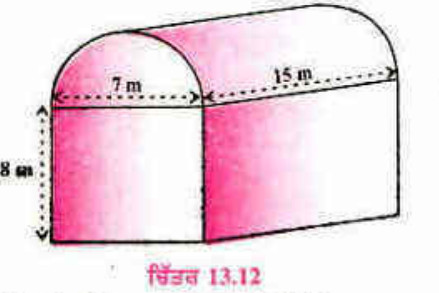
Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder see Fig. 13.12. If the base of the shed is of dimension 7 m × 15 m and the height of the cuboidal portion is 8 m find the volume of air that the shed can hold. Further suppose the machinery in the shed occupies a total space of 300 m3 and there are 20 workers each of whom occupy about 0.08 m3 space on an average. Then how much air is in the shed? Take π=22/7
The volume of air inside the shed when there are no people or machinery is given by the volume of air inside the cuboid and inside the half cylinder taken together.Now the length breadth and height of the cuboid are 15 m 7 m and 8 m respectively.Also the diameter of the half cylinder is 7 m and its height is 15 m.So the required volume = volume of the cuboid +1/2 volume of the cylinderNext the total space occupied by the machinery = 300 m3And the total space occupied by the workers = 20 × 0.08 m3 = 1.6 m3Therefore the volume of the air when there are machinery and workers= 1128.75 – 300.00 + 1.60 = 827.15 m3
Related Solutions
Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder. If the base of the shed is of dimension , and the height of the cuboidal portion is 8 m, find the volume of the air that the shed can hold. If the industry requires machinery which would occupy a total space of , and there are 20 workers each of whom would occupy space on an average, how much air would be in the shed when it is working. (Take )
View SolutionShanta runs an industry in a shed which isin the shape of a cuboid surmounted by a half cylinder (see the given figure). If the base of the shed is of dimension , and the hegiht of the coboidal portion is 8m find the volume of air that the shed can hold. Further suppose te machinery in the shed occupies a total space of , and there are 20 workers, each of whom occupy about space on an average . Then how much air is in the shed ? (Take

View SolutionShanta runs an industry in a shed which is in the shape of a cuboidsurmounted by a half cylinder. If the base of the shed is of dimension , and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold.Further suppose the machinery in the shed occupies 300 and 20 workers each of whom occupy 0.08 space on an average.Then how much air is in the shed.
View SolutionShanta runs an industry in a shed which is in the shape of a cuboidsurmounted by a half cylinder. If the base of the shed is of dimension , and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold.Further suppose the machinery in the shed occupies 300 and 20 workers each of whom occupy 0.08 space on an average.Then how much air is in the shed.
View Solutionਸ਼ਾਂਤੀ ਕਿਸੇ ਸ਼ੈੱਡ ਵਿੱਚ ਇੱਕ ਉਦਯੋਗ ਚਲਾਉਂਦੀ ਹੈ।ਇਹ ਸ਼ੈੱਡ ਇੱਕ ਘਣਾਵ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸਦੇ ਉਪਰ ਇਕ ਅਰਧ ਵੇਲਣ ਬਣਿਆ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 13.12)। ਜੇਕਰ ਇਸ ਸੈੱਡ ਦੇ ਆਧਾਰ ਦੀਆਂ ਪਸਾਰਾਂ 7m x 15 m ਹਨ ਅਤੇ ਘਣਾਵ ਆਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ 8m ਹੈ ਤਾਂ ਸੈੱਡ ਵਿੱਚ ਮੌਜੂਦ ਹਵਾ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੇ। ਹੁਣ ਜੇਕਰ ਇਹ ਮੰਨ ਲਈਏ ਕਿ ਸੈੱਡ ਵਿੱਚ ਰੱਖੀ ਮਸ਼ੀਨਰੀ 300 ਸਥਾਨ ਘੇਰਦੀ ਹੈ ਅਤੇ ਸ਼ੈੱਡ ਦੇ ਅੰਦਰ 20 ਮਜਦੂਰ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਹਰੇਕ 0.08 ਦੇ ਔਸਤ ਨਾਲ ਸਥਾਨ ਘੇਰਦਾ ਹੈ ਤਾ ਸੈੱਡ ਵਿੱਚ ਕਿੰਨੀ ਹਵਾ ਹੋਵੇਗੀ? ( ਲਓ।)
View SolutionA shed consists of a cuboid surmounted by half cylinder,as shown in the figure.If the base of the shed is 7m xx15m and height of the cuboidal part is 8m ,find the volume of air contained in the shed.Also,find the internal surface area excluding the floor.
View Solutionशांता किसी शेड में एक उद्योग चलती है | यह शेड एक घनाभ के आकर का है जिस पर एक अर्थ बेलन आरोपित है | यदि इस शैड के आधार की विमाएँ है तथा घनभाकार भाग की ऊँचाई 8 मी. है तो 300 घन मीटर स्थान घेरती है तथा शेड के अंदर 20 श्रमिक है जिनमे से प्रत्येक घन मीटर के औसत से स्थान घेरता है तब सेड में कितनी हवा होगी ?
View SolutionThere si a closed rectangular shed of shed of dimensions inside a field. A cow is tied at one corner of outside of the shed with a 6 m long rope. What is the area that the cow can graze in the field?
View SolutionABCDE is the end view of a factory shed which is 50m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
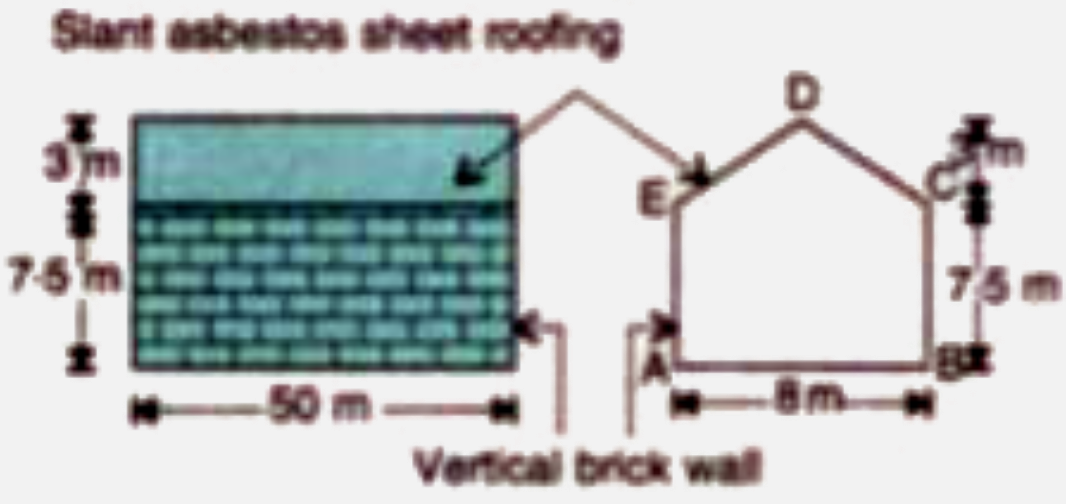
Calculate the total volume content of the shed
View SolutionA closed rectangular shed has dimensions 21m14m. It is inside a field.A cow is tied outside the shed at one of its corners with a 21 m rope.Find the area over which the cow can graze (in m^(2))
View SolutionDwarf shoot in Pinus is Shed every year Shed after 2-3 years Shed after five years Never shed.
View SolutionABCDE is the end view of a factory shed which is 50m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
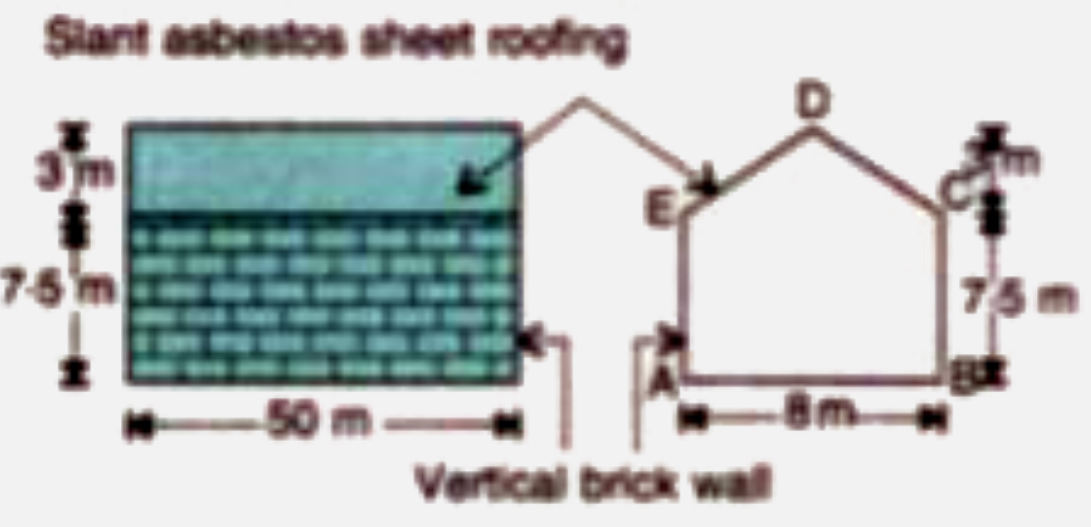
If the whole outside surface of the shed (including roofing) is to be painted, find the cost of painting it at Rs 5 per (sq.metre).
View SolutionA closed rectangular shed has dimensions 21 m 14 m. It is inside a field. A cow is tied outside the shed at one of its corners with a 21 m rope. Find the area over which the cow can graze (in ).
View SolutionEcdysis is shedding of
View SolutionThe shed is located:
View SolutionThe shed is located:
View SolutionThe poem “The Shed’ is a:
View SolutionWhat is shedding?
View SolutionEcdysis is shedding of
View SolutionWhich creature sheds light?
View Solution