Find the eccentricity of the central conic section ax2 + 2hxy + by2 = 1
ax2 + 2hxy + by2 = 1 ......1Let h2 - ab be negative so that the curve is an ellipse and let the equation to the ellipse referred to its axes beBy the theory of invariants we haveAlso if e be the eccentricity we have if α be > β But from 2 and 3 we haveThis equation at once gives e2.
Related Solutions
Find the equation to the conic section whose focus is (1, -1), eccentricity is and the directrix is the line . Is the conic section an ellipse?
View SolutionThe directrix of a conic section is the line and the focus S is (-2, 3). If the eccentricity e is , find the equation to the conic section.
View SolutionFind the equation the conic whose focus is eccentricity is and the directrix is the line Is the conic section an ellipse ?
View SolutionIf for a conic section a focus is (-1,1), eccentricity=3 and the equation of the corresponding directrix is x-y+3=0, then the equation of this conic section is
View SolutionThe equation of conic section whose focus is at (-1 , 0), directrix is the 4x-3y+2=0 and eccentricity 1, is
View SolutionThe equation of conic section whose focus is at (-1 , 0), directrix is the and eccentricity , is
View SolutionConic Section: Lecture 1
View SolutionConic Section: Lecture 1
View SolutionThe eccentricity of the conic is
View SolutionThe eccentricity of the conic x ^(2) -4y ^(2) =1 is
View SolutionThe eccentricity of the conic is
View SolutionFind the condition for the line y= mx to cut at right angles the conic
View SolutionFind the condition for the line to cut at right angles the conic
View SolutionLet y = mx and be the lines represented by the equation ax2+2hxy+by+=0. Match the following and choose the correct answer.
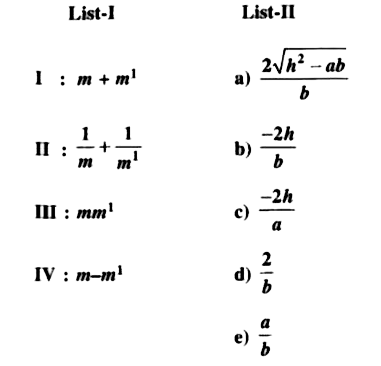
View SolutionConsider the conic
find the eccentricity.
View SolutionIf and are the eccentricities of two conics with , then the conics are
View SolutionThe eccentricity of the conic section represented by is
View SolutionEquation , represent a conic section whose eccentricity e is given by
View SolutionThe coordinates of a point are where is a parameter , then the point lies on a conic section whose eccentricity is
View SolutionConic Sections
View Solution