If E and F are events such that PE/F = PF/E then which is the following is true ? A PE = PF B E = F C E ⊂ F but E ≠ F D E ∩ F = ϕ
Related Solutions
If then
View SolutionIn Figure, and . Prove that .
View Solutiona d c e b e d f e h e ?
View SolutionIf and are independent events such that and then (a) are mutually exclusive (b) (the complement of the event ) are independent (c) are independent (d)
View SolutionIf in two triangles and , , then (b) (c) (d)
View SolutionIf in two triangles and , , then (b) (c) (d)
View SolutionIf are the complementary events of events respectively, and if then b. c. d.
View SolutionIn Figure, .If then is congruent to:
(a)
(b)
(c)
(d)
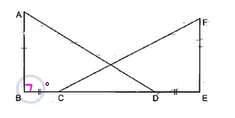
View SolutionIn Figure, If then is congruent to: (b) (c) (d)
View SolutionIf and are two triangles such that , then
View SolutionIf E and F are any two events such that P(E) + P(F) - P(E and F) = P(E) Then (A) P(F/E) = 1 , (B) P(E/F) = 1 , (C) P(F/E) = 0 , (D) P(E/F) = 0.
View SolutionIf and are two triangles such that , then write Area .
View Solutionমনে করো, এবং চিত্রণ নিম্নরূপে সংজ্ঞাত: এবং নির্ণয় করো
View SolutionIn Fig. if Prove that . (FIGURE)
View SolutionIn Fig. if Prove that . (FIGURE)
View SolutionLet R be a relation such that R={(a ,c), (c ,g) ,(d ,e), (d, f) ,(g, f)} then is
View SolutionLet R be a relation such that R={(a d) (c g) (d e) (d f) (g f)} then (R@R^(-1))^(-1) is qquad {(d d) (g g) (e e) (f f) (e f) (f e)} O{(e a) (f a) (f c)} O{(a e) (a f) (c f) O{(d d) (g g) (e e) (f f) (e f)}
View SolutionLet R be a relation such that R={(a d) (c g) ) (d e) (d f) (g f)} then (R R^(-1))^(-1) is {(d d) (g g) (e e) (f f) (e f) (f e)} {(e a) (f a) (f c)} {(a e) (a f) (c f) {(d d) (g g) (e e) (f f) (e f)}
View SolutionLet R be a relation such that R={(a d) (c g) (d e) (d f) (g f)} then (R@R^(-1))^(-1) is qquad {(d d) (g g) (e e) (f f) (e f) (f e)} O{(e a) (f a) (f c)} O{(a e) (a f) (c f) O{(d d) (g g) (e e) (f f) (e f)}
View SolutionIf E and F events with and , then (a) occurrence of E occurrence of F(b) occurrence of F occurrence of E (c) non-occurrence of E non-occurrence of F(d) none of the above implications hold
View Solution