If the tangents at P and Q meet in T prove that1 TP and TQ subtend equal angles at the focus S2 ST2 = SP.SQ and 3 the triangles SPT and STQ are similar.
Let P be the point at2 2at1 and Q be the point at22 2at2 so that T is the point {at1t2 at1 + t2}.The perpendicular TU from T on this straight lineSimilarly TU has the same numerical value.The angles PST and QST are therefore equal.and the angles TSP and TSQ are equal the triangles SPT and STQ are similar so that
Related Solutions
TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q' . Prove that (TP')/(TP)+(TQ')/(TQ)=1
View SolutionTP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q'. Prove that (TP')/(TP)+(TQ')/(TQ)=1
View SolutionTP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q' . Prove that (TP')/(TP)+(TQ')/(TQ)=1
View Solutionand are any two tangents to a parabola and the tangent at a third point cuts them in and . Prove that
View Solutionand are any two tangents to a parabola and the tangent at a third point cuts them in and . Prove that
View SolutionIf the distances of two points P and Q on the parabola from the focus of a parabola are 4 and 9 respectively then the distance of the point of intersection of tangents at P and Q from the focus is
View SolutionIf the tangents at the points on the parabola meet at is its focus, prove that .
View SolutionIf the tangents at the points on the parabola meet at is its focus, prove that .
View SolutionThe tangents to the parabola at the vertex and any point meet at . If is the focus, then prove that and are in GP.
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that , then is equal to
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that .
View SolutionTwo parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
View SolutionTP&TQ are tangents to the parabola,y^(2)=4ax at P and Q. If the chord passes through the point (-a,b) then the locus of T is
View SolutionTP तथा TQ परवलय कि स्पर्श रेखाएं है और P व Q पर अभिलम्ब, वक्र को बिन्दु R पर मिलते है। सिद्ध कीजिए कि त्रिभुज TPQ के परिगत वृत्त का केन्द्र परवलय पर स्थित है।
View SolutionConsider the curve Tangents and are drawn on at and Also normals at and meet at The coordinates of circumcentre of is
View SolutionTwo tangents TP and TQ are drawn to a circle with centre 'O' from on external point T. Prove that
= .
View SolutionTwo tangent TP and TQ are drawn to a circle with centre O from an external point T. prove that PTQ=2OPQ.
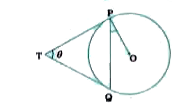
View Solutionकेंद्र O वाले वृत्त पर बाह्य बिंदु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं। सिद्ध कीजिए की है ।
View SolutionTP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
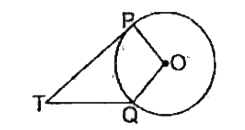
View SolutionIf two tangent TP and TQ are drawn from an external point T such that then find .
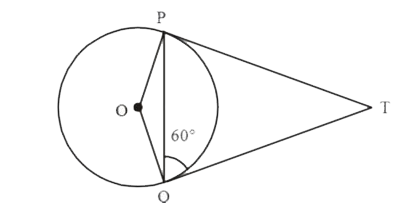
View Solution