Two rigidly connected homogeneous rods of the same length and mass m1 and m2 respectively form an angle pi/2 and rest on a rough horizontal surface Fig. 23. The system is uniformly pulled with the help of a string fixed to the vertex of the angle and parallel to the surface.Determine the angle a formed by the string and the rod of mass m1.
After the translatory motion of the system has been established the ratio of the forces of friction Ffr1 and Ffr2 acting on the first and second rods will be equal to the ratio of the forces of pressure of the corresponding regions: Ffr1/Ffr2 = N1/N2. Since each force of pressure is proportional to the mass N1 = m1g and N2 = m2g the ratio of the forces of friction can be written in the formOn the other band from the equality of the moments of these forces about the vertex of the right angle Fig. 158 top view we obtainwhere l is the distance from the vertex to the centres of mass of the rods. From Eqs. 1 and 2 we obtainConsequently
Related Solutions
Two rigidly connected homogeneous rods of the same length and mass m_(1) and m_(2) respectively form an angle pi//2 and rest on a rough horizontal surface (Fig.) The system is uniformly pulled with the help of a string fixed to the vertex of the angle and parallel to the surface. Determine the angle alpha formed by the string and the rod of mass m_(1) .
View SolutionA smooth ring of mass connected with a hanging block of mass by a long inextensible string, is released from rest. The ring moves vertically along a fixed rigid rod as shown in figure. Describe the motion of the ring if
(A)
(B)
(C )
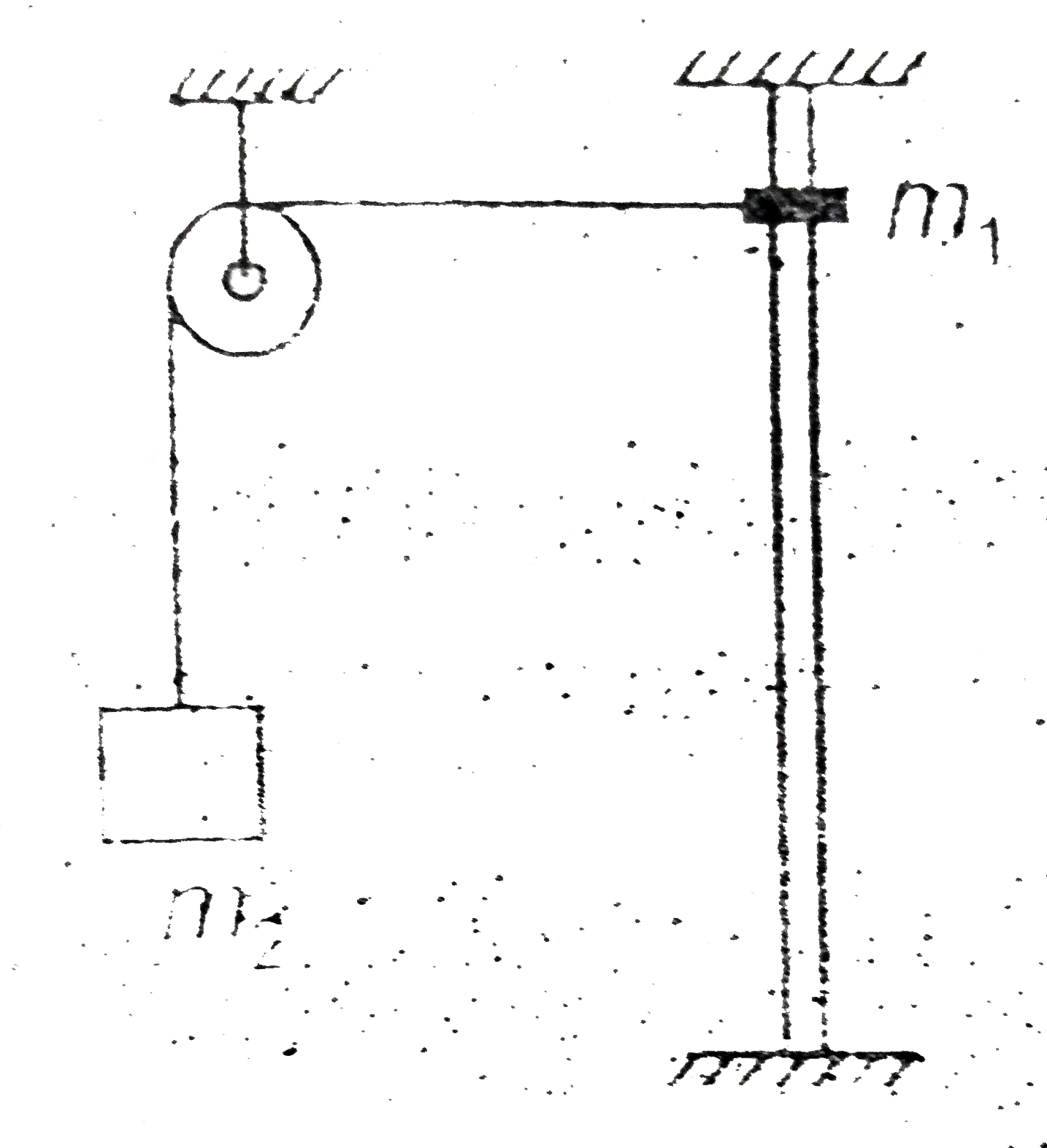
View SolutionA straight metal rod of length is bend through the righ angle as shown. The bend rod is then placed on a rough horizontal table. A ligh string is attached to the vertex of the right angle. The string is then pulled horizontally so that the rod slides at a constant velocity. Find the angle that side would make with the string.
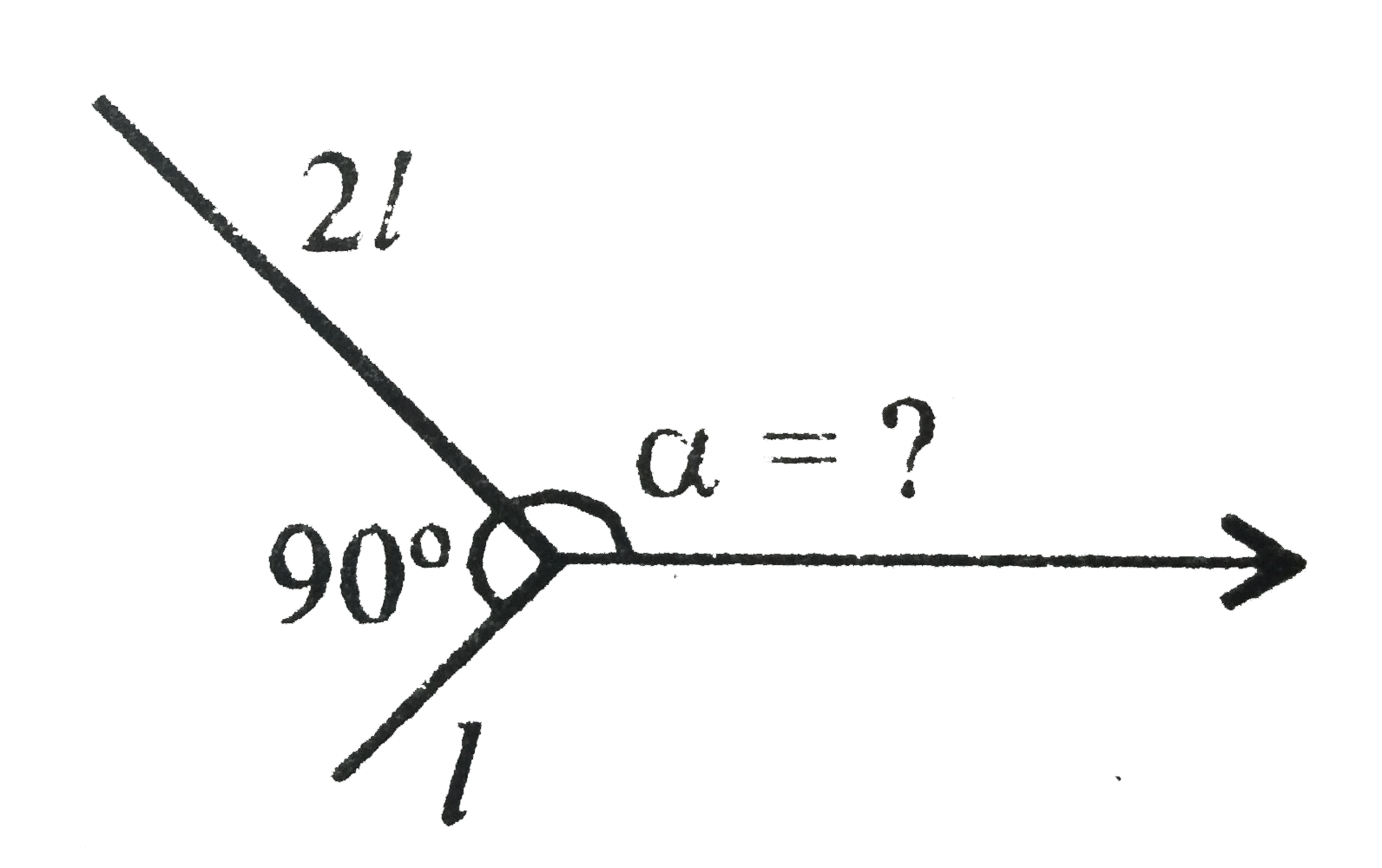 .
.
View SolutionTwo masses m1 and m2 are connected by light string, which passes over the top of a smooth plane inclined at 30º to the horizontal, so that one mass rests on the plane and the other hangs vertically as shown in fig. It is found that m1, hanging vertically can draw m2 up the full length of the plane in half the time in which m2 hanging vertically draws m1 up. Find m1/m2 . Assume pulley to be smooth-

View SolutionTwo plane mirrors M1 and M2 , placed at right angles, form two sides of a container. Mirror M1 is inclined at an angle theta_(0) to the horizontal. A light ray AB is incident normally on M1 . Now the container is filled with a liquid of refractive index mu so that the ray is first refracted, then reflected at M1 . The ray is next reflected at M2 and then comes out of the liquid surface making an angle theta with the normal to the liquid surface. Find theta .
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionIn Fig. a massive rod AB is held in horizontal position by two massless strings. If the string at B breaks and if the horizontal acceleration of centre of mass, vertical acceleration and angular acceleration of rod about the centre of mass are a_x,a_y respectively, then
View SolutionTwo small rings each of mass are connected to a block of same mass through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings make an angle of with vertical is. (Take )

View SolutionA thin uniformed rod of mass and length is hinged at one end and from other end a light string is attached. The string is wound over a frictionless pullely (having mass ) and a block of mass is connected to string on other side of pulley as shown. the system is released from rest when the rod id making an angle of with horizontal. Based on above information answer the following question :
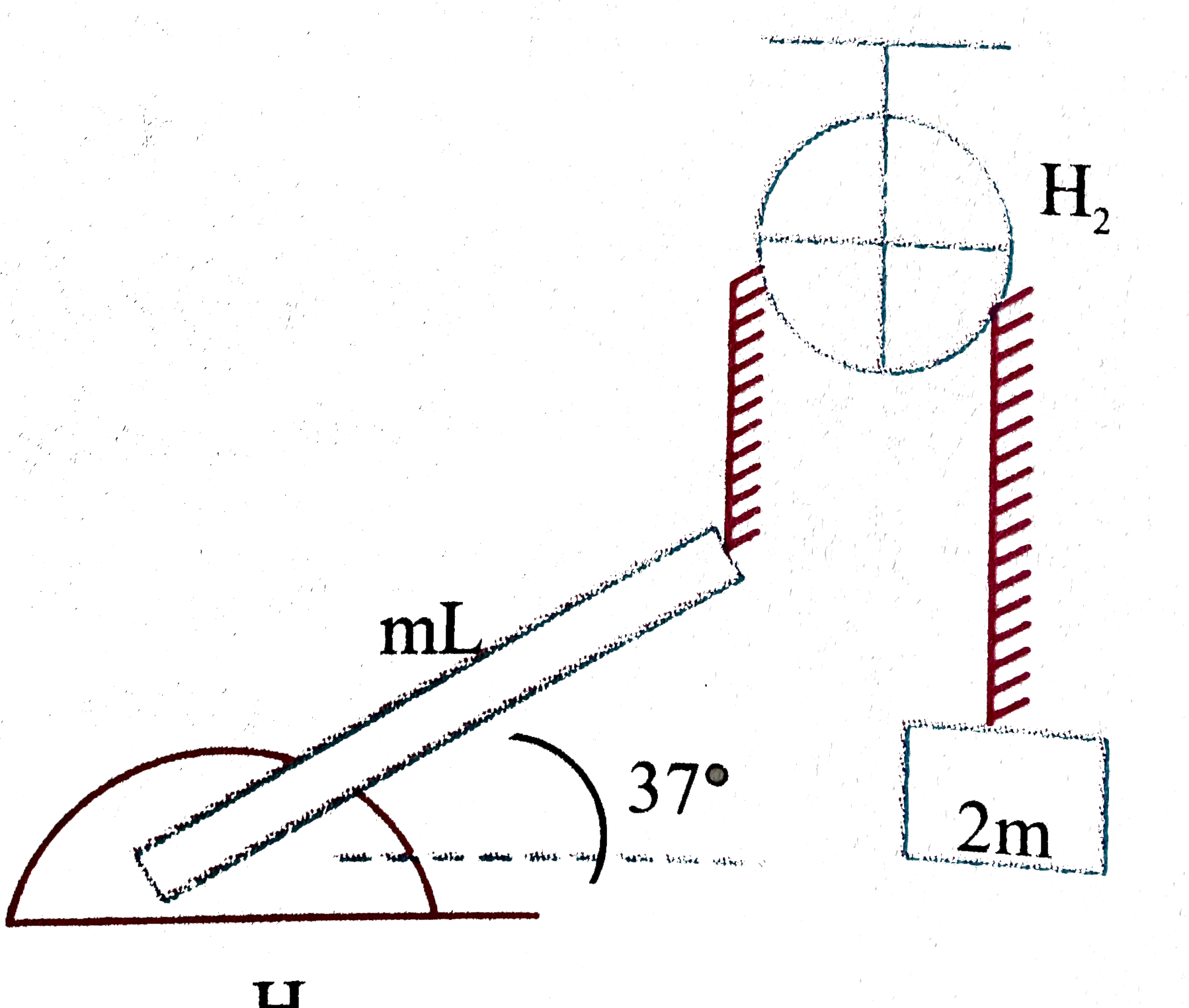
Just after releases of the system from rest acceleration of block is
View SolutionTwo spherical balls of masses m1 and m2 collide as shown in figure. After collision mass m1 moves with velocity u/3 in a direction perpendicular to original direction. The angle at which mass m2 will move after collision is
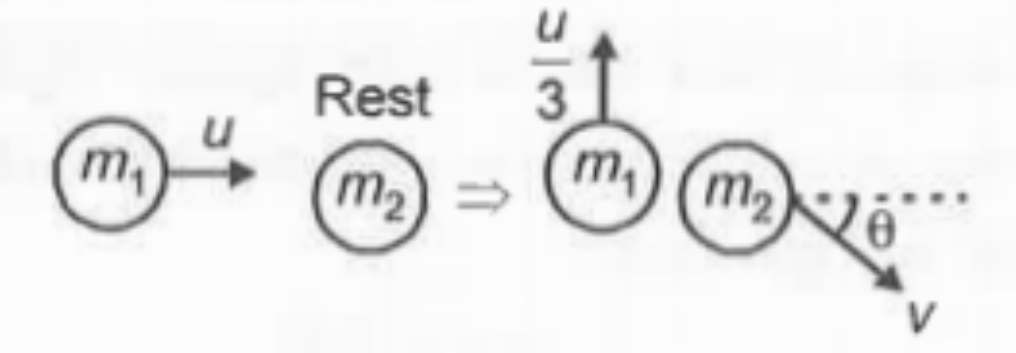
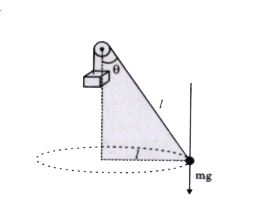
View SolutionThe figure shows a rod arranged at an angle of from the horizontal. Two strings are fixed to rod as shown. Attached to the two strings is the mass as shown. The rod is rotated maintaining its direction in space, so that travels in a circular path. The strings are of equal length and make angle of with the rod as shown. Calculate the minimum value of the tangential speed of the mass such that the string with tension does not become slack when the mass is directly aboye the rod. Take length of string as.
'(##CEN_KSR_PHY_JEE_C07_036_Q22##)'
View SolutionA large free mass M and a small mass m are connected to a string such that m moves in horizontal circle Length of string is I and is the angle this length makes with vertical. The frequency of rotation of mass m that M remains at rest is
View SolutionTwo blocks connected by a massless string slide down an inclined plane having angle of inclination 37º. The masses of the two blocks are M1 = 4 kg and M2 = 2 kg respectively and the coefficients of friction 0.75 and 0.25 respectively- The common acceleration of the two masses is 1.3 ms^(-2) b, The tension in the string is 14.7 N c The common acceleration of the two masses is 2.94 ms^(-2) d, The tension in the string is 5.29N
View Solution
Two blocks of masses and connected by a string are placed gently over a fixed inclined plane, such that the tension in the connecting string is initially zero. The coefficient of friction between and inclined plane is , between and the inclined plane is . The tension in the string shall continue to remain zero if
View SolutionA partical of mass m1 is travelling with avelocity u1 strikes head-on against partical of mass m2 at rest.After collision the particales move with a velocity v1 and v2 respectively .show that the ratio of decrese in K.E of the partical of mass m1 to its original K.E is given By (4m1m2)/(m1+m2)^2
View SolutionA L shaped, uniform rod has its two arms of length l and 2l . It is placed on a horizontal table and a string is tied at the bend. The string is pulled horizontally so that the rod slides with constant speed. Find the angle theta that the longer side makes with the string. Assume that the rod exerts uniform pressure at all points on the table.
View SolutionTwo masses are connected by a light rod and the system is slipping down a rough incline of angle with the horizontal. The friction coefficient at both the contacts is . Find the acceleration of the system, and the force by the rod on one of the blocks.
View SolutionTwo masses are connected by a light rod and the system is slipping down a rough incline of angle with the horizontal. The friction coefficient at both the contacts is . Find the acceleration of the system, and the force by the rod on one of the blocks.
View SolutionTwo masses are connected by a light rod and the system is slipping down a rough incline of angle with the horizontal. The friction coefficient at both the contacts is . Find the acceleration of the system, and the force by the rod on one of the blocks.
View Solution