A person hoists one of two loads of equal mass at a constant velocity v Fig. 15. At the moment when the two loads are at the same height h the upper pulley is released is able to rotate without friction like the lower pulley.Indicate the load which touches the floor first after a certain time t assuming that the person continues to slack the rope at the same constant velocity v. The masses of the pulleys and the ropes and the elongation of the ropes should be neglected.
Immediately after releasing the upper pulley the left load has a velocity v directed upwards while the right pulley remains at rest. The accelerations of the loads will be as if the free end of the rope were fixed instead of moving at a constant velocity. They can be found from the following equations:where m is the mass of each load and T1 and T2 are the tensions of the ropes acting on the left and right loads. Solving the system of equations we obtain a1 = -2/5g and a2 = 1/5g. Thus the acceleration of the left load is directed downwards while that of the right load upwards. The time of fall of the left load can be found from the equationDuring this time the right load will move upwards. Consequently the left load will be the first to touch the floor.
Related Solutions
A person hoists one of two loads of equal mass at a constant velocity v (Fig). At the moment when the two loads are at the same height h, the upper pulley is released (is able to rotate without friction like the lower pulley). Indicate the load which touches the floor first after a certain time t, assuming that the person continues to slack the rope at the same constant velocity v. The masses of the pulleys and the ropes and the elongation of the ropes should be neglected.

View SolutionTwo loads of the same mass are tied to the ends of a weightless inextensible thread passed through a weightless pulley (Fig. ). Initially, the system is at rest,and the loads are at the same level. Then the right load abruptly acquires a horizontal velocity v in the plane of the figure. Which load will be lower in a time?

View SolutionWhen two unequal springs of same material are loaded with same load, which one will have the larger value of time period?
View SolutionA spring having a spring constant K is loaded with mass m. The spring is in two equal parts and one of them is loaded with the same mass. The new spring constant is
View Solutiontwo unequal springs of same material are loaded with same load which one will have large value of time period?
View SolutionTwo unequal springs have same material are loaded with same load. Which one will have a larger value of time period ?
View SolutionA rope of negligible mass can support a load of M kg. What will be the mass of the greatest load raised by the rope? Where g is the acceleration due to gravity and h is the height through which the said load rises from rest with uniform acceleration in time t.
View SolutionWilliam lifts a load by pulling the rope of a pulley system. Which force is applied by William to lift the load?
View SolutionA spring having a spring constant k is loaded with a mass m. The spring is cut into two equal parts and one of these is loaded again with the same mass. The new spring constant i
View SolutionThree loads of mass m_(1),m_(2) and M are suspended on a string passed through two pulleys as shown in Fig. The pulleys are at the same distance from the points of suspension. Find the ratio of masses of the loads at which the system is in equilibrium. Can these conditions always be realized? The friction should be neglected.
View SolutionA person of mass M is at a height h from a floor in a place free from gravitational force. The person throws a ball of mass m, downward with a velocity u. Distance of the person from the floor,when the ball touches the floor, will be
View SolutionA person wishes to slide down a rope whose breaking load is of the weight of the person Minimum acceleration by which the person should slide down without breaking the rope is:
View Solutionएक व्यक्ति ने एक दी हुई सतह पर समान वेग से एक भार (लोड) को चलाने के लिये चित्र में दिखाये गये बल (F) का प्रयोग किया। सही सतह के रेखा-चित्र को पहचानिये:
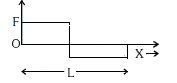
View SolutionA loaded spring vibrates with a period T. The spring is divided into four equal parts and the same load is suspended from one as these parts. The new time period is……………
View SolutionA work of 4900 J is done on a load of mass 50 kg to lift it to a certain height. What is the height through which the load is lifted ?
View SolutionA loaded spring vibrates with a period T. The spring is divided into four equal parts and the same load is divided into four equal parts and the same load is suspended from one end of these parts. The new period is
View Solutionएक रस्सी जड़वत घिरनी के ऊपर से गुजरती है। समान द्रव्यमान के दो लड़के P और Q समान ऊँचाई पर रस्सी के दोनों सिरों पर लटके हैं। दोनों एक साथ समान समय पर ऊपर की तरफ घिरनी तक पहुँचने के लिये चढ़ना आरम्भ करते हैं। P का वेग रस्सी के सापेक्ष v तथा Q का 3v है तो द्वारा घिरनी तक पहुँचने में लगा समय बराबर है।
View SolutionThe armature of a generator of resistance is rotated at its rated speed and produces 125 V without load and 115 V with full load. The current in the armature coil is
View SolutionThe armature of a generator of resistance 1Omega is rotated at its rated speed and produces 125 V without load and 115 V with full load. The current in the armature coil is
View SolutionWhy is it easier to walk with two equal loads in both hands than with the entire load in one hand?
View Solution