An aeroplane flying along the horizontal at a velocity v0 starts to ascend describing a circle in the vertical plane. The velocity of the plane changes with height h above the initial level of motion according to the law v2 = v02 - 2a0h. The velocity of the plane at the upper point of the trajectory is v1 = v0/2.Determine the acceleration a of the plane at the moment when its velocity is directed vertically upwards.
Let us consider the motion of the plane starting from the moment it goes over to the circular path Fig. 130. By hypothesis at the upper point B of the path the velocity of the plane is v1 = v0/2 and hence the radius r of the circle described by the plane can be found from the relationwhich is obtained from the law of motion of the plane for h = 2r. At point C of the path where the velocity of the plane is directed upwards the total acceleration will be the sum of the centripetal acceleration ac = vc2/r vc2 = v02 - 2a0r where vc is the velocity of the plane at point C and the tangential acceleration at this acceleration is responsible for the change in the magnitude of the velocity.In order to find the tangential acceleration let us consider a small displacement of the plane from point C to point C. Then vc2 = v02 - 2a0r + Δh. Therefore vc2 - vc2 = - 2a0Δh where Δh is the change in the altitude of the plane as it goes over to point C. Let us divide both sides of the obtained relation by the time interval Δt during which this change takes place:Then making point C tend to C and At to zero we obtainHence at = -a0. The total acceleration of the plane at the moment when the velocity has the upward direction is then
Related Solutions
An aeroplane flying along the horizontal at a velocity v_(0) starts to ascend, describing a circle in the vertical plane. The velocity of the plane changes with height h above the initial level of motion according to the law v^(2) = v_(0)^(2) - 2a_(0)h . The velcity of the plane at the upper point of the trajectory is v_(1) = v_(0)//2 . Determine the acceleration a of the plane at the moment when its velocity is directed vertically upwards.
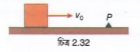
View Solutiona বাহু বিশিষ্ট একটি নিরেট ঘনক একটি মৃসণ অনুভূমিক তলের V0 ওপর বেগ নিয়ে যেতে যেতে P বিন্দুতে একটি পিনের সাথে ধাক্কা খেয়ে উলটে যায়। সেই মুহূর্তে তার কৌণিক বেগ হয়|
View Solutionbody with zero initial velocity moves down an inclined plane from a height hand then ascends along the same plane with an initial velocity such that it stops at the ame height h. In which case is the time of motion longer?
View Solution(A) : If bomb is dropped from an aeroplane moving horizontally with constant velocity then the bomb appears to move along a vertical straight line for the pilot of the plane. ( R) : If a bomb is dropped from an aeroplane moving horizontally with constant velocity then horizontal component of velocity of the bomb remains constant and same as the velocity of the plane during the motion under gravity.
View Solution(A): If a bomb is dropped from an acroplane moving horizontally with constant velocity then the bomb appears to move along a vertical straight line for the pilot of the plane. (R): If a bomb is dropped from an aeroplane moving horizontally with constant velocity then horizontal component of velocity of the bomb remains constant and same as the velocity of the plane during the motion under gravity
View Solutionएक वायुयान क्षैतिज से के कोण पर उड़ रहा है | यदि उसके वेग का ऊर्ध्वाधर घटक 100 मीटर/सेकंड हो तो उसका वास्तविक वेग तथा क्षैतिज घटक ज्ञात कीजिए |
View SolutionAn aeroplane flying at a height of 3000 m passes vertically above another aeroplane at an instant when the angles of elevation of the two planes from some point on the ground are and respectively. Then the vertical distance between the two planes is
View SolutionFor a SHM, the plane difference of velocity and displacement is _____ and the plane difference of velocity and acceleration is _____
View SolutionA solid balanced sphere is stationary on an uneven horizontal plane. A force is applied to the sphere horizontally along its center line. This caused an initial velocity v0 to start sliding on the floor. When it does not slide and start rolling, the center of the sphere will move
View SolutionAn aeroplane takes off at an angle of 60^(@) to the horizontal.If the velocity of the plane is 200kmh^(-1) ,calculate its horizontal and vertical component of its velocity.
View SolutionAn aeroplane takes off at an angle of 60^(@) to the horizontal.If the velocity of the plane is 200kmh^(-1) ,calculate its horizontal and vertical component of its velocity.
View SolutionA body is sliding down an inclined plane of inclination with a uniform velocity. If the body is projected with a velocity u along the plane upwards, show that it will ascend a distance sin along the plane.
View Solutionजब किसी पिण्ड को पृथ्वी तल से h ऊँचाई प्राप्त होने के लिए फेंका जाता है तो उसके प्रक्षेपण वेग का मान निकालिये।
View SolutionA person hears the sound of a jet aeroplane after it has passed over his head. The angle of the jet plane with the horizontal when the sound appears to be coming vertically downwards is . If the velocity of sound is v, then the velocity to the jet plane is :
View Solutionविमान A तथा B नियत वेग से क्षैतिज से क्रमशः कोण बनाते हुए एक ही उर्ध्व तल में उड़ान भर रहे है। जैसा एक चित्र में दर्शाया गया है। विमान A की गति मी/से है । समय t =0 सेकंड पर विमान A में एक प्रेक्षक के अनुसार B उससे 500 मी दुरी पर है। प्रेक्षक के अनुसार विमान B एक नियत वेग से A की गति की लंबवत दिशा में गतिमान है। यदि समय पर विमान A विमान B से टकराने से बाल-बाल बचता है तब समय का सेकंड में मान है।

View SolutionA uniform sphere of radius a rotating with an angular velocity omega about an axis perpendicualr to the plane of motion and its cener impinges on a horizontal plane, let u and v are horizontal and vertical component of velocity before impact. Then
View SolutionA sphere of mass M,, moving with a velocity V0 collides head on with a stationary sphere of mass M. The collision is elastic. V1 and V2 are respectively their velocities immediately after collision.
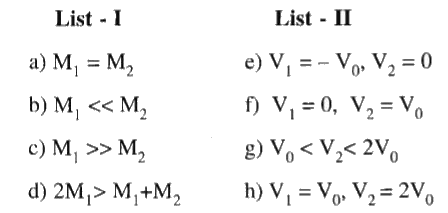
View SolutionA solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
View SolutionA solid cylinder rolls down an inclined plane of height h. What is the velocity of the cylinder when it reaches the bottom of the plane?
View Solutionजमीन पर एक व्यक्ति एक जेट विमान को अपने सर के ठीक ऊपर देखता है जब विमान ऊर्ध्वाधर के साथ का कोण व्यक्ति की आँख पर बनाता है तब ध्वनि सुनाई देती है यदि ध्वनि का वेग v हो, तो जेट विमान का वेग होगा
View Solution