i x2 – 2x – 8 ii 4s2 – 4s + 1 iii 6x2 – 3 – 7x iv 4u2 + 8u v t2 – 15 vi 3x2 – x – 4
i 6x² + 11x + 5 = 06x2 + 11x + 5 = 6x2 + 6x + 5x + 5= 6xx +1 + 5x +1= x +1 6x +5∴ zeroes of polynomial equation 6x2 +11x +5 are { −1 −5/6 }Now Sum of zeroes of this given polynomial equation = −1+ −56 = −11/6But the Sum of zeroes of any quadratic polynomial equation is given by = −coeff.of x / coeff.ofx2 = −11/6And Product of these zeroes will be = −1×−5/6 = 5/6But the Product of zeroes of any quadratic polynomial equation is given by = constant term / coeff.of x2 = 5/6Hence the relationship is verified.ii 4s2 – 4s + 14s2 – 4s + 1 = 4s2 – 2s – 2s + 1= 2s 2s – 1 –12s – 1= 2s – 1 2s – 1∴ zeroes of the given polynomial are: {1/2 1/2}∴ Sum of these zeroes will be = = 1.But The Sum of zeroes of any quadratic polynomial equation is given by = −coeff. of s / coeff.of s2 = −4/4 = 1And the Product of these zeroes will be = 1/2 × 1/2 =1/4But Product of zeroes in any quadratic polynomial equation is given by = constant term/ coeff.of s2 = 1/4.Hence the relationship is verified.iii 6x2 – 3 – 7x6x2 – 7x – 3 = 6x2 – 9x + 2x – 3= 3x 2x – 3 +12x – 3= 3x + 1 2x – 3∴ zeroes of the given polynomial are: – −1/3 3/2∴ sum of these zeroes will be = −1/3 + 3/2 =7/6But The Sum of zeroes in any quadratic polynomial equation is given by = −coeff.of x / coeff.of x2 = 7/6And Product of these zeroes will be = −1/3 × 3/2=−1/2Also the Product of zeroes in any quadratic polynomial equation is given by = constant term / coeff.of x2 = −3/6 = −1/2Hence the relationship is verified.iv 4u2 + 8u4u2 + 8u = 4u u+2Clearly for finding the zeroes of the above quadratic polynomial equation either: – 4u=0 or u+2=0Hence the zeroes of the above polynomial equation will be 0 −2∴ Sum of these zeroes will be = −2But the Sum of the zeroes in any quadratic polynomial equation is given by = −coeff.of u / coeff.of u2 = −8/4 = −2And product of these zeroes will be = 0 × −2 = 0But the product of zeroes in any quadratic polynomial equation is given by = constant term / coeff.of u2 = −0/4 = 0Hence the relationship is verified.v t2 – 15t2 – 15 = t+ √15 t − √15Therefore zeroes of the given polynomial are: – {√15 −√15}∴ sum of these zeroes will be = √15 − √15 = 0But the Sum of zeroes in any quadratic polynomial equation is given by = −coeff.of x / coeff.of x2 = −0/1 = 0 And the product of these zeroes will be = √15 × −√15 = −15But the product of zeroes in any quadratic polynomial equation is given by= constant term / coeff.of t2 = −15/1 = −15Hence the relationship is verified.vi 3x2 – x – 43x2 − x − 4 = 3x2 – 4x + 3x − 4= x 3x – 4 +13x – 4= x + 1 3x – 4∴ zeroes of the given polynomial are: – {−1 4/3 }∴ sum of these zeroes will be = −1 +4/3 = 13But the Sum of zeroes in any quadratic polynomial equation is given by = −coeff.of x / coeff.of x2= −−1/3 = 1/3And the Product of these zeroes will be = {−1 × 4/3 }= −4/3But the Product of zeroes in any quadratic polynomial equation is given by = constant term / coeff.of x2 = −4/3Hence the relationship is verified.
Related Solutions
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. -
(i)
(ii)
(iii)
(iv)
(v)
(vi)
View SolutionFind the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. - (i) (ii) (iii) (iv) (v) (vi)
View Solutionनिम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सबंध की सत्यता की जाँच कीजिए :
View SolutionIf it is 4 = then then it's on if1 x = 6x2-1 male -(11) x2 = 3 + 2.12(III) x2 = 3 - 22(IV) xi = 6x2 + 1(2) 1.1V(3) I, III(4) I, II, III, IV
View Solutionनिम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए :
(i)
(ii)
(iii)
.(iv)
(iv)
View SolutionIdentify:
i.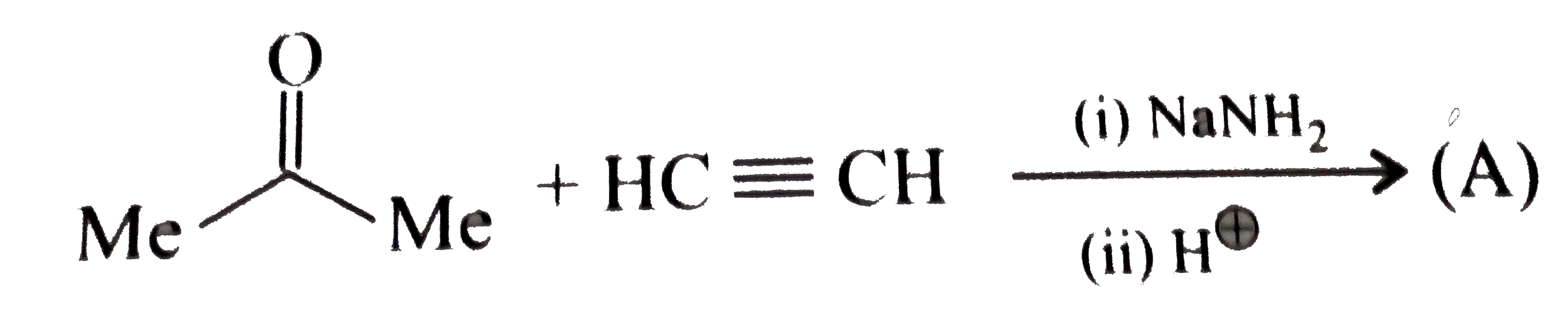
ii.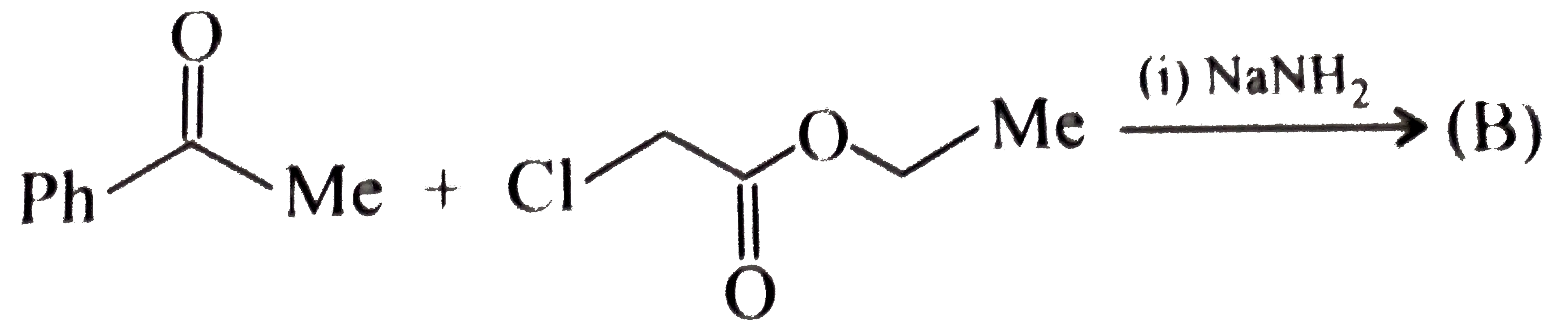
iii.
iv.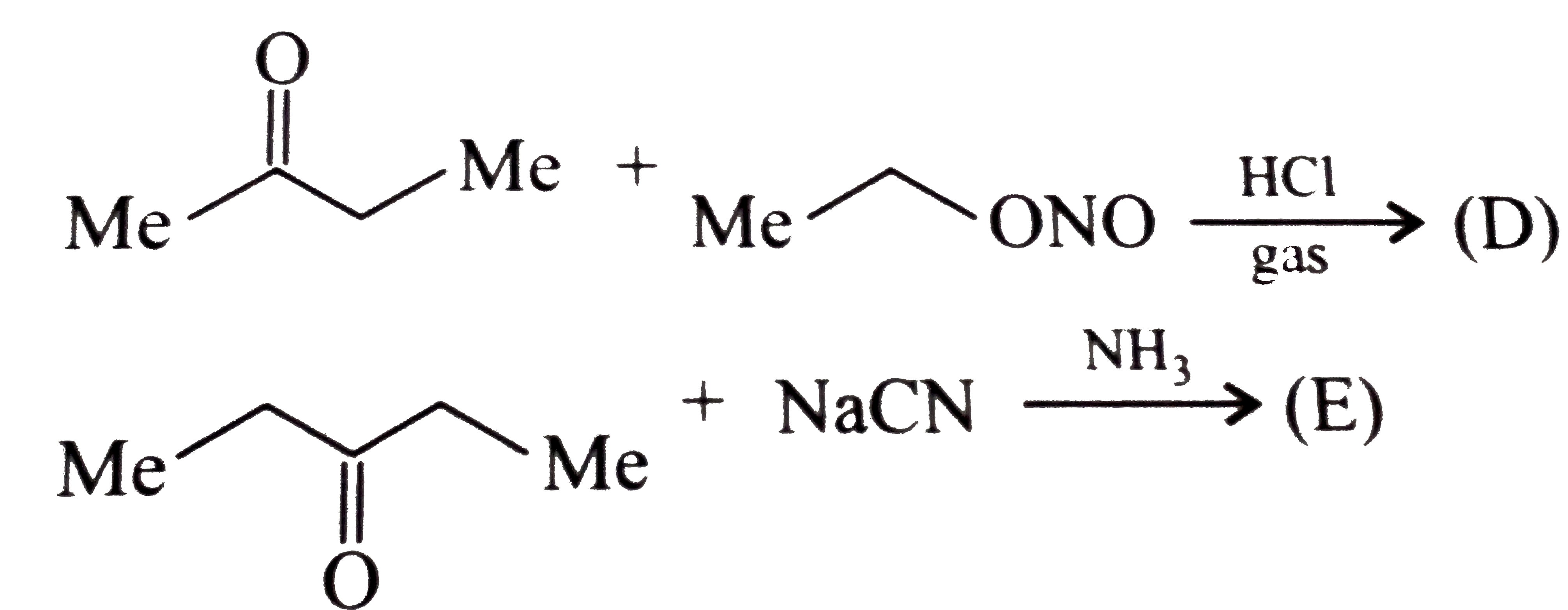
v.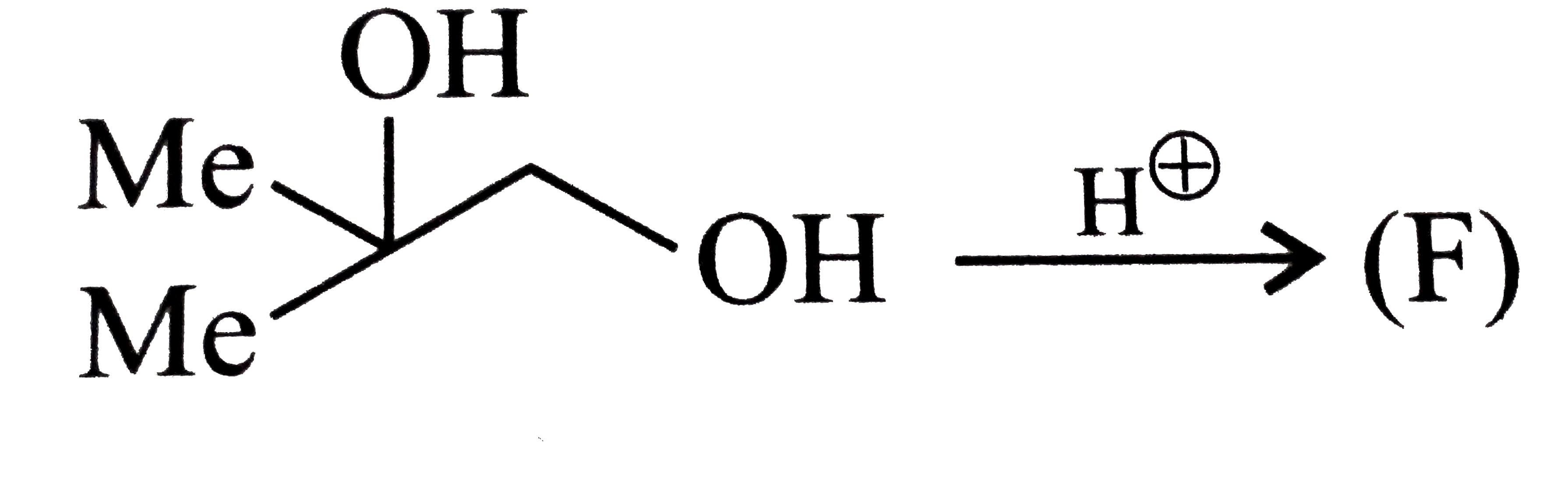
vi.
View Solutionनिम्न बहुपदो के शून्यको तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए :
(ii)
View Solutionरिक्त स्थानों को भरें ताकि कथन सत्य हो :
View SolutionFind four rational number equivalent to each of the following.
(i)
(ii)
(iii)
(iv) 8
(v) 1
(vi) -1
View SolutionExpand using binomial theorem:
View SolutionAdd the following rational numbers:
View SolutionIf find the values of
(i)
(ii)
(iii)
(iv)
(v)
(vi)
View SolutionEvalute
(i) (ii) (iii)
(iv) (v) (vi)
View SolutionTest the divisibility of :
(i) 10000001 by 11, (ii) 19083625 by 11, (iii) 2134563 by 9 , (iv) 10001001 by 3 , (v) 10203574 by 4 , (vi) 12030624 by 8
View SolutionDetermine the degree of each of the following polynomials.
(i)
(ii)
(iii)
(iv)
(v)
(vi)
View SolutionDivide:
(i) 12 by 8
(ii) 63 by 15
(iii) 47 by 20
(iv) 101 by 25
(v) 31 by 40
(vi) 11 by 16
View SolutionEvaluate
I 15+(-8)
ii (-16)+9
iii (-7)+(-23)
iv (-32)+47
v 53+(-26)
vi (-48)+(-36)
View SolutionFind the value of
View SolutionFind the values of :-
(i)
(ii)
(iii)
(iv)
(v)
(vi)
View SolutionFind the values of :-
(i)
(ii)
(iii)
(iv)
(v)
(vi)
View Solution