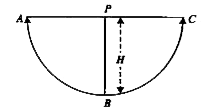
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H.If the acceleration due to gravity is g then the velocity of the bob as it passes through B isa mgHb √2gHc zerod 2gH.
Correct option b √2gHExplanation:Potential energy at A or C = Kinetic energy
Related Solutions
A simple pendulum with a bob of mass m oscillates from A to C and back to such that PB is H. If the acceleration due to gravity is g, then the velocity of the bob as it passes through B is………..

View SolutionA simple pendulum with a bob of mass 'm' oscillates from A to C and back to A such that PB is H. If the acceleration due to gravity is 'g' , then the velocity of the bob, as it passes through B, is

View SolutionA simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. If the acceleration due to gravity is g, then the velocity of the bob as it passes through B is
View SolutionA simple pendulum with a bob of mass m oscillates from A to C and back to A, such that PB=h, If the acceleration due to gravity is 'g', then the velocity of the bob as it passes through B is
View SolutionA simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
View SolutionA simple pendulum with a bob of mass ‘m’ oscillates from A to C and back to A such that PB is H . If the acceleration due to gravity is ‘g’ then the velcoity of the bob as it passes through B is
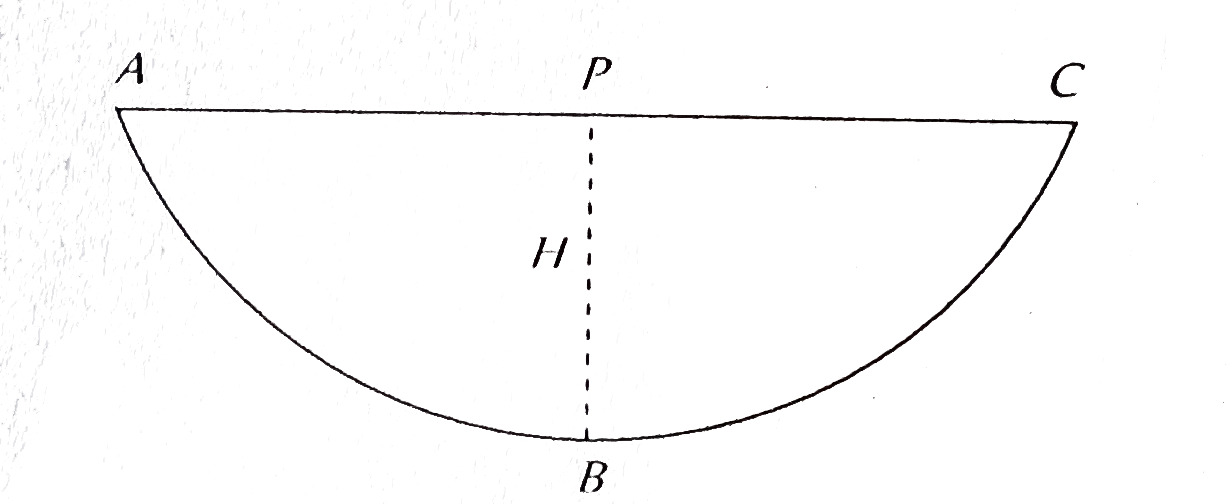
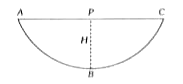
View Solutionm ' द्रव्यमान के गोलक वाला एक सरल लोलक A से C तक दोलन करता है और फिर A पर वापस लोट आता है। PB की दुरी 'H ' है गुरुत्व के कारण त्वरण 'g ' है जब गोलक B से गुजरता है ,तब उसका वेग होगा।
View SolutionA ball of mass 'm' moving with a horizontal velocity 'v' strikes the bob of mass 'm' of a pendulum at rest. During this collision, the ball sticks with the bob of the pendulum. The height to which the combined mass raises is (g = acceleration due to gravity).
View SolutionA ball of mass 'm' moving with a horizontal velocity 'v' strikes the bob of mass 'm' of a pendulum at rest. During this collision, the ball sticks with the bob of the pendulum. The height to which the combined mass raises is (g = acceleration due to gravity).
View SolutionConsider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its time period using method of dimensions.
View SolutionConsider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its time period using method of dimensions.
View SolutionConsider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its time period using method of dimensions.
View SolutionConsider a simple pendulum having a bob attached to a string that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l) , mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its time period using the method of dimensions.
View SolutionConsider a simple pendulum, having a bob attached to a string , that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple. Pendulum depends on its length ( l) , mass of the bob ( m ) , and acceleration due to gravity ( g ) . Derive the expression for is time period using method of dimension .
View SolutionConsider a simple pendulum having a bob attached to a string that oscillates under the action of a force of gracity. Suppose that the period of oscillation of the simple pendulum depends on its length (I), mass of the bob (m) and acc. Due to gravity (g). Derive the expression for its time period using method of dimensions.
View Solutionm દળ ધરાવતા ગોળાનું બનેલું સાદું લોલક A થી Cસુધી દોલન કરી ફરી પાછું A પાસ એવી રીતે આવે છે કે જેથી PB = H થાય. જો ગુરૃત્વાકર્ષણને લીધે ઉદૂભવતો પ્રવેગ g હોય, તો ગોળો B બિંદુ પાસેથી પસાર 'થાય ત્યારે તેનો વેગ

View SolutionThe time period Of oscillation of a simple pendulum depends on the following quantities
Length of the pendulum (l),
Mass of the bob (m), and
Acceleration due to gravity (g)
Derive an expression for Using dimensional method.
View SolutionThe period of oscillation (T) of a simple pendulum depends on the probable quantities such as mass 'm' of a bob, length 'l' of the pendulum and acceleration due to gravity 'g' at the place. Derive an equation using dimensional analysis.
View SolutionThe time period Of oscillation of a simple pendulum depends on the following quantities
Length of the pendulum (l),
Mass of the bob (m), and
Acceleration due to gravity (g)
Derive an expression for Using dimensional method.
View SolutionDerive dhe formula for the period of oscillation of a simple pendulum using dimensions. The period of oscillation of a simple pendulum depends on (a) the mass of the bob m (b) the length of the pendulum (c) acceleration due to gravity g (d) angular displacement theta
View Solution