Prove that Diagonals of a parallelogram divides it into two triangles of equal area.
Given:ABCD is a parallelogram. AC is one of the diagonals of the parallelogram ABCD.To prove:arΔABC=arΔDBCProof:In triangles ABD and DBC AB = DC Opposite sides of parallelogramAD = BC Opposite sides of parallelogramBD = BD common sidearea congruency axiom
Related Solutions
Prove that two diagonals of a parallelogram divides it into four triangles of equal areas.
View SolutionProve that A diagonal of a parallelogram divides it into two triangles of equal area.
View Solutionसिद्ध कीजिए कि समान्तर चतुर्भुज के विकर्ण उस समान्तर चतुर्भुज को बराबर क्षेत्रफल के चार त्रिभुजों में बाँटते है।
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area.
View Solutionसमान्तर चतुर्भुज के विकर्ण उसे दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करते है।
View Solutionयदि किसी चतुर्भुज का प्रत्येक विकर्ण इसे बराबर क्षेत्रफल वाले दो त्रिभुजों में बाटता हो तो सिद्ध कीजिए की वह चतुर्भुज एक समांतर चतुर्भुज होता है।
यदि किसी चतुर्भुज के विकर्ण चतुर्भुज को बराबर क्षेत्रफल वाले चार त्रिभुजों में बाटे तो सिद्ध करे की वह एक समांतर चतुर्भुज होगा।
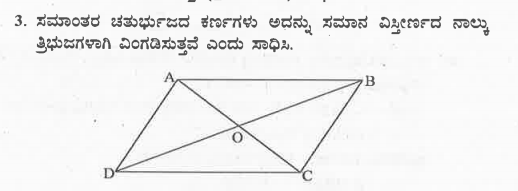
View Solutionಸಮಾಂತರ ಚತುರ್ಭುಜದ ಕರ್ಣಗಳು ಅದನ್ನು ಸಮಾನ ವಿಸ್ತೀರ್ಣದ ನಾಲ್ಕು ತ್ರಿಭುಜಗಳಾಗಿ ವಿಂಗಡಿಸುತ್ತವೆ ಎಂದು ಸಾಧಿಸಿ.
View Solutionसिद्ध करें कि समांतर चतुर्भुज के विकर्ण इसे बराबर क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते हैं।
View SolutionA diagonal of parallelogram divides it into four triangles of equal area.
View SolutionA diagonal of parallelogram divides it into four triangles of equal area.
View Solutionਦਰਸਾਉ ਕਿ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਦੋਨੋਂ ਵਿਕਰਣ ਉਸਨੂੰ ਬਰਾਬਰ ਖੇਤਰਫਲਾਂ ਵਾਲੇ ਚਾਰ ਤ੍ਰਿਭੁਜਾਂ ਵਿੱਚ ਵੰਡਦੇ ਹਨ।
View SolutionProve that if each diagonal of a quadrilateral bisects it into two triangles of equal areas, then it is a parallelogram.
View SolutionEach diagonal of a parallelogram is equal to "............. " Divides into two triangles.
View Solutionयदि किसी चतुर्भुज का प्रत्येक विकर्ण इसे दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करे, तो सिद्ध कीजिए कि यह चतुर्भुज समान्तर चतुर्भुज है।
View Solution'If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
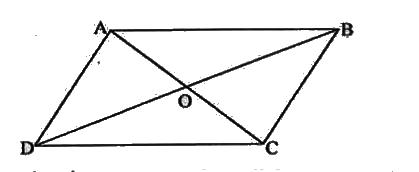
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View Solution