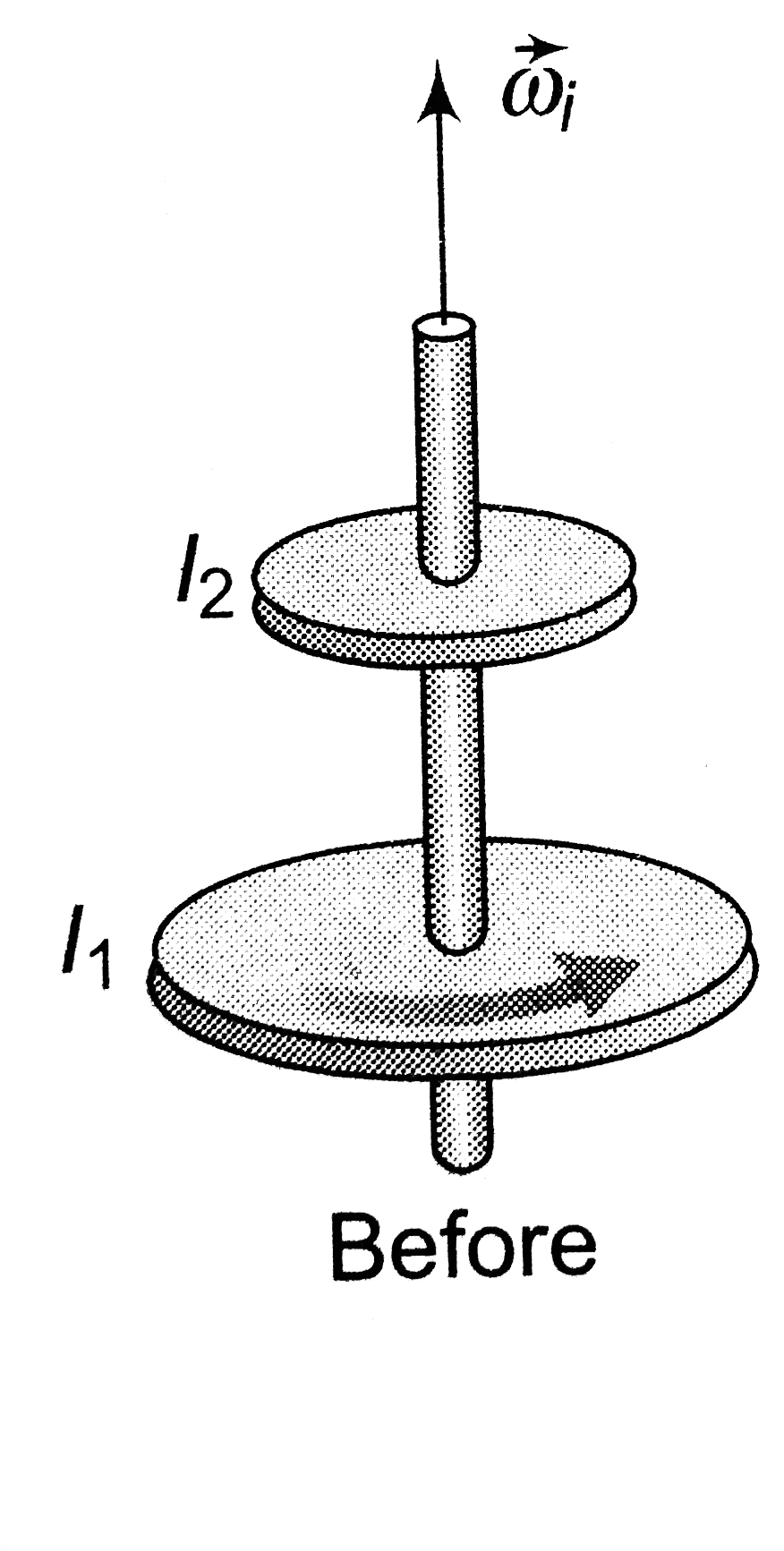
A circular disk of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular speed ωi. Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk. Initially the second disk has zero angular speed. Eventually both the disks rotate with a constant angular speed ωf The energy lost by the initially rotating disc to friction is
Correct option dExplanation:As no external torque is applied to the system the angular momentum of the system remains conserved.:. Li = LfAccording to given problem
Related Solutions
A circular disk of moment of inertia is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed . Another disk of moment of inertia is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed . The energy lost by the initially rotating disc to friction is
View SolutionA circular disk of moment of inertia I_t is rotating in a horizontal plane, about its symmetry axis,with a constant angular, speed omega_1 Another disk of moment of inertia I_b is dropped coaxially onto the rotating disk initially the second disk has zero angular speed.Eventually both the disks rotate with a constant angular speed omega_f The energy lost by the initially rotating disc to friction is :
View Solutionजड़त्व आघूर्ण की एक वृत्ताकार डिस्क अपनी सममिति अक्ष के परितः, एक स्थिर कोणीय वेग से क्षैतिज तल में घूर्णन कर रही है। इस डिस्क के ऊपर जड़त्व आघूर्ण की एक अन्य डिस्क संकेन्द्री डाल दी जाती है। प्रारंभ में दूसरी डिस्क की कोणीय चाल शून्य है। अन्ततः दोनों डिस्क एक ही स्थिर कोणीय वेग से घूर्णन करने लगती हैं। प्रारंभ में घूर्णन करती हुई डिस्क की घर्षण के कारण नष्ट हुई ऊर्जा है ।
View SolutionA disk with moment of inertia rotates about frictionless, vertical axle with angular speed A second disk, this one having moment of inertia and initial not rotating, drops onto the first disk (Fig.) Because of friction between the surfaces, the two eventually reach the same angular speed . The value of is.
 .
.
View Solutionநிலைமத் திருப்புத் திறன் கொண்ட வட்டத்தட்டு மாறாத கோண திசைவேகம் வுடன் கிடைத்தளத்தில் சமச்சீரான அச்சைப் பற்றி சுழல்கிறது. ஓய்வு நிலையிலுள்ள மற்றொரு வட்டத்தட்டின் என்ற நிலைமத்திருப்புத்திறனுடன் சுழலும் வட்டத்தட்டின் மீது அச்சுழலும் அச்சிலேயே விடப்படுகிறது. இதனால் இரு வட்டத்தட்டுகளும் மாறா கோண வேகத்தில் சுழல்கிறது. இந்நிகழ்வில் உராய்வினால் ஏற்படும் ஆற்றல் இழப்பு
View SolutionA disc of moment of inertia la is rotating in a horizontal plane about its symmetry axis with constant angular speed co. Another discinitially at rest of moment of inertia I, is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed The loss of kinetic energy due to friction in this process is,
View SolutionA circular disc of moment of inertia is rotating in a horizontal plane, about its symmetry axis, with a constant angular speed . Another disc of moment of inertia is placed coaxially on the rotating disc. Initially the second disc has zero angular speed. Eventually both the discs rotate with a constant angular speed . The energy lost by the initially rotating disc to friction is ............
View SolutionA circular disc of moment of inertia is rotating in a horizontal plane about its symmetry axis with a constant angular velocity . Another disc of moment of inertia is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed . Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA circular disc of moment of inertia I_(t) is rotating in a horizontal plane about its symmetry axis with a constant angular velocity omega_(i) . Another disc of moment of inertia I_(b) is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed omega_(f) . Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA disc of moment of inertia la is rotating in a horizontal plane about its symmetry axis with constant angular speed co. Another discinitially at rest of moment of inertia I, is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed The loss of kinetic energy due to friction in this process is,
View SolutionA disc of moment of inertia I_(a) is rotating in a horizontal plane about its symmetry axis with a constant angular speed ω. Another discinitially at rest of moment of inertia I_(b) is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed. The loss of kinetic energy due to friction in this process is,
View SolutionTwo disks are rotating about the same axis. Disk A has a moment of inertia of and an angular velocity of . Disk B is rotating with an angular velocity of . The two disks are then linked together without the aid of any external torques, so that they rotate as a single unit with an angular velocity of . The axis of rotation for this unit is the same as that for the separate disks. What is the moment of inertia of disk B?
View SolutionA thin circular disk of radius R is uniformly charged with density per unit area. The disk rotates about its axis with a uniform angular speed . The magnetic moment of the disk Is
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA disc of moment of inertia , is rotating in horizontal plane about an axis passing through its centre and perpendicular to its plane with constant angular speed . Another disc of moment of inertia having angular speed The energy lost by the initial rotating disc is
View SolutionDisk 1 rotates about a smooth vertical axis with the angular velocity omega_(1) . Disk 2 rotating with the angular velocity omega_(2) is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to I_(1)andI_(2) , respectively. The constant surface of the disks are rough.
View SolutionA circular disk of radius 0.010 m rotates with a constant angular speed of 5.0 rev/s. What is the acceleration of a point on the edge of the disk?
View SolutionA disc of the moment of inertia 'l_(1)' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'omega_(1)' . Another disc of moment of inertia 'I_(2)' . having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed 'omega_(2)' . The energy lost by the initial rotating disc is
View SolutionA disc of the moment of inertia 'l_(1)' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'omega_(1)' . Another disc of moment of inertia 'I_(2)' . having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed 'omega_(2)' . The energy lost by the initial rotating disc is
View Solution