In youngs double slit experiment distance between the slits is d and that between the slits and screen is D. Angle between principle axis of lens and perpendicular bisector of S1 and S2 is 45°. The point source S is placed at the focus of lens and aperture of lens is much larger than d. Assuming only the reflected light from plane mirror M is incident on slits distance of Central Maxima from O will be:
Related Solutions
In youngs double slit experiment, distance between the slits is d and that between the slits and screen is D. Angle between principal axis of lens and perpendicular disector of and is . The point source S is placed at the focus of lens and aperture of lens is much larger then d. Assuming only the reflected light from plane mirror M is incident on slits, distance of central maxima from O will be :

View SolutionIn youngs double slit experiment, distance between the slits is d and that between the slits and screen is D. Angle between principal axis of lens and perpendicular disector of and is . The point source S is placed at the focus of lens and aperture of lens is much larger then d. Assuming only the reflected light from plane mirror M is incident on slits, distance of central maxima from O will be :

View SolutionIn a young’s double slit experiment the distance between slits S1 and S2 is d and distance of slit plane from the screen is . The point source of light (S) is placed a distance below the principal axis in the focal plane of the convex lens (L). The slits S1 and S2 are located symmetrically with respect to the principal axis of the lens. Focal length of the lens is .
Find the distance of the central maxima of the fringe pattern from the centre (O) of the screen.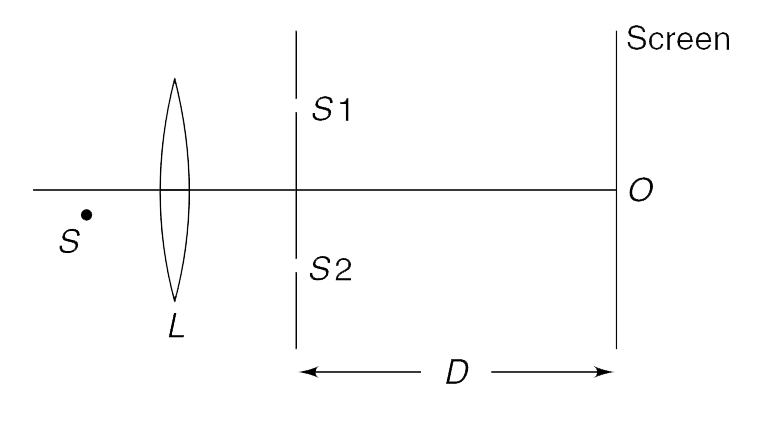
View SolutionIn Young's double-slit experiment, the slits S_1 And S_2 The distance between the slits is d and the distance between the slits and the screen is D. then the longest wavelength which S_1 will be absent on the screen in front of:
View SolutionIn Young's double slit experiment, if the gap between the slits is halved, then for the fixed wavelength and the distance between the screen and the slits-
View Solutionयंग के द्वि-स्लिट प्रयोग में रेखाछिद्रों को श्वेत प्रकाश से प्रकाशित किया गया है | दोनों रेखाछिद्रों के मध्य दूरी b है तथा उनसे पर्दा d दूरी पर है | पर्दे पर रेखाछिद्र के ठीक सामने कुछ तरंगदैर्घ्य अनुपस्थित हैं, वे हैं
View SolutionIn Young's double-slit experiment, the slits are illuminated with white light. The distance between the two slits is b and the screen is at a distance d from them. There is absence of some wavelength just in front of the slit on the screen, they are
View SolutionIn Young's double experiment , in air interference pattern second minimum is observed exactly in front of one slit. The distance between the two coherent source is 'd' and the distance between source and screen 'D'. The wavelength of light source used is
View SolutionIn Young's double slit experiment, if the distance between the slits is halved and the distance between the slits is halved, then the width of the fringe
View SolutionIn Young's double-slit experiment, white light is used to illuminate two slits. The separation between the slits is d and the distance between the slits and the screen is D(d lt lt D) Is. At a point on the screen directly in front of one of the two slits, some wavelengths are absent. missing wavelengths are
View SolutionIn a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
View SolutionIn a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
View SolutionIn Young 's double slit experiment the distance between the slits and the screen is doubled the separation between the slits is reduced to half. As a result the fringe width.
View SolutionIn Young's double-slit experiment, if the gap between the slits is halved, and the distance between the slits and the screen is doubled, then the width of the fringe compared to the original value
View SolutionIn Young's double slit experiment, the slits are at a distance d and the interference pattern is obtained on a screen at a distance d from the slits. A dark fringe is observed opposite one of the slits, then the wavelength of light will be
View SolutionIn a Young's double slit experiment, the separation between the slits is d, distance between the slit and screen is . In the interference pattern, there is a maximum exactly in front for each slit. Then the possible wavelength (s) used in the experiment are
View SolutionIn Young's double-slit experiment, the distance between the slits is 1 mm and the screen is located at 1 m from the slits. For monochromatic light of wavelength 500 nanometers, the distance of the third minimum from the central maximum will be
View SolutionIn the Youngs double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled, the fringe width will be :
View SolutionIn Young's double slit experiment, the distance between two slits is 0.1 mm. If the screen is placed at a distance of 1.0 m from the slits and the wavelength of light 5000 Å , then the fringe width is:
View Solutionयंग के प्रयोग में यदि दोनों स्लिटों के बीच की दूरी आधा तथा स्लिट और पर्दे के बीच की दूरी दुगुनी कर दी जाती हैं तो फ्रिंज - चौड़ाई हो जायेगी -
View Solution