WORK, ENERGY AND POWER for Class 9 PHYSICS
INTRODUCTION
Hamari life me work aur energy bahut important role play karte hain.
Phle hum work ke concept ko samjhte hain. Work kab hota hai? Jab hum homework krte hain ya phir koi assignment complete krte hain ya jab hum pure force se wall ko push krte hain? Kya ye physics ke according work hai? No. So, Work done kab hoga according to physics? Work tab hota hai jab force aur displacement hota hai, jab hum kisi object pr force apply krte hain aur uska displacement hota hai.
Energy modern civilization ka bahut hi important building block hai. Koi bhi body jo work krne me capable ho wo energy possess karta hai. Energy ke bahut sare forms hote hain aur energy almost hr phenomena me involve hoti hai aur ye physics ka ek bahut important concept hai. Total amount of energy jo hai pure universe me wo constant hota hai.
WORK
Work done hota hai jab force aur displacement (movement of the object)
hota hai. Jab object pr koi force or koi displacement nahi hota hai to koi work done nahi hota hai. Work done tab hota hai jab hum kisi object pr force lagate hain aur vo object move krta hai. Example: Coolie work krta hai load utha kr apne sir pr aur vo force of gravity ke against me hota hai. Force exerted by the coolie aur displacement dono hi upward direction me hain. Displacement of object yaha zero hai so work done bhi zero hoga.
Work is defined as a force acting upon an object to cause a displacement. It is expressed as the product of force and displacement in the direction of force.
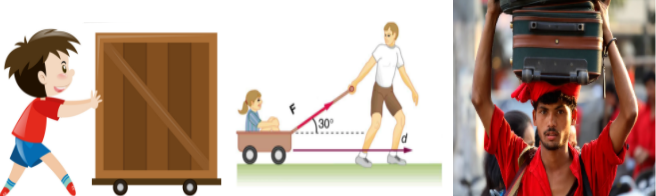
Uper ke pictures se hum ye follow krte hain ki work done tab hota hai jab :
(1) Kisi object pr hum force apply krte hai.
(2) Aur vo object apne original position se displace hota hai.
These two conditions need to be satisfied for work to be done.
Examples :
Jab hum ground pr rakhe pebble ko move krte hain ek distance pr to hum pebble pr force exert karte hain aur pebble displace hota hai. Yaha work done hua.
Jab hum ek force lift krte hain kisi height pr to hum uspr force exert karte hain. Book pr force apply hua hai aur book displace kiya hai. So yaha work done hua.
WORK DONE BY A CONSTANT FORCE
Object ke displacement ka direction aur force ka direction dono ka alag alag relation ho sakta hai. Force aur displacement ka direction ho sakta hai ki :(1) same ho
(2) opposite ho
(3) perpendicular to each other ho
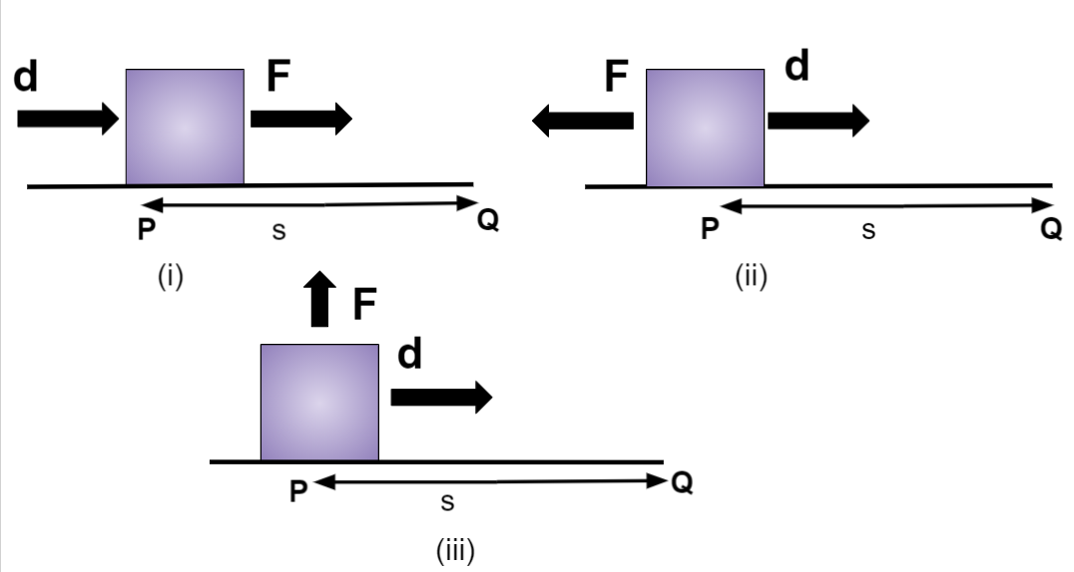
Work done negative, positive or zero ho sakta hai. Niche diye image me aap dekhenge
(i) Work done positive hai kyunki force aur displacement dono same direction me act kr raha hai.
(ii) Work done negative hai kyunki force aur displacement dono opposite direction me act kr raha hai.
(iii) Work done zero hai kyunki force aur displacement dono ek dushre ke perpendicular hai.
Positive work by a force body ke speed ko increase karta hai. Negative work by a force body ke speed ko decrease karta hai. Zero work by a force body ke speed pr koi effect nahi karta hai.
W=F×d
Yaha pr W work done hai, F force hai aur d displacement hai.
Unit :- Work ka S.I. unit joule (J) hai.
Work scalar quantity hai. Work ka koi magnitude aur direction nahi hota hai.
OMR (One Minute Revision)
- * The amount of work done by a force is equal to the product of force and displacement.
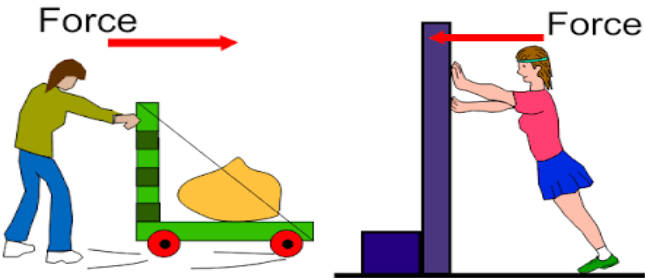
* If a force acts on a body and the body does not move (displacement is zero), then no work is done. For example, pushing a wall.
* The coolie does work against the force of friction when he moves with the load.
* Conditions for work done by a force to be zero:
- (a) When there is no displacement (S= 0).
(b) When displacement is normal to the direction of force (θ= 90°).
* W=FS=mgh
* Work done does not depend on time.
POINT 1
Work : It is defined as a force acting upon an object to cause a displacement. It is expressed as the product of force and displacement in the direction of force.
EXAMPLE 1
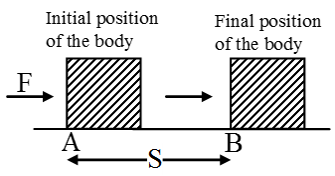
A force of 5 N is acting on an object. The object is displaced through 2 m in the direction of the force (Fig.).
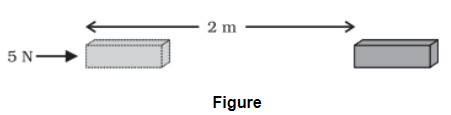
If the force acts on the object all through the displacement,
then work done is 5N×2m=10Nm
or 10J.
EXAMPLE 2
A porter lifts a luggage of 15 kg from the ground and puts it on his head 1.5 m above the ground. Calculate the work done by him on the luggage.
Mass of luggage, m=15kg
and displacement, h=1.5m.
g=10m/s2
As work done by an object is equal to the potential energy stored in an object.
Therefore,
W=mgh
=15×10×1.5
=225J.
EXAMPLE 3
A force of 7 N acts on an object. The displacement is, say 8 m, in the direction of the force (see Figure below). Let us take it that the force acts on the object through the displacement. What is the work done in this case ?

We know that : Work done=Force × Displacement
Or W=F×s
Here Force, F=7N
And Displacement, s=8m
So, W=7×8J
or W=56J
Thus, the work done in this case is 56 joules.
EXAMPLE 4
The velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of the motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
Consider an object of mass m moving with uniform velocity u.
Let, it now be displaced through a distance s, when a constant force F acts on it in the direction of its displacement.
From the third equation of motion,
v2=u2+2as
⇒v2−u2=2as
⇒s=v2−u22a .....(i)
We know that, work done by F is
W=Fscosθ (since, force and displacement are in same direction so (θ=0∘)
=ma.s [∵F=ma]
=maxx((v^(2)-u^(2))/(2a))[omEq.(i)]
W=12m(v2−u2) ....(ii)
If the object is starting from its stationary position i.e., u=0, from Eq. (ii), we get
W=12mv2
If is clear that the work done is equal to the change in the kinetic energy of an object.
ENERGY
Energy ke bina life impossible hai. Sun sabse badha source of energy hai. Koi bhi body jo work krne me capable ho wo energy possess krta hai. Kisi body ki jo kaam krne ki chhamta hoti hai usse energy kahte hai. Jab koi body work karta hai to uska energy decrease ho jata hai aur jab koi body pr work hota hai to uska energy increase ho jata hai. Iska matlab jab bhi koi work hota hai vaha hamesha transfer of energy hota hai.
Energy scalar quantity hai.
The energy of a body may be defined as the capacity of a body to do work.
UNITS OF ENERGY
Work or energy ka same units hota hai.
Energy ka S.I unit joule (J) or C.G.S unit erg hai.
'1 J = 10^7 erg'
Energy ka bigger units watt hour (Wh) aur kilowatt hour (kWh) hai.
DIFFERENT FORMS OF ENERGY
Energy bahut sare forms me ho sakta hai. Sound energy, Mechanical energy (Potential energy + Kinetic Energy), Chemical energy, Heat energy, Electrical energy, Nuclear energy, Light energy, energy ke different forms hai. Energy ek form se dusre form me change hote hainMechanical Energy : Mechanical energy potential energy aur kinetic energy ka sum hota hai. Kisi object ko uski shape, size, configuration, position ya motion ke liye jo energy requirement hoti hai usse mechanical energy kahte hai.
The energy possessed by a body due to its state of rest or of motion, is called mechanical energy. Mechanical energy is the total amount of kinetic energy and potential energy of an object that is used to do a specific work.
ME=KE+PE
PE=mgh
KE=12mv2
Examples of Mechanical Energy: Aeroplane, rain drops, waterfall, flying birds. Kyuki yaha height aur velocity dono hai.
POTENTIAL AND KINETIC ENERGY
Potential Energy
The energy possessed by a body at rest due to its position or size and shape is called potential energy.Kisi object ko uski shape, size, configuration ya position ke liye jo energy requirement hoti hai usse potential energy kahte hai. Jab hum kisi object ko raise karte hain ek height pr to uska energy increase ho jata hai kyuki work done gravity ke against hota hai. Jo energy in object me present hota hai usko gravitational potential energy kahte hain. Potential energy is the energy due to height.
The gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity.
Examples of Potential Energy: Koi body jo above the ground hai aur ek height pr placed hai, koi stretched rubber string, koi compressed spring, bent bow.

Kinetic Energy (K)
Kisi object ko uski motion ke liye jo energy requirement hoti hai usse kinetic energy kahte hai.
The energy possessed by a body because of its motion is called its kinetic energy.
All moving bodies have kinetic energy.
Expression for Kinetic Energy :
Ager kisi object ka mass m hai, uniform velocity u hai, displacement s hai, constant force F hai to Work done F×s hoga. Work done object pr uska velocity change kar dega aur velocity v se u hoga aur a acceleration hoga.
v2–u2=2as
s=v2–u22a
'W = m a xx v^2– u^2/ 2a'
W = ½ m (v^2 – u^2)
W=½mv2
Ager u=0 hai, to work done ½mv2 ho jaega.
'KE= ½ mv^2'
DIFFERENCE BETWEEN POTENTIAL ENERGY AND KINETIC ENERGY
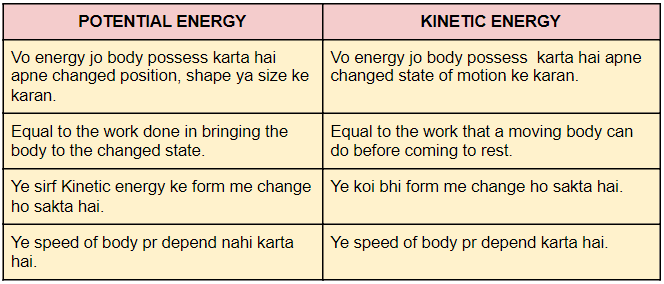
ENERGY CONVERSION
Energy ke form me change hota rehta hai.
Waterfall ke top me Potential energy hai, kyuki height involve hai aur water ka mass hai. Jab water fall hota hai to height decrease hota hai aur potential energy bhi decrease hota hai. Jab water fall ho raha velocity ke saath to energy convert ho raha potential energy se flowing water ke kinetic energy me.
Example of Energy Conversion in a ball : Jab kisi ball ko ek height se fall krte hai towards the ground, to potential energy kinetic energy me change hota hai.
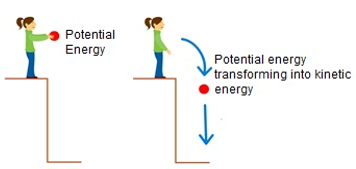
LAW OF CONSERVATION OF ENERGY
Energy na create hota hai na destroy hota hai vo ek form se dushre form me transform hota hai. Total energy jo hota hai vo tanformation ke pehle or baad me same hota hai.
Whenever energy gets transformed,the total energy remains unchanged. According to this law, energy can only be converted from one form to another, it can neither be created or destroyed. The total energy before and after transformation remains the same. As the ball falls, its potential energy will change into kinetic energy.
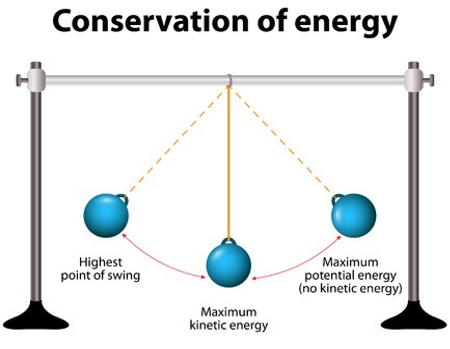
Total energy = KE + PE
Jab potential energy aur kinetic energy ke beech interchange hota hai tab total mechanical energy constant rehta hai.
K+U=constant
DIFFERENCE BETWEEN POTENTIAL ENERGY AND KINETIC ENERGY

ENERGY CONVERSION
Energy ke form me change hota rehta hai.Waterfall ke top me Potential energy hai, kyuki height involve hai aur water ka mass hai. Jab water fall hota hai to height decrease hota hai aur potential energy bhi decrease hota hai. Jab water fall ho raha velocity ke saath to energy convert ho raha potential energy se flowing water ke kinetic energy me.
Example of Energy Conversion in a ball : Jab kisi ball ko ek height se fall krte hai towards the ground, to potential energy kinetic energy me change hota hai.

LAW OF CONSERVATION OF ENERGY
Energy na create hota hai na destroy hota hai vo ek form se dushre form me transform hota hai. Total energy jo hota hai vo tanformation ke pehle or baad me same hota hai.Whenever energy gets transformed,the total energy remains unchanged. According to this law, energy can only be converted from one form to another, it can neither be created or destroyed. The total energy before and after transformation remains the same. As the ball falls, its potential energy will change into kinetic energy.

Total energy = KE + PE Jab potential energy aur kinetic energy ke beech interchange hota hai tab total mechanical energy constant rehta hai. K+U=constant
OMR (One Minute Revision)
- * A body capable of doing work is said to possess energy.
* Work and energy are related to each other.
* Energy spent does not depend on time.
* There is no transfer of energy if a body is acted upon by a force normal to the direction of its displacement.
* Total mechanical energy is the sum of its potential energy and kinetic energy. Total mechanical energy is the sum of its potential energy and kinetic energy.
* Gravitational potential energy =mgh
POINT 2
Energy :
The energy of a body may be defined as the capacity of a body to do work.
Mechanical Energy :
The energy possessed by a body due to its state of rest or of motion, is called mechanical energy.
Mechanical energy is the total amount of kinetic energy and potential energy of an object that is used to do a specific work.
Potential Energy : :
The energy possessed by a body at rest due to its position or size and shape is called potential energy.
Kinectic Energy :
The energy possessed by a body because of its motion is called its kinetic energy. All moving bodies have kinetic energy.
EXAMPLE 5
An object of mass 15 kg is moving with a uniform velocity of 4ms–1. What is the kinetic energy possessed by the object?
Mass of the object, m=15kg, velocity of the object, v=4ms–1.
From Eq. ,
Ek=12mv2
=12×15kg×4ms–1×4ms–1
=120J
The kinetic energy of the object is 120 J.
EXAMPLE 6
What is the work to be done to increase the velocity of a car from 30kmh–1 to 60kmh–1 if the mass of the car is 1500 kg?
Mass of the car, m=1500kg,
initial velocity of car, u=30kmh–1
=30×1000m60×60s
=8.33ms–1.
Similarly, the final velocity of the car,
v=60kmh–1
=16.67ms–1.
Therefore, the initial kinetic energy of the car,
Eki=12mu2
=12×1500kg×(8.33ms–1)2
=52041.68J.
The final kinetic energy of the car,
Ekf=12×1500kg×(16.67ms–1)2
=208416.68J.
Thus, the work done = Change in kinetic energy
=Ekf–Eki=156375J
EXAMPLE 7
Find the energy possessed by an object of mass 10 kg when it is at a height of 6 m above the ground. Given, g=9.8ms–2.
Mass of the object, m=10kg,
displacement (height), h=6m, and
acceleration due to gravity, g=9.8ms–2.
From Eq.,
Potential energy =mgh
=10kg×9.8ms–2×6m
=588J.
The potential energy is 588 J.
EXAMPLE 8
An object of mass 12 kg is at a certain height above the ground. If the potential energy of the object is 480 J, find the height at which the object is with respect to the ground. Given, g=10ms–2.
Mass of the object, m=12kg,
potential energy, Ep=480J.
Ep=mgh
480J=12kg×10ms–2×h
h=480J120kgms−2=4m.
The object is at the height of 4m.
EXAMPLE 9
A rocket is moving up with a velocity v. If the velocity of this rocket is suddenly tripled, what will be the ratio of two kinetic energies?
Given, v1=vandv2=3v
∴Kinetic energy of rocket(K)=12mv2
The ratio of two kinetic energies, K1K2=v21v22(putv2=3vandv1=v)
we get =v2(3v)2=v2gv2⇒K1K2=19
Thus, the ratio of two kinetic energies K1:K2=1:9
EXAMPLE 10
(a) Can any object have mechanical energy even if its momentum is zero?
(b) Can any object have momentum even if its mechanical energy is zero?
(a) Since, mechanical energy is the sum of kinetic energy and potential energy.
And as given that, momentum of the body is zero, it means velocity of the body is zero, so it has kinetic energy equals to zero. But it may have potential energy.
So, even if the momentum of the body is zero, it may have mechanical energy.
(b) Since, mechanical energy = potential energy + kinetic energy if mechanical energy = 0
So, PE+KE=0
⇒PE=−KE
So, we can say that body may have momentum, in case mechanical energy is zero.
POWER (Rate of Doing Work)
Kya hum sab same rate pr kaam krte hain? Kya machines same rate pr energy consume or transfer krti hain? Kitne samay me kitna kaam kiya gya hai usse power kahte hai. Stronger persons jo hote hain wo koi kaam krne me km time lagate hain. Ek powerful vehicle ek less powerful vehicle ke comparison me km time me journey complete kr leti hai. Ek particular given time me jitna work kiya gya hai usse power kahte hain. Jab kaam ko krne me jyada time lagta hai, to power km hota hai aur jab kaam ko krne me km time lagta hai toh power km hota hai. Work done per unit time is called power.
The rate of doing work is called power. Power scalar quantity hai.
Measurement of power :
Ager work W hai aur time t hai to
Power P= (Work done W)/ (Time taken t)
P=Wt
Power spent by a source depends on the following two factors;
1. The amount of work done by the source, and
2. The time taken by the source to do the said work.
UNITS OF POWER
Power ka S.I. unit watt (W) hai.
1 watt= 1 joule / 1 second
Power ka bigger unit kilowatt (kW), megawatt(MW) aur gigawatt(GW) hai.
C.G.S. UNIT : Power ka C.G.S unit erg hai.
OMR (One Minute Revision)
- * Power depends on the time in which the energy is spent and time taken by the source to do the said work.
* If a person or a machine does a given amount of work in less time, more power is spent by it.
POINT 3
Power :
The rate of doing work is called power.
EXAMPLE 11
Two girls, each of weight 400 N climb up a rope through a height of 8 m. We name one of the girls A and the other B. Girl A takes 20 s while B takes 50 s to accomplish this task. What is the power expended by each girl?
(i) Power expended by girl A:
Weight of the girl, mg=400N
Displacement (height), h=8m
Time taken, t=20s
From Eq.,
Power,P=Work donetime taken
=mght
=400N×8m20s
=160W.
(ii) Power expended by girl B:
Weight of the girl, mg=400N
Displacement (height), h=8m
Time taken, t=50s
Power, P=mght
=400N×8m50s
=64W.
Power expended by girl A is 160 W.
Power expended by girl B is 64 W.
EXAMPLE 12
A boy of mass 50 kg runs up a staircase of 45 steps in 9 s. If the height of each step is 15 cm, find his power. Take g=10ms–2.
Weight of the boy,
mg=50kg×10ms–2=500N
Height of the staircase,
h=45×15100m=6.75m
Time taken to climb, t=9s
From Eq., Power,P=Work donetime taken
=mght
=500N×6.75m9s
=375W.
Power is 375 W.
EXAMPLE 13
An electric bulb of 60 W is used for 6 h per day. Calculate the ‘units’ of energy consumed in one day by the bulb.
Power of electric bulb =60W=0.06kW.
Time used, t=6h
Energy=power×time taken
=0.06kW×6h
=0.36kWh
=0.36‘units’.
The energy consumed by the bulb is 0.36 ‘units’.
EXAMPLE 14
Avinash can run with a speed of 8ms−1 against the frictional force of 10 N and Kapil can move with a speed of 3ms−1 against the frictional force of 25 N. Who is more powerful and why?
Given, force applied by Avinash=10N
Speed of Avinash=8ms−1
∴Power of Avinash=8ms−1
Now,force applied by Kapil=25N
Speed of Kapil=3ms−1
∴Power of Kapil=F.v=25×3=75W
Since, Avinash has more power (80-75)=5W then Kapil. SO Avinash is more powerful.
EXAMPLE 15
The power of a motor pump is 2 KW. How much water per minute, the pump can raise to a height of 10 m? [given,g=10ms−1]
Given, power of a motor =2KW=2×1000W=2000W [∵1KW=1000W]
Power,P=EnergyTime
By putting the values, P=mght [m=mass of water]
2000=m×10×1060 [Here,h=10mandt=1min=60s]
⇒m=2000×6010×10
m=1200kg.
Key Formulas
* W = force × displacement =mgh Joule
* Total energy (ME) = KE + PE
* PE=mgh Joule
* 'KE=1/2mv^2' Joule
* K+ U= constant
* P=Wt Watt
SUMMARY
* Work done on an object is defined as the magnitude of the force multiplied by the distance moved by the object in the direction of the applied force. The unit of work is joule: 1 joule = 1 newton × 1 metre.
* Work done on an object by a force would be zero if the displacement of the object is zero.
* An object having capability to do work is said to possess energy. Energy has the same unit as that of work.
* An object in motion possesses what is known as the kinetic energy of the object. An object of mass, m moving with velocity v has a kinetic energy of 12mv2.
* The energy possessed by a body due to its change in position or shape is called the potential energy. The gravitational potential energy of an object of mass, m raised through a height, h from the earth’s surface is given by mgh.
* According to the law of conservation of energy, energy can only be transformed from one form to another; it can neither be created nor destroyed. The total energy before and after the transformation always remains constant.
* Energy exists in nature in several forms such as kinetic energy, potential energy, heat energy, chemical energy etc. The sum of the kinetic and potential energies of an object is called its mechanical energy.
* The energy used in one hour at the rate of 1kW is called 1 kWh.