MOTION for Class 9 PHYSICS
INTRODUCTION
Har din hum ye dekhte hai ki kuchh objects ruke huye aur kuchh chalte nazar aate hai. Jaise ki car ruki hui bhi hoti aur chalti hui bhi nazar aati hai.
Jab kisi object ka position samay ke sath badalta hai to use hum motion kahte hai. Lekin aisi bhi kuchh object hote hai jo ki motion me hai ya nahi, ye janne ke liye dusre chizo ki sahayta leni padhti hai. Jaise ki air motion me hai, ise hum leaves ke movement se pata kr sakte hai ki hawa chal rahi ya nahi.
Time ke sath kisi bhi object ka position change hona motion kehlata hai. Koi body chalti hui dikhai deti hai us body ko motion me kah sakte hai.
Rest and Motion
Identify the thing at rest and in motion?

Jab koi object kisi dusre object ke respect me apni position change nahi karti hai means wo rest me hai aur ager position change karti hai means motion me hai. jaise ki uper dikhaye figure me pond and tree rest me hai but side me road se doudte hua ya cycle me chalte huye boy ko trees and pond backword motion me dikhai denge. Isi tarah kisi room ki wall bhi rest me bt koi bachcha ager gol gol ghumte huye wall ko dekhe to wall moving dikhai denge.
Rest - When the position of an object with respect to other objects around it does not change we say that it is in rest.
Motion - When the position of an object with respect to other objects around it changes we say that is in motion. Motion is the phenomenon in which an object changes its position over time. Motion is mathematically described as displacement, velocity, distance, speed, acceleration and time. niche diye gaye figure me aap dekh sakte hai ki chalti hui train se plateform rest me hote hue bhi motion me and blur dikhai deta hai aur ghumta hua lattu motion me hai jo blur dikhai deta hai.

OMR (One Minute Revision)
- * To describe the position of an object we need a reference point or origin.
* An object may seem to be moving to one observer and stationary to another.
Frame of reference
Is the boy in the car moving?
Is the trees really at rest?

Car me jab boy betha hua hai to boy car ke respect me move nahi kr raha means boy car ke respect me rest me hai but ager outside se koi us boy ko dekh raha ho to, kyuki car move kr raha hai isliye bahar se dekh rahe person ke respect me boy move kar raha hai. Isi tarah ager aap bike se road me travel kr rahe ho jiske dono kinaro me trees hai to aap aage move karte ho vaise-vaise aapko trees pichhe move karte dikhenge. Aapke respect me trees moving hai but real me trees rest me hai.
Dekhne ka jagah alag alag hai isiliye position alag alag dikhai de rahi hai. Kaha se khade hoke dekh rahe hai use reference frame kahte hai.
Kisi object ki location ko describe karne ke liye jo reference point use kr rahe hai use origin kahte hai.

Train aage ja rahi hai, baher jo hai use aap aage jate dikhai de rahe jabki aap to bethe ho aage to train ja rahi hai. Aap ek jagah pe bethe ho aur train pahiyo se move kr ry hai. Kis jagah se aap observe kr rae ho chijo ko wo frame of reference hai.
Types of Motion
Straight line, Rotational, Circular, Oscillatory, random motion are the types of motion.
Jab object sidhe move karta hai use motion in straight line kahte hai. Jaise ki figure me koi fish aur koi boat move kr rahi hai wo sidhe aaghe straight move kr rahi hai.
jab koi object apne hi jagah pr gole gole ghumti hai means apne axis pr hi rotate hoti hai use rotational motion kahte hai. Jaise ki earth apne axis pr hi gole gole ghumta hai jo rotational motion ka example hai.
Kisi object ke charo taraf jab koi dusra object chakker lagata hai use circular motion kahte hai jaise ki earth sun ke charo taraf circular motion me ghumta hai.
Oscillatory motion me koi object ek point se dusre point fr dusre point se phle point me continue motion karta hai jaise ki kisi clock ka pendulam move karta hai use oscillatory motion kahte hai.
Random motion me koi bhi object kisi bhi direction me randomly move karta hai jaise ki humari body me blood sare nerves me random motion karta hai.
POINT 1
1. Rest - When the position of an object with respect to other objects around it does not change we say that it is in rest.
2. Motion - When the position of an object with respect to other objects around it changes we say that is in motion. Motion is the phenomenon in which an object changes its position over time.
3. Origin- The reference point that is used to describe the location of an object is called origin.
4. Frame of Reference - A frame of reference, or reference frame, is a perspective that one uses to determine if an object is moving.
MOTION ALONG A STRAIGHT LINE
The simplest type of motion is the motion along a straight line.
Do point ko milane wali sidhi rekha. Straight line ke along koi object move karega to use hum bolenge motion in a straight line.
Ager hum road me sidhi line me chal rahe hai to motion straight line me hoga.
Uper diye gaye fig. se hume ye pata chalta hai ek object sidhi line me travel kr raha hai jo ki apne origin point (O) se C tak fr B se hoker A tak pahuchta hai aur uske baad wo A se wapas B ki taraf travel karta hai to magnitude of displacement 35 km hai (OA - AB i.e 60-25). Isliye magnitude of displacement barabar nahi hai total path se jo ki 85 km hai (OC+CB+BA+AB i.e 25+10+25+25).
yaha hume ek aur point pr dhyan rakhna hai ki jab object apne origin point ‘O’ se ‘A’ tak travel karta hai aur uske baad wapas usi line me ‘A’ se ‘O’ ki taraf aata hai tab total distance travel by object is 120 km hai (OA+AO i.e. 60+60), lekin yaha pr magnitude of displacement ‘zero’ hai (OA-AO), kyuki yaha pr object ki initial position equal hai final position ke.
Distance
Total length of the path travelled.Distance kabhi bhi fix nahi hota hai. Ager alag alag raste se ek shaher se dusre shaher gaye to alag alag distance ho jayenge. Distance path pe depend kr raha hai. Aap jab apne ghar se apne dost ke ghar jate hai tab aap kuchh na kuchh distance jarur cover karte hai.
Displacement
Shortest distance from initial to final position.Starting point aur end point ke bich ki sidhi duri ko dispalcement kahte hai jo kabhi change nahi hoga ye humesha fix hota hai but in case jab hume proper direction di ho tab displacement fix nahi rahegi. Displacement ke liye direction aur magnitude dono matter krti hai. Magnitude mtlb hota hai ki koi numerical value.
Vector kya hai, scalar kya hai?
Ager aap kahi travel kr rae hai aur hum aapse puchhe ki aapne kitna distance travel kiya, kitna displacement hua. Kya displacement aur distance same hai?

Maan lijiye ki niche figure me park me jo ladka initial point pr khada hai wo park ki boundary se hota hua final point tk jata hai. Uske dwara jitni duri cover ki gayi use hum distance bolenge.
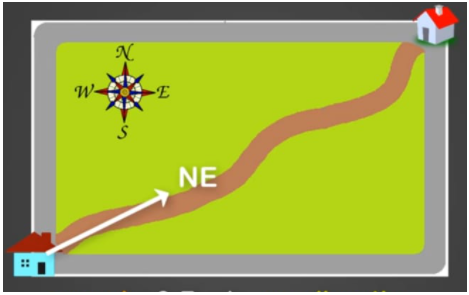
Aur ager vo sidha park ke bich se hota hua final point tak jata hai tab uske dwara cover ki gayi duri ko displacement bolenge.
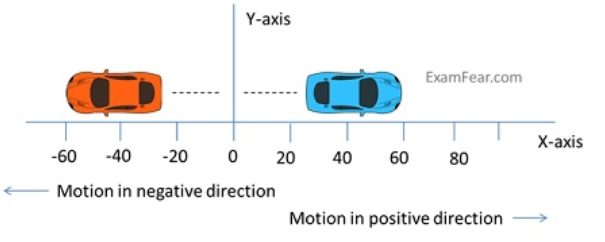
Jab koi car straight line me kisi origin point 0 se move krna star krti hai to uper diye gaye figure me aap dekh sakte hai ki y-axis ke right direction me motion positive direction me hoga aur left direction me motion negative direction me hoga.
EXAMPLE 1
A man travels a distance of 1.5 m towards East, then 2.0 m towards South and finally 4.5 m towards East.
(i) What is the total distance travelled ?
(ii) What is his resultant displacement ?
(i) Total distance travelled =1.5 + 2.0 + 4.5 = 8.0 m
(ii) To find the resultant displacement we should draw a map of the man's movements by choosing a convenient scale. Let 1 cm represent 1 m. Then 1.5 m can be represent by 1.5 cm long line, 2.0 m by 2.0 cm line and 4.5 m by a 4.5 cm long line.
We draw a 1.5 cm long line AB from West to East to represent 1.5 m towards East (see Figure 6). Then we draw a 2.0 cm long line BC towards South to represent 2.0 m towards South. And finally we draw a third line CD, 4.5 cm long, towards East to represent a distance of 4.5 m towards East. Now, the resultant displacement can be found by joining the starting point A with the finishing point D. Thus, the line AD represents the final displacement of the man. Let us measure the length line AD. It is found to be 6.3 cm.
Now, 1 cm = 1 m
So, 6.3 cm = 6.3 m
Thus, the final displacement as represented by AD is 6.3 metres. 
EXAMPLE 2
A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
Given, side of the square field = 10 m
Therefore, perimeter = 10m×4=40m
Farmer moves along the boundary in 40s
Time = 2 minutes 20 s = 2×60s+20s=140s
since, in 40s farmer moves 40m
Therefore, in 1s distance covered by farmer = 40/40 = 1m.
Therefore, in 140s distance covered by farmer = 1×140m=140m
Now, number of rotation to cover 140 along the boundary =Total distancePerimeter
= 140 m/40 m = 3.5 rounds
Thus after 3.5 rounds farmer will be at point C of the field.
Therefore, Displacement AC=√(10m)2+(10m)2
= √100m2+100m2
= √200m2
= 10√2m
= 10×1.414 = 14.14m
Thus, after 2 min 20 seconds the displacement of farmer will be equal to 14.14 m north east from initial position.
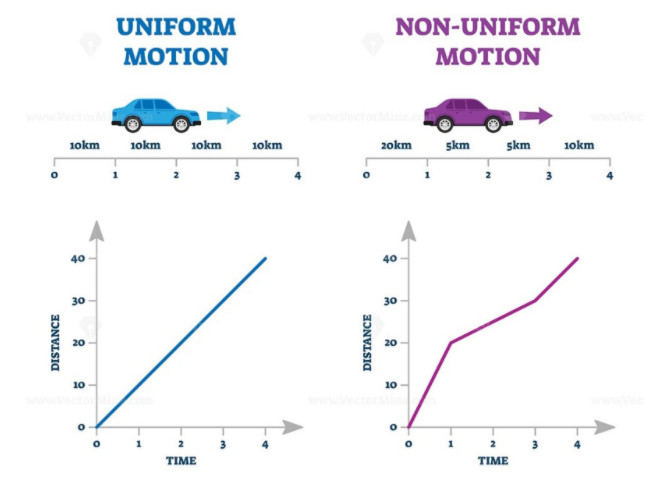
UNIFORM MOTION AND NON UNIFORM MOTION
Uniform motion
The object covers equal distances in equal intervals of time.Koi bhi object barabar time me barabar distance travel karta hai. Jaise eg. jab koi object 2 sec me 4m travel karta hai fir agle 2 sec me 4m fir agle 2 sec me 4m fir agle 2 sec me 4m mtlb yaha pr object hr 2 sec me 4m move kr raha hai to ise uniform motion kahte hai.
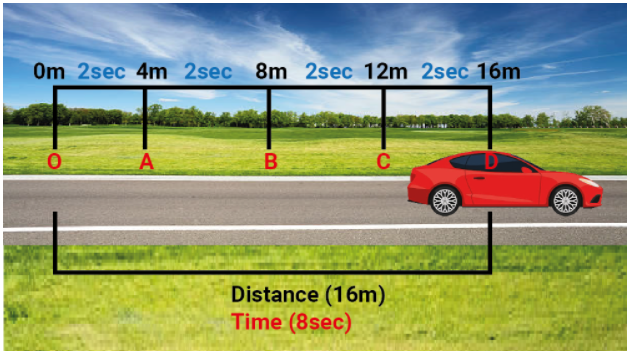
Non Uniform motion
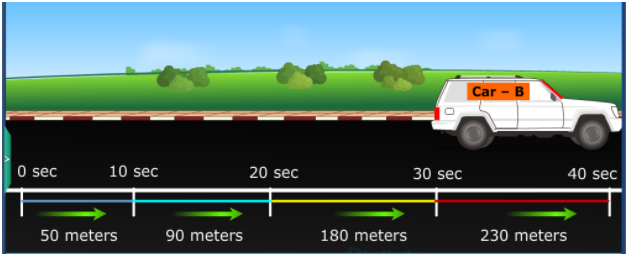
The object travels unequal distances in equal intervals of time.Eg. freely falling body
Jab koi body alag alag distance same time interval me travel karti hai tab use non-uniform motion kahte hai. Jaise eg. jab koi car 10 sec me 50m travel karta hai fir agle 10 sec me 40m fir agle 10 sec me 90m fir agle 10 sec me 50m mtlb yaha pr object hr 10 sec me different distance move kr raha hai to ise non-uniform motion kahte hai.
Niche diye gaye figure me uniform motion aur non uniform motion me comparition graphical form me show kiya gaya hai. Uniform motion ka graph hamesha straight line hota hai. Non-uniform motion ka graph straight line nahi hota.
SPEED WITH DIRECTION (Velocity)
Speed
Jo duri di gayi hai use alag alag object alag alag time me puri karte hai. Kuchh object jyada tezi se move karte hai to kuchh km speed se, aur kai object ek hi rate (speed, acceleration) se travel karte hai.Kisi bhi object ka ‘rate of motion’ ko janne ke liye to hume ye pata karna hoga ki us object ne kitne duri ek unit time me travel kiya hai. Is rate of motion ko hum speed kahte hai.
Speed=Distance/Time
Unit of Speed is :-
- SI unit of speed is meter/sec.
- cm/sec
- Km/sec.
- To specify the speed of an object, we require only its magnitude. (yaha pe speed of object constant hona chahiye).
Speed = kitne distance chale kitne time me vo hai speed
m/s mtlb ek second me kitne meter chalta hai.

Ager lagatar 40km/hr ki speed se chali gadi iska mtlb hai ki aap ek ghante me 40 km chal loge ye hai speed ka mtlb. Speed se bht sare formula bna skte hai. Kitne ki speed se bike chalae ki do ghante me 200 km pahuch jaye uske liye formula hai.
Speed=Distance/Time
Average Speed
Average speed ka mtlb jab kisi bhi object ne jitna distance travel kiya hai jitne samay me uska mean value ko average speed kahte hai.If an object travels a distance ‘s’ in time ‘t’ then its speed ‘v’ is:
Average Speed (v)= Total distance travelled (s)/Total time taken (t) i.e. v=st
Eg. ek car 2 hour me 100km distance travel karti hai. Avg. speed 50km/hr pr yaha pe car hamesha 50km/hr ki speed me nahi chala hoga, kabhi ye car in 2 hrs me 50km/hr se jyada tej bhi chali hogi aur km speed me bhi.
Velocity
Kisi bhi object ki speed ke sath sath usi direction bhi define ho to use velocity kahte hai. ye ek vector quantity hai.Vector means wo quantity jiske liye magnitude (koi numerical value) aur direction dono define ho and scalar means wo quantity jiske liye only magnitude define ho.
Velocity=Displacement/Time
Average Velocity
Agar koi object ek hi direction me alag alag speed se chal rahi hai to uske rate of motion ke magnitude ko Average velocity kahte hai.Average velocity=(initial velocity+final velocity)2
Vavg=u+v2
u= initial velocity
v= final velocity
POINT 2
Uniform Motion : When an object covers equal distances in equal intervals of time, it is said to be in uniform motion.
Non Uniform Motion : A body is said to be in a non uniform motion if it travels unequal distances in equal intervals of time.
Speed : The distance travelled by an object in unit time is referred to as speed.
Average Speed : The average speed of an object is obtained by dividing the total distance travelled by the total time taken.
Velocity : The speed of an object in a particular direction is called velocity.
Average velocity : It is the rate at which an object changes its position from one place to another.
EXAMPLE 3
A scooterist covers a distance of 3 kilometres in 5 minutes. Calculate his speed in:
(a) centimetres per second (cm/s)
(b) metres per second (m/s)
(c) kilometres per hour (km/h)
(a) In order to calculate the speed in centimetres per second we should convert the given distance of 3 kilometres into centimetres and the given time of 5 minutes into seconds. Pleas note that 1 kilometre has 1000 metres and 1 metre has 100 centimetres. Now,
Distance travelled = 3 km
=3×1000m
=3×1000×100 cm ...(1)
= 300,000 cm
Time taken = 5 minutes
=5×60 seconds
=300s ...(2) ltBrgt We know that, Speed = Distance travelledTime taken
=300,000300s
= 1000 cm/s ...(3)
Thus, the speed of scooterist is 1000 centimetres per second.
(b) In order to express the speed in metres per second we should convert the given 3 kilometres into metres and the given time of 5 minutes into seconds. Thus, in this case :
Distance travelled = 3km
=3×1000 m
=3000 m ...(4)
Time taken = 5 minutes
=5×60 seconds
= 300 s ...(5)
Now, Speed = Distance travelledTime taken
=3000m300s
=10 m/s
So, the speed of scooterist is 10 metres per second.
(c ) And finally, in order to calculate the speed in kilometres per hour, we should express the given distance in kilometres (which is already so), and the given time in hours. So, in this case :
Distance travelled = 3 km ...(7)
Time taken = 5 minutes
=560 hours
= 0.083 h ...(8)
We know that, Speed = Distance travelledTime taken
=3km0.083h
= 36 km/h ...(9)
Thus, the speed of scooterist is 36 kilometres per hour.
EXAMPLE 4
The train 'A' travelled a distance of 120 km in 3 hours whereas another train 'B' travelled a distance of 180 km in 4 hours. Which train travelled faster ?
In order to solve this problem k, we have to calculate the speeds of both the trains separately.
The train having higher speed will have travelled faster.
(i) We know that : Speed = Distance travelledTime taken
Now, Distance travelled by train A = 120 km
And, Time taken by train A = 3 h
So, Speed of train A = 120km3 h
= 40 km/h ..(1)
Thus, the speed of train A is 40 kilometres per hour.
(ii) Again, Speed=Distance travelledTime taken
Now, Distance travelled by train B = 180 km
And, Time taken by train B = 4 h
So, Speed of train B = 180 km4 h
= 45 km/h ...(2)
Thus, the speed of train B is 45 kilometres per hour.
From the above calculations we find that the train A travels a distance of 40 kilometres in one hour
whereas the train B travels a distance of 45 kilometres in one hour. Since the speed of train B is higher, therefore, train B has travelled faster.
EXAMPLE 5
A car travels a distance of 200 km from Delhi to Ambala towards North in 5 hours.
Calculate (i) speed, and (ii) velocity, of the car for this journey.
(i) Speed = Distance travelledTime taken
=200 km5 h
= 40 km/h
Thus, the speed (or average speed) of the car is 40 km/h.
(ii) Velocity = DisplacementTime taken
= 200 km towards North5 h
= 40 km/h towards North
So, the velocity (or average velocity) of the car is 40 km/h towards North.
EXAMPLE 6
A bus covers a distance of 250 km from Delhi to Jaipur towards West in 5 hours in the morning and returns to Delhi in the evening covering the same distance of 250 km in the same time of 5 hours. Find (a) average speed, and (b) average velocity, of the bus for the whole journey.
(i) Average = Total distance travelledTotal time taken
=250 km+250 km5 h+5 h
=500 km10 h = 50 km/h
Thus, the average speed of the bus fot the whole journey (both ways) is 50 kilometres per hour.
(ii) In this case, the bus travels 250 km from Delhi to Jaipur towards West and then comes back to the starting point Delhi in the reverse direction. So, the total displacement (or total distance travelled in a specified direction) will be 250 km - 250 km = 0 km. Now,
Average velocity = Total displacementTotal time taken
= 250km−250km5h+5h
=0km10h
= 0 km/h
Thus, the average velocity of the bus for the whole journey (both ways) is 0 kilometres per hour. No direction can be stated in this case of zero velocity.
EXAMPLE 7
An object travels 16 m in 4 s and then another 16 m in 2 s. What is the average speed of the object?
Total distance travelled by the object
= 16 m + 16 m = 32 m
Total time taken = 4 s + 2 s = 6 s
Average speed=Total distance travelledtotal time taken
=32m6s=5.33ms−1
Therefore, the average speed of the object is 5.33ms−1.
EXAMPLE 8
The odometer of a car reads 2000 km at the start of a trip and 2400 km at the end of the trip. If the trip took 8h, calculate the average speed of the car in km h−1 and ms−1.
Distance covered by the car,
s = 2400 km – 2000 km = 400 km
Time elapsed, t = 8 h
Average speed of the car is,
vav=st=400km8h
=50Kmh−1
=50kmh×1000m1km×1h3600s
=13.9ms−1
The average speed of the car is 50kmh−1 or 13.9ms−1.
EXAMPLE 9
Usha swims in a 90 m long pool. She covers 180 m in one minutes by swimming from one end to the other and back along the same straight path. Find the average speed and average velocity of Usha.
Total distance covered by Usha in 1 min. is 180 m.
Displacement of Usha in 1 min = 0 m
Average speed =Total distance coveredTotal time taken
=180m1min=180m1min×1min60s
Average velocity=DisplacementTotal time taken
=0m60s
=0ms−1
The average speed of Usha is 3 ms−1 and her average velocity is 0 ms−1.
EXAMPLE 10
A car travels 30 km at a uniform speed of 40 km/h and the next 30 km at a uniform speed of 20 km/h. Find its average speed.
(i) First the car travels a distance of 30 kilometres at a speed of 40 kilometres per hour. Let us find out the time taken by the car to travel this distance.
Here, Speed = 40 km/h
Distance = 30 km
And, Time = ? (To be calculated)
We know that, Speed = Distance Time
So, 40 = 30Time
And, Time = 3040 hours
Or Time (t1) = 34 hours ...(1)
(ii) Next the car travels a distance of 30 km at a speed of 20 km/h. We will also find out the time taken by the car to travel this distance. In this case :
Speed = 20 km/h
Distance = 30 km
And, Time = ? (To be calculated)
Again, Speed = DistanceTime ltBrgt So, 20 = 30Time
And, Time = 3020 hours
Or Time (t2) = 32 hours ...(2)
We can get the total time taken by the car for the whole journey by adding the above two time values t1andt2. Thus,
Total time taken = 34+32 hours
=3+64 hours
=94 hours ...(3)
And, Total distance travelled = 30 km + 30 km
= 60 km ...(4)
Now, Average speed = Total distance travelledTotal time taken
=60×49
=2409
= 26.6 km/h
Thus, the average speed of the car for the whole journey is 26.6 kilometres per hour.
EXAMPLE 11
A train travels at a speed of 60 km/h for 0.52 h, at 30 km/h for the next 0.24 h and then at 70 km/h for the next 0.71 h. What is the average speed of the train
In this problem, first of all we have to calculate the distances travelled by the train under three different conditions of speed and time.
(i) In the first case, the train travels at a speed of 60 km/h for a time of 0.52 hours.
Now, Speed = DistanceTime
So, 60=Distance0.52
And, Distance = 60 × 0.52
=31.2 km ...(1)
(ii) In the second case, the train travels at a speed of 30 km/h for a time of 0.24 hours.
Now, Speed= DistanceTime
So, 30=Distance0.24
And, Distance = 30 × 0.24
=7.2 km ...(2)
(iii) In the third case, the train travels at a speed of 70 km/h for a time of 0.71 hours.
Again, Speed = Distance Time
so, 70=Distance0.71
And, Distance = 70 × 0.71
= 49.7 km ...(3)
Now, from the equation (1), (2) and (3), we get :
Total distance travelled = 31.2+7.2+49.7
= 88.1 km ...(4)
And, Total time taken = 0.52+0.24+0.71
= 1.47 h ...(5)
We know that : Average speed = Total distance travelledTotal time taken
= 88.11.47
= 59.9 km/h.
RATE OF CHANGE OF VELOCITY (Acceleration)
The change in velocity of the object during any time interval is not zero. Jab koi object uniform motion me straight line me travel kr raha ho tab uski velocity time ke sath constant rehti hai. Is case me object ki velocity me change kisi bhi time me zero hi rahega. Jab koi object non-uniform motion me travel karta ho tab uski velocity badalti rahti hai. Is case me object ki velocity kisi bhi time me zero nahi hogi yahi acceleration kahlati hai. Acceleration ko ‘a’ se denote karte hai.
OMR (One Minute Revision)
- * Acceleration will be ‘+ve’ if it’s in direction of velocity.
* Acceleration will be ‘-ve’ when it is opposite to the direction of velocity.
* The SI unit of acceleration is ms2.
Uniform Acceleration
Jab velocity me hone wala change uniform rate se jaise 5 sec me 10km/h fr agle 5 sec me 20 km/h hota hai to is case me acceleration uniform acceleration kehlata hai.
Non-Uniform Acceleration
Jab velocity me hone wala change non uniform rate se jaise 4 sec me 10km/h, fr agle 4 sec me 25 km/h hota hai means velocity me changes same rate me nahi hua to is case me acceleration non-uniform acceleration kehlata hai.

Acceleration me change ager velocity ke direction me ho to use hum positive acceleration kahte hai but ager velocity ke opposite direction me change ho to use negative acceleration kahte hai.
Retardation
Retardation is nothing but a negative acceleration. Jab koi body accelerate hoti hai to us body me ya to positive direction me change hota hai ya fr negative direction me change hota hai. Accelerated body ki velocity me jab negative direction me change hota hai yahi Retardation ya fr Decceleration kehlata hai.
POINT 3
Acceleration : Change in the velocity of an object per unit time. Where : v is final value
u is initial value.
Uniform Acceleration : If an object's speed (velocity) is increasing at a constant rate then we say it has uniform acceleration. Uniform acceleration is change of equal velocity in equal intervals of time.
Non Uniform Acceleration : Non-Uniform means that the acceleration is not uniform. Non Uniform acceleration is change of non-equal velocity in equal intervals of time.
Retardation : The velocity of the body may either increase or decrease. The change in velocity is known as acceleration. Retardation is acceleration with a negative sign. Or the negative value of acceleration shows that the velocity of a body is decreasing.
EXAMPLE 12
Starting from a stationary position, Rahul paddles his bicycle to attain a velocity of 6 ms−1 in 30 s. Then he applies brakes such that the velocity of the bicycle comes down to 4 ms−1 in the next 5 s. Calculate the acceleration of the bicycle in both the cases.
In the first case :
Initial velocity , u=0,
Final velocity, v=6ms−1 ,
time, t=30s
From eq. (3), we have
a=v−ut
Substituting the given values of the v,u and t in the above equation, we get
a=(6ms−1−0ms−1)30s
=0.2ms−2
In the second case :
Initial velocity , u=6ms−1 ,
time, t=5s .
Then , a=(4ms−1−6ms−1)5s
=0.4ms−2
The acceleration of the bicycle in the first case is 0.2ms−2 and in the second case, it is −0.4ms−2.
EXAMPLE 13
A driver decreases the speed of a car from 25 m/s to 10 m/s is 5 seconds. Find the acceleration of the car.
First of all we should note that in this problem the term 'speed' is being used in the same sense as 'velocity'.
Here, Initial velocity of car, u = 25 m/s
Final velocity of car, v = 10 m/s
And, Time taken, t = 5s
Now, putting these values in the formula for acceleration :
a=v−ut
We get: a=10−255m/s2
a=−155m/s2
a=−3m/s2
Thus, the acceleration of car is, −3m/s2 (minus 3 m/s2). The negative sign of acceleration means that it is retardation. So, we can also say that the car has a retardation of +3m/s2 .
GRAPHICAL REPRESENTATION OF MOTION
Kisi bhi event ke graphical representation se hum us event ki basic information pata kar lete hai.
Eg. one day cricket match run rate aur over ke graph se hume ye pata chal jata hai ki kaun se over me team ka run rate kitna hai.
DISTANCE–TIME GRAPHS
The change in the position of an object with time.
Jab kisi bhi object ke position me time ke sath change ho to is relation ko hum distance-time ke graph me dikha sakte hai. Yaha pr ‘Y’ axis me hum distance ko uniformally batenge aur ‘X’ axis me time intervals ko uniformllay tarike se likha jata hai. Dist-time graph ka use in cases me hota hai
- Case 1 : Jab object ek hi speed me move kar rahi ho yani uniform speed ho tab.
- Case 2 : Jab object non uniform speed yani ki alag alag speed me move kar ho tab.
- Case 3 : Jab koi object rest me ho.
Graphically representation of cases :
case I : Uniform Speed.
Hum jante hai ki jab object equal distance travel karta hai equal time aur ek hi speed me chalte hai is se hume ye pata chalta hai ki distance travelled by the object is directly proportional to the time taken.
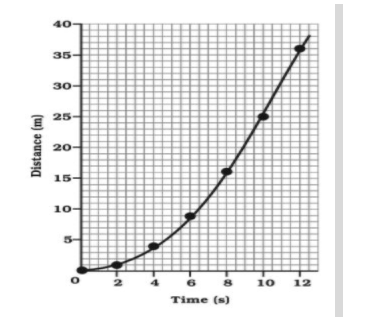
Case II : Non-Uniform Speed
Is graph me yeh show ho raha ki object variable speed se distance cover kar raha hai, yeh motion dikhta hai ye non-uniform speed hai.
VELOCITY-TIME (SPEED-TIME) GRAPHS
The variation in velocity with time for an object moving in a straight line.
Case : I Uniform Motion : (Constant velocity)
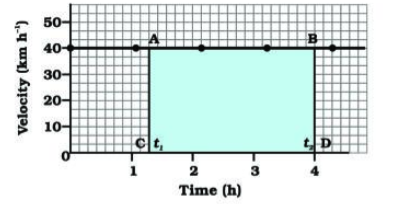
It will be a straight line parallel to the x-axis.The variation of velocity with time for an object moving in a straight line represents velocity-time graph.
Jab koi object (car) ek hi velocity me straight line me chal raha hai. Then, us object ka velocity-time graph aisa hoga :
Uniformly Accelerated Motion (Velocity changes with uniform Rate) :
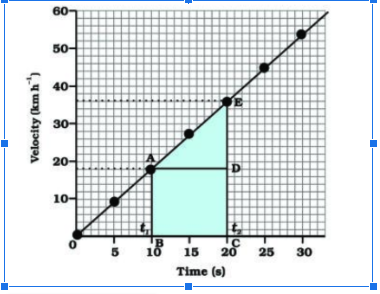
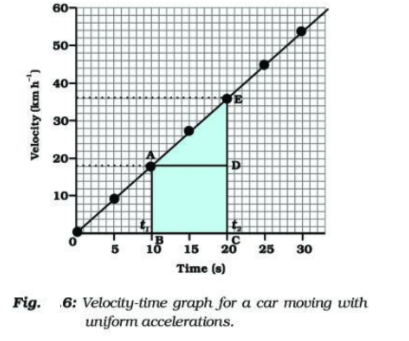
Velocity changes by equal amounts in equal intervals of time. Thus, for all uniformly accelerated motion, the velocity-time graph is a straight line.Is graph sai hume ye pata chal raha hai ki ek car 40Km/hr ki raftar se chal rahi hai.
⇒ Is graph me car ki velocity me increase ho rahi hai equal interval of time ke sath. Is graph me hum ye dekh sakte hai ki car ki velocity har ‘5sec’ me increase ho rahi hai.
Is graph se hum ye bhi pata kar sakte hai ki car ne kitni duri tavel ki hai.
For eg. Hum point ’A’ sai ‘E’ ka displacement kaise niklange?
Pehle hum point ‘AE’ ko x-axis sai join kar lete hai is se hume us points ka area mitla hai jo ki [s=ABCDE] hai. i.e. s = area of rectangle(ABCD)+ area of Triangle(ADE).
⇒ s=(AB×BC)+½(AD×DE).
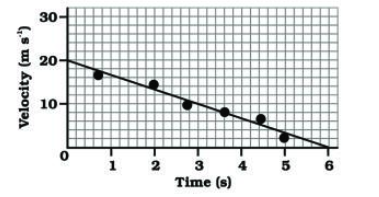
Case : II Non Uniform Acceleration (Velocity changes with non-uniform Rate) :
⇒ Is graph se hume ye pata chalta hai ki car ki velocity time ke sath decrease ho rahi hai.
In the case of non-uniformly accelerated motion, velocity-time graphs can have any shape.
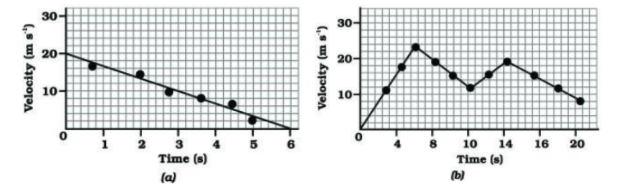
⇒ Is graph se hume ye pata chalta hai ki car ki velocity non-uniform hai car ke time ke sath.
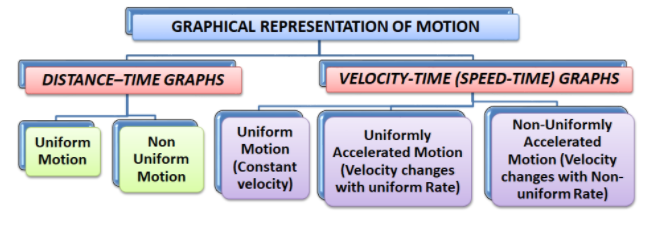
POINT 4
Distance-Time Graph : The change in the position of an object with time
Velocity-time (Speed-time) Graph : The variation in velocity with time for an object moving in a straight line.
EXAMPLE 14
What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
If the distance time graph is a straight line parallel to the time axis, the body is said to be at rest.
EXAMPLE 15
Study the speed-time graph of a body given here and answer the following questions :
(a) What type of motion is represented by OA ?
(b) What type of motion is represented by AB ?
(c ) What type of motion is represented by BC ?
(d) Find out the acceleration of the body.
(e) Calculate the retardation of the body.
(f) Find out the distance travelled by the body from A to B.
(a) Oa is a straight line graph between speed and time, and it is sloping upwards from O to A. Therefore, the graph line OA represents uniform acceleration.
(b) AB is a straight line graph between speed and time, which is parallel to the time axis (x-axis). So, AB represents uniform speed (or constant speed). There is no acceleration from A to B.
(c) BC is a straight line graph between speed and time which is sloping downwards from B to C. Therefore, BC represents uniform retardation (or negative acceleration).
(d) Let us find out the acceleration now. We have just seen that the graph line OA represents acceleration.
So, the slope of speed-time graph OA will give us the acceleration of the body. Thus,
Acceleration = Slope of line OA
=ADOD
Now, in the given graph (Figure 40), we find that AD = 6 m/s and OD = 4 seconds. So, putting these values in the above relation, we get :
Acceleration = 6m/s4s
= 1.5 m/s2 ...(1)
(e) Let us calculate the retardation now. We have discussed above that the graph line BC represents retardation. So, the slope of speed-time graph BC will be equal to the retardation of the body. So,
Retardation = Slope of line BC
=BEEC
Now, in the graph given to us (Figure 40), we find that BE = 6 m/s and EC = 16-10=6 seconds. So, putting these values in the above relation, we get :
Retardation = 6m/s6s
= 1 m/s2 ...(2)
(f) We will now find out the distance travelled by the body in moving from A to B (Figure 40). We have studied that in a speed-time graph, the distance travelled by the body is equal to the area enclosed between the speed-time graph and the time-axis. Thus,
Distance travelled from A to B = Area under the line AB and the time axis
= Area of rectangle DABE
=DA×DE
Now, from the given graph (Figure 40), we find that DA = 6 m/s and DE = 10 -4 = 6 s. Therefore,
Distance travelled from A to B = 6×6
= 36 m

EQUATIONS OF MOTION BY GRAPHICAL METHOD
Jab koi object straight line me move karta uniform acceleration ke sath tab ye possible hai ki us object ka motion ke duration me hum acceleration, velocity, distance aur time calculate kr sakte hai. Ise calculate karne ke liye hamare pas 3 equation hai.
Humne jo straight line me ho rahe motion ke bare me padha usme humne distance, velocity and uniform acceleration ko smjha jo ki object ke kuchh time tak motion me rahne ke baad hume mil raha tha. Ab agar hum in physical quantities ko aapas me corelate krna chahe to uske liye object ke initial aur final position ke bich distance time graph and velocity time graph ka use karke kuchh equations find out kiye gaye. Inhi set of equations ko hum equation of motion kahte hai. In motion ke equation ko hum derivations aur graph dono se find kr skte hai. Yaha pr hum dekhenge ki graph ke help se kaise equation find kiye gaye. Equations of motion ke liye 3 equation nikale gaye joki is prakar hai :
v=u+at.............. (i)
s=ut+12at2.... (ii)
2as=v2−u2..... (iii)
Uper diye gaye equation me 'u' initial velocity hai, mtlb object ki starting point me jo velocity hogi wo & 'v' final velocity hai mtlb ki object ke end point pr jo object ki velocity hogi wo, 'a' yaha pe uniform acceleration hai jo ki, 't' time me object ke motion me rahne ki vajah se velocity me ho rahe lagatar change ki wajah se hume milegi. Time 't' me object jitna distance travel kr ry hai mtlb jitni duri chal ry hai us distance ko hum 's' se show kr rahe hai.

Motion k lie equation :
(i) Hume velocity aur time ke bich relation find out krne se milega equation.
(ii) Hume position mtlb ki object ne jitna distance travel kiya aur kitne time kiya inke bich relation find karne se equation milega.
(iii) Equation jo hai wo object ki position aur velocity ke bich ka relation hai, jisko hum (equation ..i) ke help se find karenge aur fr equations me se time t ko eliminate karke, mtlb pehle equation se t ki value nikal ke dusre equation me t ke jagah rakh ke find kiya jayega.
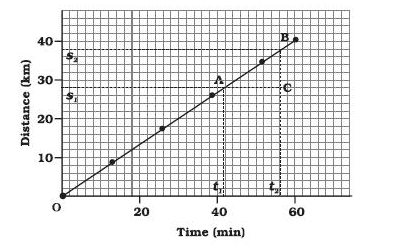
Uper diye gaye graph me ager aap khud ko assume krke 'P' point se uniform velocity se chalna start kare, jisme jab aap chalna start krte hai us time aapki velocity u (OP) ho wo aapki initial velocity hogi. Kyuki aap jis velocity se aage chal rahe ho us velocity me changes equal amount me equal interval of time ho rahe hai isiliye acceleration uniform hoga aur aap straight line me point N tk chaloge tb final point N pr aapki velocity v (NR) hogi. Point 'P' se 'N' tk aap s distance chale jisme aap uniform acceleration a se aage badhe or aapko travelling me t (OR=PQ) time laga.
EQUATION FOR VELOCITY-TIME RELATION
Uper diye gae graph se ager hum velocity aur time ke bich relation nikale to velocity v means NR jo ki NQ aur QR ke addition ke barabar hoga.NR=NQ+QR
QR parallel hai PO ke aur baraber bhi hai and PO ki value hai jise humne initial velocity liya tha. Isliye hum QR ke jagah PO rakh skte hai to equation ho jaega :
NR=NQ+PO
Ab kyuki PO ki value 'u' hai or NR ki value 'v' hai to uske jagah eq. me hum u rakh dete hai.
v=NQ+u
Yaha hume NQ ki value nikalni hai jisko hum graph me diye gaye slope jo ki uniform acceleration a hi hai aur PQ ka use krke nikal skte hai. Right angle triangle se slope (PN) ki value hogi.
a=slope of line(PN)=NQPQ
Yaha per PQ parallel hai OR ke jo ki t time ko show kr raha hai. Isliye PQ ki jagah t put krne pr a=NQt ho jayega.
Ab NQ=at se hume NQ ki value mil gayi jise hum eq. me put krte hai to velocity aur time ke bich relation hoga.
v=at+u
Ya fir v=u+at
Ye eq. Motion ke liye first eq. hai jo velocity aur time ke bich ka relation hai.
EQUATION FOR POSITION-TIME RELATION
Motion ka dusra eq. Nikalne ke liye hum aapke dwara chale gaye 's' distance jo 't' time me travel krta hai inke bich relation find karenge.Graph me uniform acceleration PN aur time OR ke bich ka space niaklne ke liye hum iske dwara cover kiye ja rahe area ko calculate karenge to hume graph me position (s) aur time (t) ke bich relation mil jaega.
s = area OPNR (which is a trapezium)
= area of the rectangle OPQR + area of the triangle PNQ
=OP×OR+12(PQ×NQ)..... (10)
Substituting OP=u, OR=PQ=t and NQ=at,
we get
s=u×t+12(t×at)
s=ut+12(at2)
EQUATION FOR POSITION–VELOCITY RELATION
Graph me uniform acceleration PN aur time OR ke bich ka space nikalne ke liye hum iske dwara cover kiye ja rahe area ko humne jis tarah position aur time ke bich relation find krne ke liye rectangle aur triangle ka area nikal ke add kr diya uske jagah hum ager direct trapezium ka area nikale to hume position aur velocity ke bich relation mil jayega.s = area of the trapezium OABC
= (OA + BC × OC)/2
Substituting OA=u, BC=v and OC=t, we get
s=(u+v)t2...... (11)
From the velocity-time relation ( motion ka first eq.),
we get
t=v−ua.... (12)
Using Eqs. (11) and (12) we have,
s=(v+u)(v−u)2a
or 2as=v2−u2
or v2=u2+2as
POINT 5
Equations of Motion : An object moves along a straight line with uniform acceleration, it is possible to relate its velocity, acceleration during motion and the distance covered by it in a certain time interval by a set of equations known as the equations of motion.
EXAMPLE 16
A car travelling at 20 km/h speeds up to 6 km/h in 6 seconds. What is its acceleration ?
Here, Initial speed, u = 20 km/h
=20×1000 m60×60 s
=5.55m/s …(1)
Final speed, v= 60 km/h
=60×1000 m60×60 s
= 16.66 m/s …(2)
Acceleration, a = ? (To be calculated)
And, Time, t = 6 s
We know that : v=u+at
So, 16.66=5.55+a×6
6a=16.66−5.55
6a=11.11
a=11.116
Thus, Acceleration, a = 1.85 m/s2.
EXAMPLE 17
A body starts to slide over a horizontal surface with an initial velocity of 0.5 m/s. Due to friction, its velocity decreases at the rate of 0.05 m/s2 (acceleration, -0.05 m/s2). How much time will it take for the body to stop ?
Here, Initial velocity, u = 0.5 m/s
Final velocity, v = 0 (The body stops)
Acceleration, a = -0.05 m/s2
And, Time, t = ? (To be calculated)
Now, from the first equation of motion, we have :
v=u+at ltBrgt So, 0=0.5+(−0.05)×t
or 0.05t=0.5 ltBrgt t=0.50.05
t=10s
Thus, the body will take 10 seconds to stop.
EXAMPLE 18
A train starting from rest attains a velocity of 72 km h−1 in 5 minutes. Assuming that the acceleration is uniform, find (i) the acceleration and (ii) the distance travelled by the train for attaining this velocity.
We have been given
u=0,v=72kmh−1=20ms−1 and t=5 minutes =300s
(i) From Eq. (5) we know that
a=(v−u)t
=20ms−1−0ms−1300s
=115ms−2
(ii) From Eq. (7) we have 2as=v2−u2=v2−0
Thus ,
s=v22a
=(20ms−1)22×(1/15)ms−2
= 3000 m =3 km
The acceleration of the train is 115ms−2 and the distance travelled is 3 km.
EXAMPLE 19
A car accelerates uniformly from 18 km h−1 to 36 km h−1 in 5 s. Calculate (i) the acceleration and (ii) the distance covered by the car in that time.
We are given that
u=18 kmh−1=5ms−1
v=36kmh−1=10ms−1 and
t=5 s.
(i) From Eq. (5) we have
a=v−ut
=10ms−1−5ms−15s
=1ms−2
(ii) From Eq. (6) We have
s=ut+12at2
=5ms−1×5s+12×1ms−2×(5s)2
=25m+12.5m
=37.5 m
The acceleration of the car is 1 ms−2 and the distance covered is 37.5 m.
EXAMPLE 20
The brakes applied to a car produce an acceleration of 6 m s−2 in the opposite direction to the motion. If the car takes 2 s to stop after the application of brakes, calculate the distance it travels during this time.
We have been given
a=−6ms−2,t=2s and v=0ms−1
From Eq. (5) we know that
v=ut+at
0=u+(−6ms−2)×2s
or u=12ms−1 .
From Eq. (6) we get
s=ut+12at2
=(12ms−1)×(2s)+12(−6ms−2)(2s)2
=24m−12m
=12 m
Thus, the car will move 12 m before it stops after the application of brakes.
EXAMPLE 21
A stone is thrown in a vertically upward direction with a velocity of 5 m s−1. If the acceleration of the stone during its motion is 10 m s−2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
Given initial velocity of stone, u = 5 m s−1
Downward of negative Acceleration, a = 10 m s2
We know that 2as=v2−u2
Therefore, Height attained by the stone, s=0252×(−10)m
=−25−20m
= 1.25 m
Also we know that final velocity, v = u + at
or, Time, t=v−ua
Therefore, Time, t taken by stone to attain the height, s 0−5−10s
= 0.5 s.
EXAMPLE 22
A scooter moving at a speed of 10 m/s is stopped by applying brakes which produce a uniform acceleration of, -0.5 m/s2. How much distance will be covered by the scooter before it stops ?
Here, Initial speed, u = 10 m/s
Final speed, v = 0 (Scooter stops)
Acceleration, a = -0.05 m/s2
And, Distance covered, s = ? (To be calculated)
Now, putting these values in the third equation of motion :
v2=u2+2as
We get : (0)2=(10)2+2×(−0.5)×s
0=100−s
s=100 m
Thus, the distance covered is 100 metres.
UNIFORM CIRCULAR MOTION
Jab koi object ek hi speed me gol ghume tab use motion ko uniform circular motion kahte hai. Eg. Earth.

Ab tak humne sikha ki jab velocity me change ho raha tha to hum kah rahe the ki body accelerate ho ry hai. Body me acceleration velocity ki magnitude (any numerical value of velocity) ya fr body ager apni direction ya velocity ke magnitude aur direction dono me change kr ry hai to body accelerate hogi.
Ager koi body kevel apni direction me change kare jabki magnitude same hi ho to iske lie kuchh examples lete hai hai. Jaisa ki niche diye gae figure me dikhaya hai ki body ager kisi rectangular path me chal ry hai to velocity body ki same rahegi jabki direction kevel char bar hi change hoga. Ager bod kisi hexagonal path me chale to velocity magnitude same hoga jabki direction me 6 times change hoga. Isi tarah hum direction me changes ko 8 times kr de to octagonal shape bangega or lagatar number of changes in direction badhte jae aur path ke hr point pe velocity ka magnitude same ho to body ek circular path me chalne lagegi.
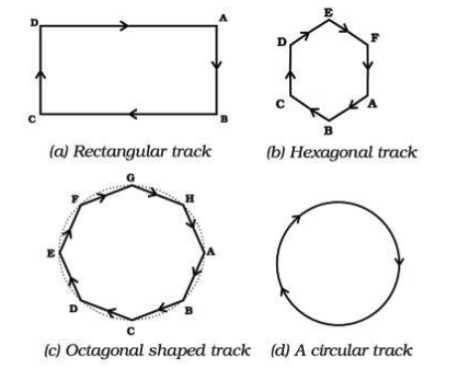
Is circular path me body ki speed uniform hai aur direction continuous variable hai. Yahi circular motion hai. Circular motion me body jab ek circle pura krta hai iska mtlb hoga ki wo circle ke circumference ke baraber distance travel kiya.
Ager hum circular path ka radius 'r' le to aur ek round pura krne me body ko 't' time lage to body ki speed ko hum is equation se pata kar sakte hai :
- v=2πrt
When an object moves in a circular path with uniform speed, its motion is called uniform circular motion.
And if a body is moved in a circle at constant velocity then it is called as Uniform circular motion.
Jab koi object circle me ek hi speed maintain karta hai tab us object ke motion ko uniform circular motion kahte hai.
Eg: Ek wheel ek hi speed me ghum raha hai. Iske alawa aur bhi circular motion ke eg. niche diye figure me aap dekh sakte hai.


POINT 6
Uniform Circular Motion : When a body moves in a circle, it is called circular motion and when it maintains its speed then it is called uniform circular motion.
EXAMPLE 23
A cyclist goes around a circular track once every 2 minutes. If the radius of the circular track is 105 metre, calculate his speed. (Given π=227)
We know that for a body moving in a circular path :
v=2πrt
Here, speed, v = ? (To be calculated)
pi,π=227
Radius of circular track, r = 105 m
And, Time taken for 1 round, t = 2 minutes
=2×60 seconds
=120 s
Now, putting these values of π,r and t in the above formula, we get :
v=2×22×1057×120
=5.5m/s
Thus, the speed of cyclist on the circular track is 5.5 metres per second.
EXAMPLE 24
The length of minutes hand of a clock is 5cm . Calculate its speed.
Here, r=5cm,v=?
Time taken by minute's hand of a clock to go once around the circle , t=60min=60×60s
From , v=2πrt=2×227×560×60=8.7×10−3cm/s.
KEY FORMULA
*v=st
*V=dt
* Vavg=u+v2
* a=v−ut
* Equation of motion
v=u+at
v2–u2=2as
s=ut+(12)at2
SUMMARY
1. Motion is a change of position; it can be described in terms of the distance moved or the displacement.
2. The motion of an object could be uniform or non-uniform depending on whether its velocity is constant or changing.
3. The speed of an object is the distance covered per unit time, and velocity is the displacement per unit time.
4. The acceleration of an object is the change in velocity per unit time.
5. Uniform and non-uniform motions of objects can be shown through graphs.
6. The motion of an object moving at uniform acceleration can be described with the help of the following equations, namely
- v=u+at
s=ut+½at2
2as=v2–u2
where u is initial velocity of the object, which moves with uniform acceleration a for time t, v is its final velocity and s is the distance it travelled in time t.
7. If an object moves in a circular path with uniform speed, its motion is called uniform circular motion.