GRAVITATION for Class 9 PHYSICS
INTRODUCTION
Aapne previous chapter me padha ki force jaruri hota hai kisi bhi body ko move krne ke liye. Iska mtlb minimum ek force jaruri hota hai ek body me motion produce krne ke liye. Ager hum kisi height se ek stone ko drop krte hai to vo stone niche gir jata hai, down towards the Earth. Iska mtlb hai ki stone motion me hai aur uspr jarur koi force act kr raha hai. This force is the force of attraction (called gravity), jo earth exert krta hai stone pr aur usko niche pull karta hai. Planets Sun ke around revolve karte hain. Moon Earth ke around revolve karta hai. In sare cases me force object pr act hota hai. So, this force is called the Gravitational Force. Is chapter me hum isi force se related gravitation aur uske laws and physical effects ke baare me study karenge.
WHAT IS GRAVITATION
Earth saare chizon ko apni taraf khichta hai, by an unseen force of attraction. Gravitation or gravity universal force of attraction hai jo sare matter ke beech act karta hai.
Earth saare objects ko attract or pull krta hai apne centre ke taraf. Ye force jisse earth objects ko pull krta hai us force ko gravitational force of earth or gravity of earth kahte hain. Earth ke uper atmosphere hold krne me, barish hone me, rivers me flow of water in sab process me gravitational force hi responsible hai.
Jaise ki eg. ager koi boy ball ko uper fekta hai fr wo ball gravitational force ke karan wapas niche hi aajata hai.

UNIVERSAL LAW OF GRAVITATION
Newton ke according, hr object is universe me hr dusre object ko attract krta hai ek certain force se.Universal Law of Gravitation Newton ne diya tha. So isliye isko Newton's Law of Gravitation bhi bolte hai. Is law ke according, hr body is universe me hr dusre body ko attract krta hai ek force se jo directly proportional hota hai unke mass ke product ke aur inversely proportional hota hai unke beech ke distance ke square ke.
The force acts along the line joining the centres of the objects.
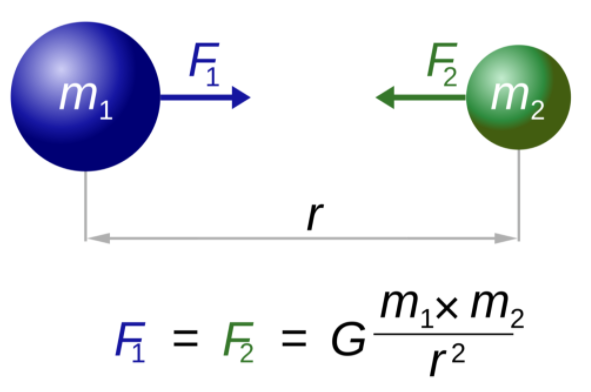
Yaha G Universal Constant hai. G is called universal constant because its value remains the same throughout the universe and is independent of masses of the objects.
To calculate the value of g
To calculate the value of g, we should put the values of G, M and R , namely, universal gravitational constant, G=6.7×10−11Nm2kg−2, mass of the earth, M=6×1024kg, and radius of the earth, R=6.4×106m.g=GMR2
=6.7×10−11Nm2kg−2×6×1024kg(6.4×106m2)2
g=9.8ms–2
Thus, the value of acceleration due to gravity of the earth, g=9.8ms−2
Importance of the universal law of gravitation
OMR (One Minute Revision)
- *Agar kisi object ka mass jyada hai to unper lagne wala gravitational force bhi jyada hoga aur agar kisi object ka mass km hai to force bhi km hoga kyuki ye force objects ke mass ke directly proportional hai.
* Agar kisi do objects ke beech ka distance jyada hai to gravitational force km lagega aur agar kisi do objects ke beech ka distance km hai to gravitational force jyada lagega kyuki ye force distance ke square ke inversely proportional hai.
POINT 1
Centripetal Force :
The force that causes this acceleration and keeps the body moving along the circular path is acting towards the centre. This force is called the centripetal (meaning ‘centre-seeking’) force.
Gravitational Force :
The force of attraction between objects is called the gravitational force.
Universal Law of Gravitation :
According to the universal law of gravitation, every object in the universe attracts every other object with a force which is proportional to the product of their masses and inversely proportional to the square of the distance between them. The force is along the line joining the centres of two objects.
EXAMPLE 1
The mass of the earth is 6×1024 kg and that of the moon is 7.4×1022 kg. If the distance between the earth and the moon is 3.84×105 km, calculate the force exerted by the earth on the moon. (Take G =6.7×10−11Nm2kg−2)
The mass of the earth, M=6×1024kg
the mass of the moon, m=7.4×1022kg
the distance between the earth and the moon, d=3.84×105km
=3.84×105×1000m
=3.84×108m
G=6.7×10−11Nm2kg−2
Gravitational force exerted by the earth on the moon is
F=GM×md2
=6.7×10−11Nm2kg−2×6×1024kg×7.4×1022kg(3.84×108m)2
=2.02×1020N
Thus the force exerted by the earth on the moon is 2.02×1020 N.
EXAMPLE 2
What happens to the force between two objects, if :
(i) The mass of one object is doubled?
(ii) The distance between the objects is (a) doubled, and (b) tripled?
(iii) The mass of both objects are doubled ?
(i) The gravitational force between two objects is directly proportional to the product of masses of the two object. So if one of the objects is doubled, then the force also gets doubled (it becomes 2 times ).
(ii) The gravitational force between two objects is inversely proportional to the square of distance between them.
(a) If the distance between two objects is doubled (made 2 times) the force becomes (12)2or14 (one - fourth ) .
(b) If the distance between two objects is tripled (made 3 times) the force becomes (13)2or19 (one - ninth ).
(iii) The gravitational force between two objects is directly proportional to the product of their masses. So, if the masses of both the objects are doubled (made 2 times each), the force between them will become 2×2= 4 times.
FREE FALL
Earth saare objects ko apne taraf attract karta hai. Ye gravitational force ke karan hota hai. Jab bhi koi object earth ke towards fall karta hai gravitational force ke karan, to hum kahte hai ki vo object free fall me hai. Jab koi object fall karta hai to kya uska velocity change hota hai? Jab object fall karta hai to uske motion me koi change nahi hota hai pr earth ke attraction ke karan, uske velocity ke magnitude me change hota hai. Kisi bhi velocity me jab change hota hai to acceleration involve hota hai. Ye acceleration earth ke gravitational force ke karan hota hai isliye ise acceleration due to gravity (g) kahte hain.
When an object falls from any height under the influence of gravitational force only, it is known as free fall.
Air resistance is a force that is caused by air, the force acts in the opposite direction to an object moving through the air.
Jab hum ek stone aur paper ko ek height se drop krte hai toh stone paper se pehle ground pr fall karta hai. Aisa isliye hota hai kyunki paper pr jyada air resistance lagta hai aur stone pr km air resistance lagta hai.
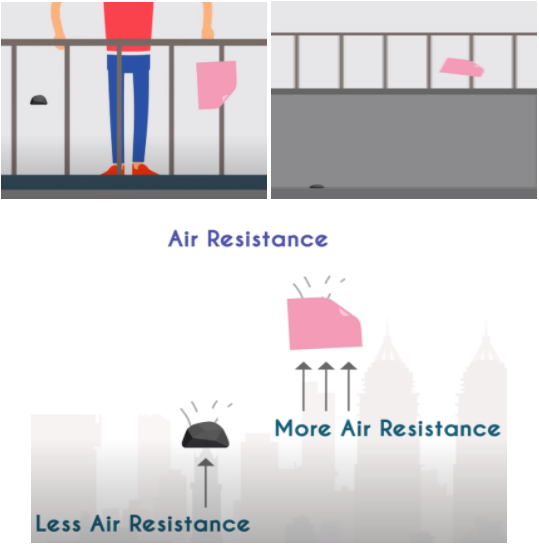
Agar ye stone aur paper ko hum drop kare in vacuum, to kya hoga? Mtlb ki koi aisi area jaha se all air remove ho gayi ho. In this case, both stone and paper will fall at the same rate, and will hit the ground at the same time. Easy calculation ke liye hum generally air resistance ko neglect kr dete hain.
MOTION OF OBJECTS UNDER THE INFLUENCE OF GRAVITATIONAL FORCE OF THE EARTH
Object acceleration experience karta hai during free fall. Ye acceleration jo object experience karta hai vo uske mass pr depend nahi karta hai. Iska mtlb ki object solid ho ya hollow ho, chhota ho ya badha ho sare same rate se fall karte hain. ‘g’ ka value earth ke pas constant ho jata hai to sare equations uniformly accelerated motion of objects acceleration a se valid ho jate hain aur g, a se replace ho jata hai.The equations are:
v=u+at
s=ut+12at2
v2=u2+2as.
Yaha, u initial velocity, v final velocity, s distance, aur t time hai. So, in all 3 equations of uniformly accelerated motion, acceleration a ko hum ‘g’ se replace kr sakte hai aur hum ‘a’ ko positive lenge kyuki vo velocity aur motion ke direction me hai. Acceleration ‘a’ will be negative agar vo direction of motion ke opposite hota hai.

ACCELERATION DUE TO GRAVITY
Jab koi object fall krta hai towards the Earth to uske acceleration me change hota hai gravitational force of Earth ke karan. This acceleration is called acceleration due to gravity.
- The acceleration due to gravity ko g se denote karte hain.
- Acceleration due to gravity g aur acceleration a dono ka unit same hai i.e., ms2.
Factors Affecting the Value of g
- Earth ka shape, altitude aur depth (below the earth's surface). In factors pr g ka value depend karta hai. Jab depth increase hota hai, acceleration due to gravity decrease ho jata hai.
- Poles pr g ka value equator se jyada hota hai kyunki equator pr earth ka radius poles ke comparison me jyada hota hai.
- Jab hum large heights pr jate hain toh g ka value decrease ho jata hai.
Relation Between G and g
From the second law of motion, force is the product of mass and acceleration.
F=ma ….(i)
For free fall, acceleration is replaced by acceleration due to gravity.
Therefore, force becomes:
F=mg ….(ii)
By universal law of gravitation
F=GMmR2 ……(1)
By Newton’s second law
F=mg ……..(2)
From eq. (1) and (2)
⇒mg=GMmR2 …….(3)
∴ g=GMR2
Here,
g = Acceleration due to gravity
G = Universal gravitational constant
R = Radius of Earth
Difference between G and g
Gravitational Force Holds The Solar System Together :
Solar System me planets circular orbits me sun ke chakkar katte hai aur satellites planets ke chakkar katte hai. Circular orbit me move karne ke liye object ko centripetal force ki jarurat hoti hai. Planets ko sun ka chakkar katne ke liye, centripetal force sun ke gravitational force se milti hai aur satellites ko planets ka chakkar katne ke liye, centripetal force planets ke gravitational force se milti hai. It is the gravitational force between the Sun and the Earth which keeps the Earth in circular motion around the sun.

KEPLER'S LAWS OF PLANETARY MOTION
First Law : Planets Sun ke around elliptical orbits me move karte hain. Ellipse ek shape hai jo flattened circle ko resemble karta hai.Planetary orbits are elliptical with the sun at a focus.
Second Law : Second law of motion se force ka value mass aur acceleration ke product ke equal hota hai.
Jab hum free fall ki baat kar rahe, toh acceleration ko acceleration due to gravity se, matlab ki 'g' se replace kiya ja sakta hai.
The radius vector from the sun to a planet sweeps equal areas in equal times.
The second law simply states "The radius vector from the Sun to a planet sweeps equal areas in equal times" mtlb radius vector jo sun se ek planet tak hota hai vo area equal cover hota hai equal time me.
Third Law : Period of revolution ka square aur ellipse semi major axis ka cube ka ratio saare planets ka same hota hai.
The ratio of the square of the period of revolution and the cube of the ellipse semi major axis is the same for all planets.
These laws can be mathematically derived in terms of Newtonian mechanics and universal gravitation.

POINT 2
Free Fall :
When an object falls towards the earth due to earth’s gravity and no other force is acting upon it, the object is said to be in free fall state.
Free-fall Acceleration :
Free falling objects are not even resisted by the air. g=9.8m/s2 is also called the Free-fall Acceleration.
EXAMPLE 3
A car falls off a ledge and drops to the ground in 0.5 s, Let g=10ms−2 (For simplifying the Calculations ),
(i) What is its speed on striking the ground ?
(ii) What is its average speed during the 0.5 s?
(iii) How high is the ledge from the ground ?
Time, t=12 second
Initial velocity, u=0ms−1
Acceleration due to gravity, g=10ms−2
Acceleration of the car, a=+10ms−2(downward)
(i) Speed, v=at
v=10ms−2×0.5s
=5ms−1
(ii) Average speed =u+v2
=(0ms−1+5ms−1)/2
=2.5ms−1
(iii) Distance travelled, s=12at2
=12×10ms−2×(0.5s)2
=12×10ms−2×0.25s2
=1.25m
Thus, (i) Its speed on striking the ground =5ms−1
(ii) Its average speed during the 0.5 s =2.5ms−1
(iii) Height of the ledge from the ground =1.25m.
EXAMPLE 4
On the earth a stone's throw from a height in a direction parallel to the earth's surface while another stone is simultaneously dropped from the same height Which stone would reach the ground first and why ?
Time taken by both stone is given second equation of motion s=ut+1/2at2
As Uy=O,S=1/2at2
andhere s=h
where, Uy = Initial velocity in y-axis
a=g acceleration due to gravity
t = time displacement to time
So, h=1/2gt2
t=√2hg
Therefore, it we drop down a stone from a height (h) and at same time throw another stone in horizontal direction, then both the stone strike the earth simultaneously at different places.
EXAMPLE 5
Identical packets are dropped from two aeroplanes, one above the equator and the other above the north pole, both at height h. Assuming all conditions are identical, will those packets take same time to reach the surface of earth. Justify your answer.
No, those packets do not take same time to reach the surface of the earth. Because the value of g (i.g., acceleration due to gravity is) different at poles and equator due to rotation of the earth and is given by g′=g−ω2rsinθ and at polesθ=0∘ whereas at equator θ=90∘. So, value of g at equator is less than value of g at poles and we know that, t=√2hgi.e.,t∝1g
Since, g is greatest at the poles than at the equator. So, packet dropped above the north pole will reach first at the surface of the earth.
EXAMPLE 6
The earth is acted upon by gravitation of the sun, even thought it does not fall into the sun. Why?
The earth revolves around the sun. The centripetal force is needed by the earth to revolve around the sun. This centripetal force is provided by the gravitational force between the sun and the earth. And this gravitational force restricts the earth to fall into the sun.
EXAMPLE 7
An object is thrown vertically upwards and rises to a height of 10m. Calculate
(i) The velocity with which the object was thrown upwards and
(ii) The time taken by the object to reach the highest point.
Distance travelled, s=10m
Final velocity, v=0ms−1
Acceleration due to gravity, g=9.8ms−2
Acceleration of the object, a=−9.8ms−1 (upward motion )
(i) v2=u2+2as
0=u2+2×(−9.8ms−1)×10m
−u2=−2×9.8×10m2s−2
u=√196ms−1
u=14ms−1
(ii) v=u+at
0=14ms−1−9.8ms−2×t
t=1.43s.
EXAMPLE 8
Calculate the value of acceleration due to gravity on the surface of the moon (given Mass of the moon =7.4×1022kg, Radius of moon =1740km and G=6.7×10−11Nm2/kg2
The formula for calculating the acceleration due to gravity is :
g=GMR2
Here Gravitational constant G=6.7×10−11Nm2/kg2
Mass of the moon, M=7.4×1022kg
Radius of the moon, R=1740km =1740×1000m = 1.74×106m
Now Putting these values of G, M and R in the above formula we get
g=6.7×10−11×7.4×1022(1.74×106)2
g=1.63m/s2
Thus the acceleration due to gravity, g, on the surface of the moon is 1.63 m/s2 .
Please note that the value of g on the moon is about one-sixth (1/6) of the value of g on the earth (the value of acceleration due to gravity on the earth being 9.8 m/s2)
MASS
Mass of an object is the measure of its inertia. Jitna jyada mass hoga, utna jyada inertia hoga. Earth, moon ya outer space, object ka mass har jagah same hota hai. The mass of a body is the quantity of matter contained in it. Mass scalar quantity hai jiska sirf magnitude hota hai, direction nahi hota. Body ka mass hamesha constant hota hai aur place to place change nahi hota hai. Mass ka SI unit kilogram (kg) hai. Kisi bhi body ka mass kabhi zero nahi ho sakta hai.
WEIGHT
Jis force se koi object earth ke centre ki taraf attract hota hai wahi force hi us object ka weight kehlata hai. The force with which an object is attracted towards the centre of the earth, is called the weight of the object.Now, Force =m×a
But in case of earth, a=g
∴F=m×g
But the force of attraction of earth on an object is called its weight (W).
∴W=mg
- Weight hamesha vertically downwards act karta hai isliye weight ka magnitude aur direction dono hota hai aur vo vector quantity hai.
- Weight place to place change hota hai aur object ke mass pr depend karta hai.
- Earth sare object ko attract karta hai ek force se aur ye force object ke mass aur acceleration due to gravity (g) pr depend karta hai.
- Kisi object pr earth ka force of attraction uska weight kehlata hai. Jise W se denote krte hai.
- Weight ka SI unit Newton (N) hai.
- Jab g zero hota hai to object ka weight bhi zero hota hai.
Weight of an Object on the Surface of Moon
Kisi object ka mass earth aur moon pr same hota hai. Lekin kisi object ka weight earth aur moon pr different hota hai. The weight of an object on the moon is the force with which the moon attracts that object. Moon ka mass earth ke mass se km hai isliye moon object pr less force of attraction exert karta hai.Let
Wm= The force with which the moon attracts the object
We= Force with which earth attracts the object
Wm=GMm.mR2m
Weight of the object on the moon is
WmWe=GMm.mR2m×R2eGMe×m
Or WmWe=MmMe×(ReRm)2
=Mm100Mm×(4RmRm)2
=16100≈16
Thus, the weight of an object on the moon is about one-sixth of its weight on the earth.
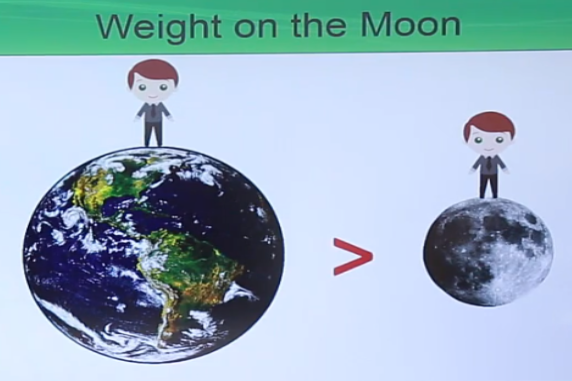
Weight of an object on the moon is less than that on the earth because the mass and the radius of the moon are less than that of earth due to which it exerts a lesser force of gravity.
POINT 3
Mass :
The mass of a body is the quantity of matter contained in it.
Weight :
The force with which an object is attracted towards the centre of the earth, is called the weight of the object.
EXAMPLE 9
Mass of an object is 10 kg. What is its weight on the earth?
Mass, m=10 Kg
Acceleration due to gravity, g=9.8ms−2
W=m×g
W=10kg×9.8ms−2=98N
Thus, the weight of the object is 98 N.
EXAMPLE 10
The weight of any person on the moon is about 1/6 times that on the earth. He can lift a mass of 15 kg on the earth. What will be the maximum mass, which can be lifted by the same force applied by the person on the moon ?
On earth Force applied by the man (F) on earth =m×g (m=mass)
On moon gm=g6
where gm= acceleration due to gravity on surface of moon.
Force applied to lift a mass of 15kg at the earth,
F=mg=15gN
∴ the mass lifted by same force on the moon,
m=Fgm=15gg6=90 kg
As Mass does not change at every place. It is concerned with quantity. So, 15 kg will be maximum mass which can be lifted by the same force applied by the person on the moon.
EXAMPLE 11
Calculate the average density of the earth in terms of g, G and R.
We know that, (g=GMR2) where M = Mass of the earth, R = Radius of the earth.
So, mass of the earth,M=gR2G
If the earth is considered as a shopere of radius R and of material of density ρ then
Mass of earth = volume of the earth×density
[∴volume of sphere=43πr3]
M=43πR3ρ
From Eq. (i), we get
∴ 43πR3ρ=gR2G
ρ=3g4πGR.
EXAMPLE 12
How does the force of attraction between the two bodies depend upon their masses and distance between them ? A student thought that two bricks tied together would fall faster than a single one under the action of gravity. Do you agree with his hypothesis or not ? Comment.
The force of attraction between two bodies of masses m1andm2 and separated by distance r is given by Newton's universal law of gravitation i.e., F=Gm1m2r2 where, G is the universal constant in nature.
This force is known as gravitational force. The gravitational force is directly proportional to the product of the masses of two bodies and inversely proportional to the square of the distance between them.
All bodies fall with the same acceleration due to gravity whatever their masses have.
i.e., g=GMR2
(where M = Mass of the earth, = Radius of the earth)
And from the equation it is clear that acceleration due to gravity (i.e., g) depends only on mass of the earth, the radius of the earth. So, two bricks tied together will not fall faster than a single bricks under the action of gravity. Hence, the hypothesis is not correct.
EXAMPLE 13
Two objects of masses m1andm2 having the same size are dropped simultaneously from heights h1andh2 respectively. Find out the ratio of time they would take in reaching the ground. Will this ratio remain the same if (i) one of the objects is hollow and the other one is solid and (ii) both of them are hollow, size remaining the same in each case. Give reason.
From second equation of motion, h=ut+12gt2 [for I object u=0]
So, h=12gt2
where, h = Displacement, u = Initial velocity, t = Time and g = Acceleration due to gravity
⇒ gt2=2h⇒t2=2hg
i.g., t=√2hg
∴Time taken by first object of mass,m1
t1=√2h1g [for II object u = 0]
Similarly, time taken by object of mass m2
t2√2h2g⇒t1t2=√h1h2
(i) Acceleration due to gravity is independent of the mass of the falling body. So, the ratio remains the same.
(ii) If bodies are hollow, then also ratio remains the same i.g.,t1:t2=√h1:√h2.
EXAMPLE 14
An object weight 10 N when measured on the surface of the earth. What would be its weight when measured on the surface of the moon?
We know,
weight of object on the moon =(1/6)× its weight on the earth
that is,
Wm=We6=106N.
=1.67N.
Thus, the weight of object on the surface of the moon would be 1.67 N.
THRUST AND PRESSURE
Thrust : Force exerted by an object perpendicular to the surface is called thrust.Kabhi apne socha hai ki camel desert me itne easily kaise run kr pate hain? Truck aur motorbus ka tyre wide kyu hota hai? Cutting tools ke sharp edges kyu hote hain? In sare questions ka answer karne ke liye hume ek phenomenon involved ko samjhna hoga. Jab hum loose sand pr khade hote hain, to force jo body ka weight hai vo ek area pr hamare feet ke area ke equal act karta hai. Thus, the effects of forces of the same magnitude on different areas are different. In the above cases, thrust is the same. But effects are different. Therefore the effect of thrust depends on the area on which it acts.
Pressure : Force exerted by any object per unit area is called pressure.
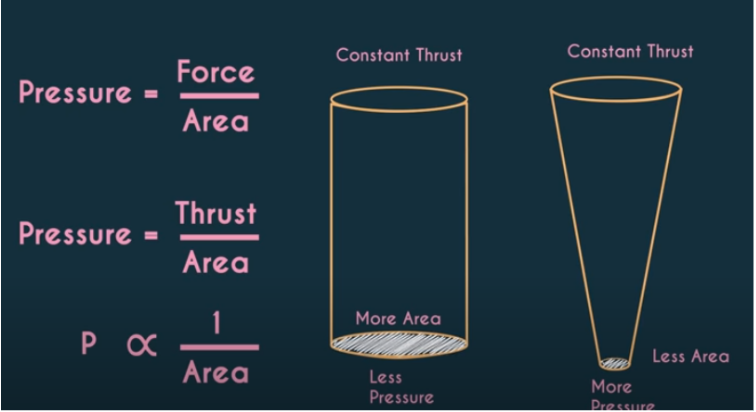
∴Pressure=ForceArea
Or, Pressure=ThrustArea
Or, P=FA ---(i)
Yaha pr, P pressure hai, F thrust or force hai aur A surface area of object hai.
SI unit of Pressure
Force ka unit newton (N) hai aur area ka unit square meter hai.
Therefore, by substituting the unit of force and are in equation (i) we get
P=N/m2 or Nm−2
So, pressure ka unit Nm−2 hai.
Blaise Pascal ke honor me pressure ka S.I. unit Pascal hai.
1 pascal 1 newton per square ke equal hota hai.
Or, 1 pascal =1Nm–2
Thrust and pressure in everyday life -
Pressure exerted by a brick :
Ager hum ek brick ko stretched position aur ek brick ko standing position me ground pr rakhe to standing brick pr jyada pressure exert hoga stretched brick se kyuki standing brick ka surface area km hai aur Pressure increase karta hai jab surface area decrease karta hai.
Knife with sharp edge cuts easily compare to one with blunt edge :
Sharp edge wale knife object pr jyada pressure exert karta hai kyuki unka surface area km hota hai. Isliye sharp knife se cut karna jyada easy hota hai blunt knife ke compare me.

Examples:
1. Jab hum ek pencil apne thumb aur index finger ke beech rakhte hain. Pencil ka tip index finger ko touch hote huye aur dusra end thumb ko touch hote huye. Phir dono side se equal force apply karte hain. Hum notice karte hain ki index finger me jyada depression hai aur thumb me km depression hai.
But jab hum dono side se equal force apply karte hain to Newton ke 3rd law ke according, pencil bhi fingers pr equal aur opposite force apply karega.
Depression jyada index finger pr hota hai kyunki pencil ka tip jo area pr force apply karta hai vo dusre end ke area se km hai. Area km hai to pressure jyada hoga aur depression bhi jyada hoga, area jyada hai toh pressure km lagega aur km depression hoga.
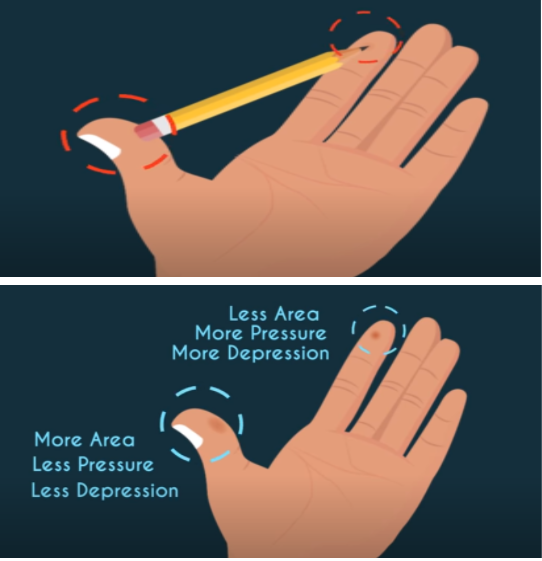
2. Jab hum loose sand pr khade hote hain to hum notice karte hai ki hmara feet deep sand me jata hai aur jab hum sand pr lie down hote hain to hum vaisa deep nahi jata hai. Ager force exerted dono cases me body ka weight hai to first case me depth kyu jata hota hai? Aisa hota hai kyuki feet ka area entire body ke area se km hota hai. Isliye feet pr jyada pressure lagta hai aur depth jyada hota hai. Entire body pr km pressure lagta hai aur depth km hota hai.

PRESSURE IN FLUIDS
Koi bhi solid object pressure exert karti hai apne weight ke karan. Vaise hi fluids ka bhi weight hota hai aur wo bhi pressure exert karta hai. Gas aur liquid dono ko fluids kahte hai. Fluids container ke inner wall pr sare direction me pressure exert karte hai jisme wo rakhe hote hai.BUOYANCY
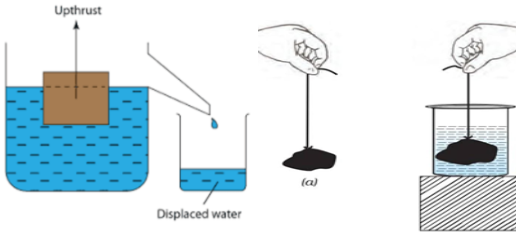
Kya aapko swimming pool me light feel hota hai? Kya aapne kabhi socha hai ki iron aur steel se bane ship kyu pani me dubate nahi hai jabki iron aur steel ka sheet pani me dub jata hai? In questions ka answer ke liye hume buoyancy ko samjhna hoga. Weight of an object is the force due to the gravitational attraction of the earth. Object force of buoyancy experience karte hain jab kisi bhi fluid me immerse hote hain. Buoyant force ka magnitude density of fluid pr depend karta hai. The upward force exerted by the water on the object is known as upthrust or buoyancy force.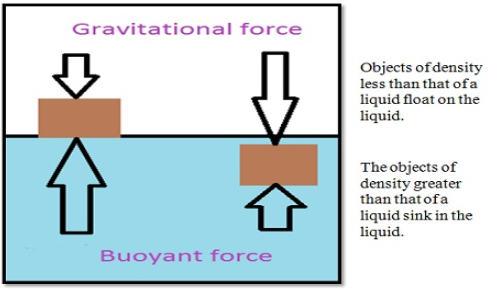
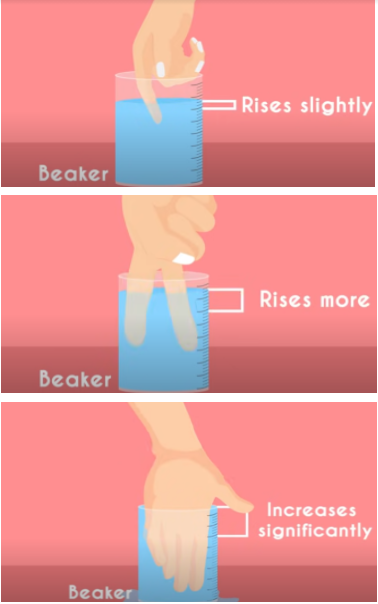
Niche diye gaye images me aap dekhenge jab hum ek finger pani me dalenge to pani ka level slightly rise hoga, jab do finger dalenge to pani ka level thoda aur rise hoga aur jab pura palm dalenge toh pani ka level significantly increase ho jaega.
POINT 4
Thrust :
Force exerted by an object perpendicular to the surface is called thrust.
Pressure :
Force exerted by any object per unit area is called pressure.
Buoyancy :
The upward force exerted by fluids (liquid and gas) on objects when they are immersed in them is called buoyant force and also upthrust and the phenomenon is called buoyancy.
EXAMPLE 15
A block of wood is kept on a table top. The mass of wooden block is 5 kg and its dimensions are 40cm×20cm×10cm. Find the pressure exerted by the wooden block on the table top if it is made to lie on the table top with its siders of dimensions (a)20cm×10cmand(b)40cm×20cm
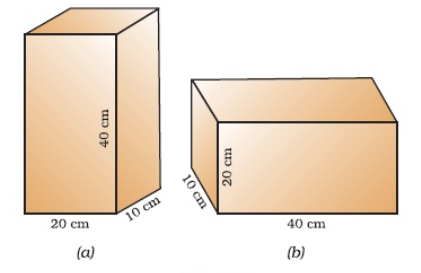
The mass of the wooden block =5 kg
the dimensions =40cm×20cm×10cm
Here, the weight of the wooden block applies a thrust on the table top .
i.e. Thrust =F=m×g
=5kg×9.8ms−2
=49N
Area of side = length× breadth
=20cm×10cm
=200cm2=0.02m2
From Eq. (20)
Pressure =490.02m2
=2450Nm−2
When the block lies on its side of dimensions 40cm×20cm, it exerts the same thrust
Area = length × breadth
=40cm×20cm
=800cm2=0.08m2
From Eq. (20),
pressure =490.08m2
=612.5Nm−2
The pressure exerted by the side 20cm×10cm is 2450Nm2 and by th side 40cm×20cm is 612.5Nm−2.
EXAMPLE 16
(i) A cube of side 5 cm is immersed in water and then in a saturated salt solution. In which case will it experience a greater buoyant force. If each side of the cube is reduced to 4 cm and then immersed in water, what will be the effect on the buoyant force experienced by the cube as compared to the first case for water. Give reason for each case.
A ball weighing 4 kg of density 4000 kgm−3 is completely immersed in water of density 103Kgm−3. Find the force of buoyancy on it. (Given, g = 10 ms−2)
(i) Buoyant force, F=V ρg
(where, ρ = Density of water, V = Volume of water displaced by body)
Buoyant force depends upon volume. So, in a saturated solution, the cube will experience a greater buoyant force.
If each side of the cube is reduced to 4 cm, then the volume of the cube becomes less. As buoyant force is directly proportional to the volume. So, buoyant force will be less than as compared to the first case for water.
(ii) The magnitude of the buoyant force given by F=Vρg
where V = Volume of body immersed in water or volume of water displaced, ρ = Density of liquid. [∴Given, mass of a ball=4kg,density=4000kgm−3]
∴ Volume of solid=MassDensity
=44000=11000m3
Buoyancy, F=Vρg
=11000×1000×10=10N.
ARCHIMEDES’S PRINCIPLE
Archimedes’ Principle states that “When a body is immersed fully or partially in a fluid, it experiences an upward force that is equal to the weight of the fluid displaced by it.” Koi chiz jab pani ke ander daali jati hai toh uska weight km lgta hai lekin jab us chiz ko pani ke bahar nikal lete hain tb uska weight jyada lagta hai. Jab ek body pani me puri tarah se dubi hai tb pani ke karan wo ek upward force feel karti hai. Koi chiz ko jab hum pani me duba dete hai to pani ka level uper aa jata hai. Ye bhadhe hue pani ko water displaced kahte hain.

Upward force is equal to the weight of the water displaced by the body. Archimedes’ Principle dono cases me kaam krta hai, jab koi body pani me puri tarah se duba hota hai ya uska kuch ek bhaag pani ke ander hota hai. Archimedes’s Principle kisi bhi liquid or gas or koi bhi fluid ke liye apply kiya ja sakta hai.
Example: Jab hum ek plastic ball ko pani me dubote hai to upward force ko feel kar pate hai aur jaise hi hum haath hata dete hai to ball upward force ke karan upr aa jati hai. Pani ball ke upr ek upward force deti hai aur is upward force ko upthrust ya buoyant force kahte hain.
How To Measure the Upward Force?
Upward Force= Loss in Weight
Loss in weight= Weight in air- Weight in water
Ager hum ek body ko kisi bhi liquid me dalenge (no matter fully or partially), the body upward force experience karta hai aur wo upward force us displaced liquid ke weight ke equal hota hai. Isi reason se body Upthrust experience krti hai displaced liquid ke weight ke equal hoti hai.
Ager displaced liquid ka weight body ke weight se km hai toh body dub jaega.
Relation Between Upward Force and Volume of the Liquid Displaced
Upward force= weight of liquid displaced
w=m×g
m=V×d
Upward force=Vdg
Yahan V volume of displaced liquid hai, d liquid ka density hai.
Therefore, Upward force =VLdLg
VL vol. of liquid hai aur dL density of liquid hai.
Archimedes’s Principle se hum samjh sakte hain ki chhota steel coin pani me kyu dub jata hai lekin ek bahut bara steel jahaj pani me float kar sakta hai jabki dono same material, steel se bane hain.

Experiment:
Ek ball ke ander hum kuch coins daal denge jisse ball bhari ho jaye aur pani me dub jaye. Is ball ko pani me dubne se phle spring balance se iska weight measure kr lenge. Suppose, spring balance me ball ka weight 500g dikhata hai.
Weight of the ball = 500gf (Is weight ko hum weight in air ya real weight kahte hain kyon ki ye ball ka actual weight hai).
Ab hum is ball ko pani me dubo denge. Tb hum dekhte hain ki pani me ball ka weight km ho jata hai, 300gf.
Jab koi chiz pani ke ander hoti hai to uske weight ko hm apparent weight (weight in water) kehte hai. Apparent Weight ka mtlb hai jo weight hume feel hota hai aur ye actual weight nahi hai.
Loss in weight= real weight- apparent weight
=500gf−300gf
=200gf.
Ball ka loss in weight upward force ke karan hota hai.
Upward Force =200gf.

OMR (One Minute Revision)
- *Archimedes Principle sirf liquid ke liye hi nahi, gases ke lie v apply hoti hai.
* Upthrust is the force jo body pr lagta hai, jab bhi koi body liquid mein duboya hua hota hai.
* If the weight of the water displaced is less than the weight of the object, the object will sink.
* Jab body liquid me duboya hua hota hai to uska weight km lagta hai because of upthrust. That loss in weight is equal to the upthrust on the body.
* Upward Force= Weight of the fluid displaced.
* Loss in weight= Real Weight- Apparent Weight
* Upward Force= loss in weight
* Upward force =VLdLg
APPLICATIONS OF ARCHIMEDES’ PRINCIPLE
RELATIVE DENSITY
The density of a substance is defined as mass of a unit volume. The unit of density is kilogram per metre cube (kgm–3). Kisi substance ka density specified conditions me same rehta hai. Therefore the density of a substance is one of its characteristic properties. It is different for different substances.Density=Mass of the substanceVolume of the substance
D=MV
Relative density of a substance is defined as the ratio between the density of the substance to the density of water at 40C. Relative density is also known as specific gravity. It tells how many times a substance is heavier than water.
Relative density (R.D) of a substance ka hum calculate kar sakte hain relative density of substance ko relative density of water se divide karke. Relative density similar quantities ka ratio hota hai isliye uska koi unit nahi hota hai.
Relative Density of substance=Density of the substanceDensity of water
POINT 5
Archimedes principle :
whenever an object is immersed in a liquid (fully or partially), the liquid exerts an upward force upon the object. The amount of that force is equivalent to the weight of the liquid displaced by the object.
Density :
The density (ρ) of a substance is defined as mass of a unit volume.
Relative Density :
The relative density of a substance is the ratio of its density to that of water.
EXAMPLE 17
When an aluminium object is immersed in water it displaces 5 kg of water. How much is the buoyant force acting on the aluminium object in newtons? (g=10m/s2)
According to Archimedes Principle, the buoyant force acting on this aluminium object will be equal to the weight of water displaced by this aluminium object. So, all that we have to do is to find the weight of water displaced in 'newtons'. That will give us the buoyant force. We know that: weight W=m×g
Here, Mass of water m=5 kg
and Acceleration due to gravity g=10m/s2
Now, putting these values of m and g in the above formula, we get : Weight of water W=5×10N
=50N
Now, since the weight of water displaced by the aluminium object is 50N, therefore, the buoyant force acting will also be 50 newtons.
EXAMPLE 18
The mass of 2m3 of steel is 15600 kg. Calculate the density of steel in SI untis.
We know that: Density =MassVolume
=15600kg2m3
=7800kg/m3
Thus, the density of steel in SI units is = 7800kg/m3.
EXAMPLE 19
A ball is thrown vertically upwards with a velocity of 49 m/s. Calculate
(i) the maximum height to which it rises,
(ii) the total time it takes to return to the surface of the earth.
Accrding to the equation of motion under gravity
v2−u2=2gs
where
u= intial velocity of the ball
v= final velocity of the ball
s= Height achieved by the ball
g= Acceleration due to gravity
At maximum height , final velocity of the ball is zero ,i.e., v=0
u=49 m/s
During upward , g=-9.8ms−2
let h be the maximum height attained by the ball
Hence ,
0−492=2×9.8×h
⇒h=492/(2×9.8)
⇒h=2401/19.6=1225.5
Let t be the times taken by the ball to reach the height 122.5 m. then according to the equation of motion :
v=u+gt
We get
0=49+t×)−9.8)
9.8t=49
t=49/9.8=5s
Also ,
time of ascent = Time of descent
therefore , total time taken by the ball to return =5+5=10s