TRIANGLES for Class 9 MATHS
Introduction
So bacho, jaisa ki hum previous classes me triangles ke bare padhte aaye hai. Us knowledge ko next level par le jate huye is chapter me hum triangles ke kuch special properties ko detail me pdhenge. Ab tak humne sikha hai, a triangle can be denoted by △ABC and it is a closed figure made up of 3 sides AB,BC and CA and have 3 vertices A,B and C and have 3 angles ∠A,∠B and ∠C. So basically in this chapter, you will study in details about the congruence of triangles, rules of congruence, some more properties of triangles and inequalities in a triangle.
Concept of Congruence
Two figures are said to be congruent if they have the same shapes and sizes. For example aapne aksar dhyan diya hoga two copies of your photographs are identical jiske shape and size same hote hai. Similarly, two bangles of the same size, two ATM cards issued by the same bank are identical. Thik waise hi agar hum same radius wale two circles ki baat karte hai ya hum baat karte hai same side wale two squares ki. Hum or kuch nahi two identical figures ki baat kar rahe hote hai jinhe congruent figures kha jata hai. So basically congruent means equal in all respects or figures whose shapes and sizes are both the same.
Congruence of a Triangle
Two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle. It is called congruent triangles, in which all corresponding parts are equal and we write in short ‘CPCT’ for corresponding parts of congruent triangles.
Congruent Figures
Let us consider two congruent triangles △ABC and △PQR . Which is given below lakin we have to show it mathematically. 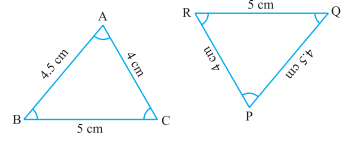
Here we can see that ∠A=∠P , ∠B=∠Q and ∠C=∠R so it is written as A↔P,B↔Q, C↔R .
Similarly side AB= side PQ , side BC= side QR and side AC= side PQ can be represented as AB↔PQ , BC↔QR , AC↔PR .
So, we can see that the corresponding sides and angles of both the triangles are the same which shows that △ABC and △PQR are congruent figures .
If △ABC is congruent to △PQR then we will write it as △PQR≅△ABC.
Note: Order of letter A, B, C is important; it should match with the angle or side of the triangle which is congruent to the given triangle.
Criteria for Congruence of Triangles
Now we know two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle lakin two triangle ko congruent prove karne ke liye we have different ways. Like if we want to prove two bangles are the same then we can measure length of diameter and compare, or we can measure length of circumference, or we can put one on another. Similarly two triangles ko bhi congruent prove karne ke liye hum different theorems or axioms ka use karte hai. Is pure chapter me basically hum in methods ki baat karenge or unse related problems ko solve bhi karenge.
Axiom 7.1
SAS congruence rule : Two triangles are congruent if two sides and the included angle of one triangle are equal to the sides and the included angle of the other triangle.
Note : SAS stands for side angle side.
It means if any two sides of two triangles and angle between them are equal then both triangles are congruent. Hum ise figure ke help se samajh sakte hai.
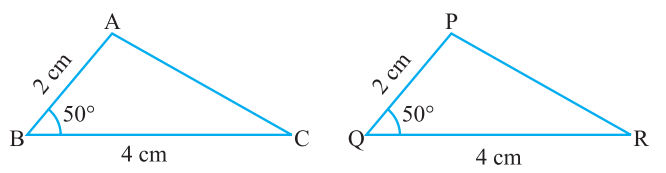
Here we have two triangles, △ABC and △PQR . Where AB=PQ and BC=QR as well as ∠B=∠Q .
So, according to the axiom 7.1 we can say that
△ABC≅△PQR .
Example 1
In the given figure, OA = OB and OC = OD . Show that:
ΔAOC≅ΔBOD

In ΔOACandΔOBD, we have
OA = OB (given),
OC = OD (given)
and ∠AOC=∠BOD
(vertically opposite angles).
∴ ΔOAC≅ΔOBD (by SAS-criteria). Proved
Example 2
If D is the midpoint of the hypotenuse AC of a right-angled ΔABC, prove that BD=12AC.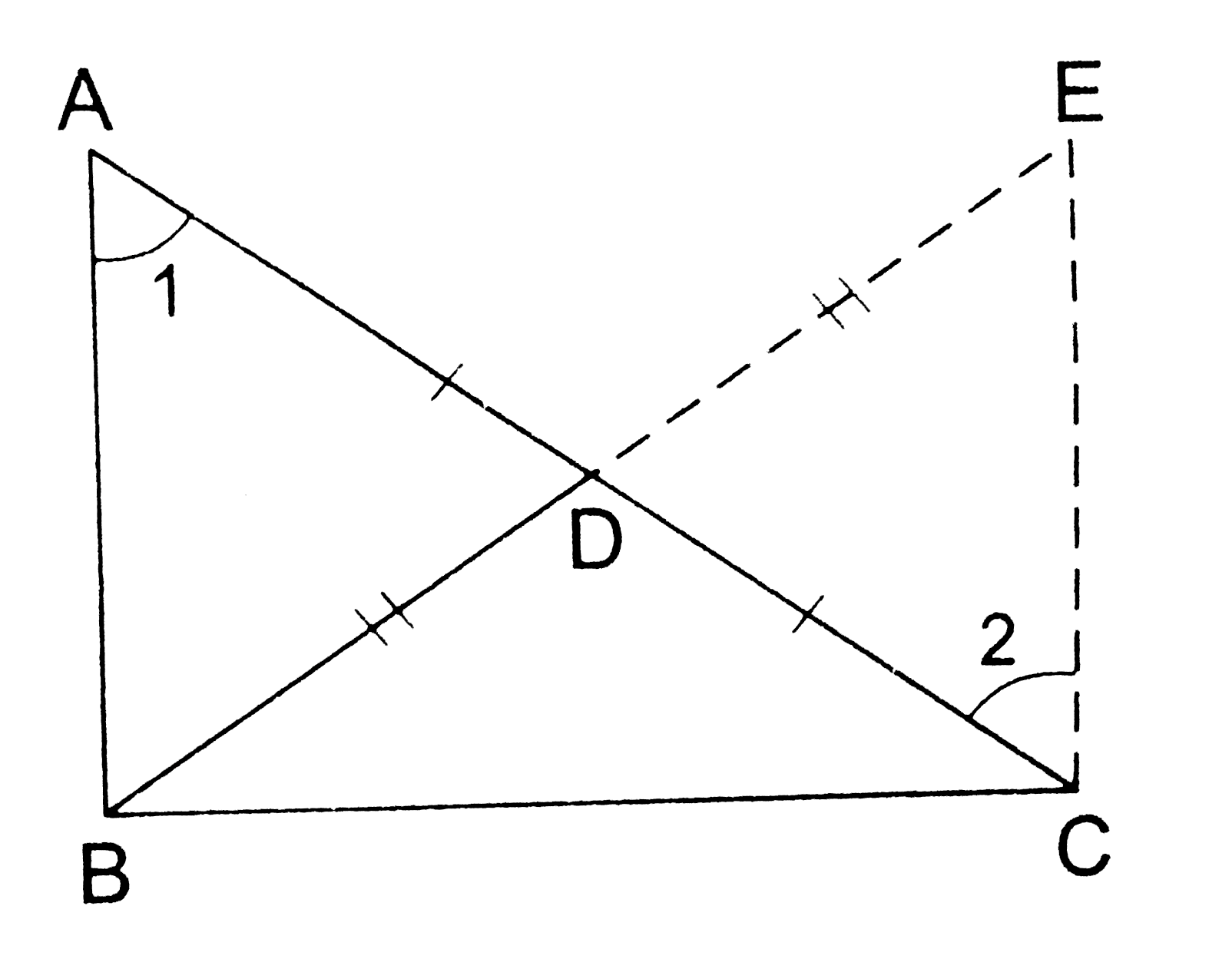
Given a ΔABC in which ∠B=90∘ and D is the midpoint of AC.
To Prove BD=12AC.
CONSTRUCTION : Produce BD to E such that BD = DE and join EC.
PROOF : In ΔADBandΔCDE, we have
AD=CD (given)
BD=ED (by construction)
and ∠ADB=∠CDB (vertically opposit angles).
∴ ΔADB≅ΔCDE (SAS-criteria) .
So, AB=ECand∠1=∠2 (C.P.C.T) .
But, ∠1and∠2 are alternate interior angles .
∴ CE||BA.
Now jaisa ki hum jante hai, if CE||BA and BC is the transversal,
then ∠ABC+∠BCE=180∘ [Co-interior angles]
⇒ 90∘+∠BCE=180∘ [because∠ABC=90∘]
⇒ ∠BCE=90∘
Now, inΔABCandΔECB, we have
BC=CB (common),
AB=EC (proved)
and∠CBA=∠BCE (each equal to 90∘).
∴ ΔABC≅ΔECB (SAS-criteria).
∴ AC=EB
We can also write EB=AC⇒12EB=12AC
Here 12EB=BD
So, hum ye keh sakte hai BD=12AC.
Hence, BD=12AC.
Theorem 7.1
ASA congruence rule : Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of another triangle.
Let us consider two triangles, △ABC and △DEF such that
∠B=∠E , ∠C=∠F.
and BC=EF 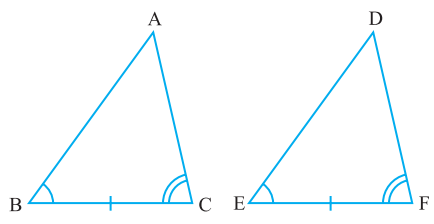
Here we need to prove △ABC≅△DEF.
For proving congruence we have 3 cases :
Case 1 : Let AB = DE
So now we have
AB=DE (assumed)
∠B=∠E (Given)
BC=EF (Given)
So, △ABC≅△DEF (By SAS rule) .
Case 2: AB > DE
So, we can take a point P on AB such that PB=DE. Now consider △PBC and △DEF
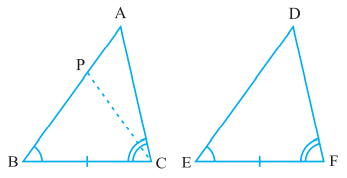
Here, PB=DE (By construction)
∠B=∠E (Given)
BC=EF (Given)
So, △PBC≅△DEF (By SAS rule)
Jaisa ki hum jante hai if two triangles are congruent then unke corresponding parts bhi equal hote hai.
So, ∠PCB=∠DFE
But, we are given that ∠ACB=∠DFE
So, ∠ACB=∠PCB
Lakin aisa kewal tab hi possible hai jab point P coincides with vertex A.
∴BA=ED
So, △ABC≅△DEF (By SAS rule) .
Case 3 : If AB < DE
We can choose a point M on DE such that ME=AB and
repeating the arguments as given in Case (ii), we can conclude that AB=DE and so,
ΔABC≅ΔDEF.
Therefore we conclude that if two angles and a side between them are equal then both triangles are congruent.
Note :
Example 3
In the given figure, AB = AC and ∠B=∠C.
Prove that ΔABD≅ΔACE.
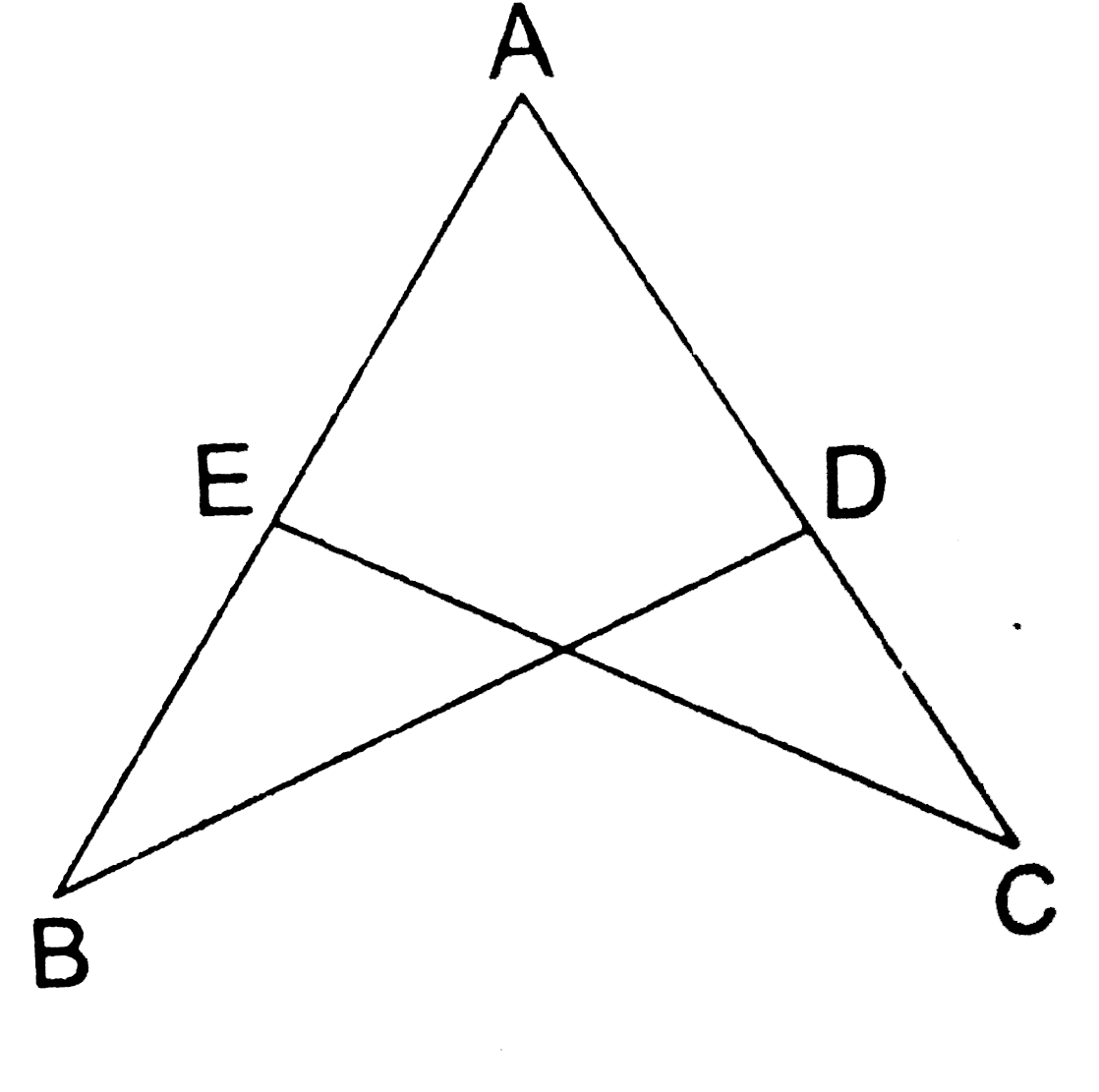
In ΔABDandΔACE, we have
AB=AC (given)
∠ABD=∠ACE [∵∠B=∠C (given)]
∠BAD=∠CAE [common]
∴ ΔABD≅ΔACE [ASA-criteria].
Example 4
In the adjoining figure, AD is a median of ΔABC. If BL and CM are drawn perpendiculars on AD and AD produced , prove that BL = CM.
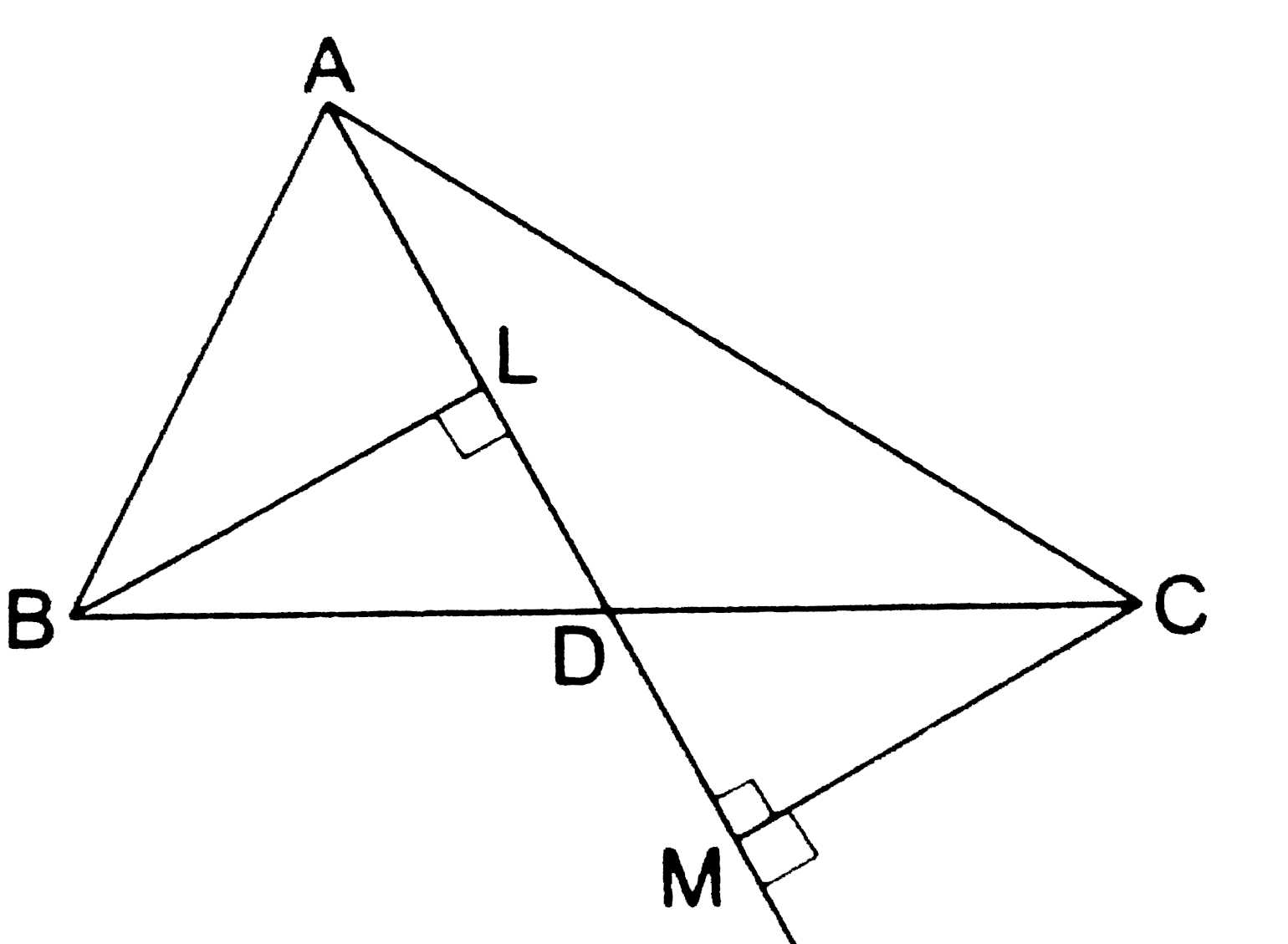
In right triangles ΔBLD and ΔCMD, we have
BD=CD [∵D is the midpoint of BC]
∠BLD=∠CMD [each equal to 90∘]
∠BDL=∠CDM [vertically opposit angles]
∴ ΔBLD≅ΔCMD [AAS-criteria] .
Hence, BL=CM [C.P.C.T]
Some Properties of a Triangle
We know a triangle in which two sides are equal is called an isosceles triangle. You may observe that in each such triangle, the angles opposite to the equal sides are equal. Ise hum theorem ki help se solve karenge.
Theorem 7.2
Angles opposite to equal sides of an isosceles triangle are equal.
Let we have isosceles triangle ABC in which AB=AC. 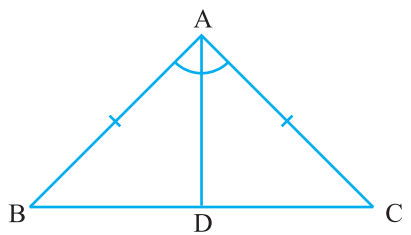
We need to prove that ∠B=∠C.
Draw the bisector of ∠A and let D be the point of intersection of this bisector of ∠A and BC.
Ab yha hum dekh sakte hai, in △BAD and △CAD,
AB=AC (Given)
∠BAD=∠CAD (By construction)
and AD=AD (Common)
So, ΔBAD≅ΔCAD (By SAS rule)
So, ∠ABD=∠ACD, since they are corresponding angles of congruent triangles.
∴∠B=∠C, Proved.
Example 5
ΔABC is an isosceles triangle with AB = AC. Where side BA is produced to D such that AB = AD. Prove that ∠BCD is a right angle.
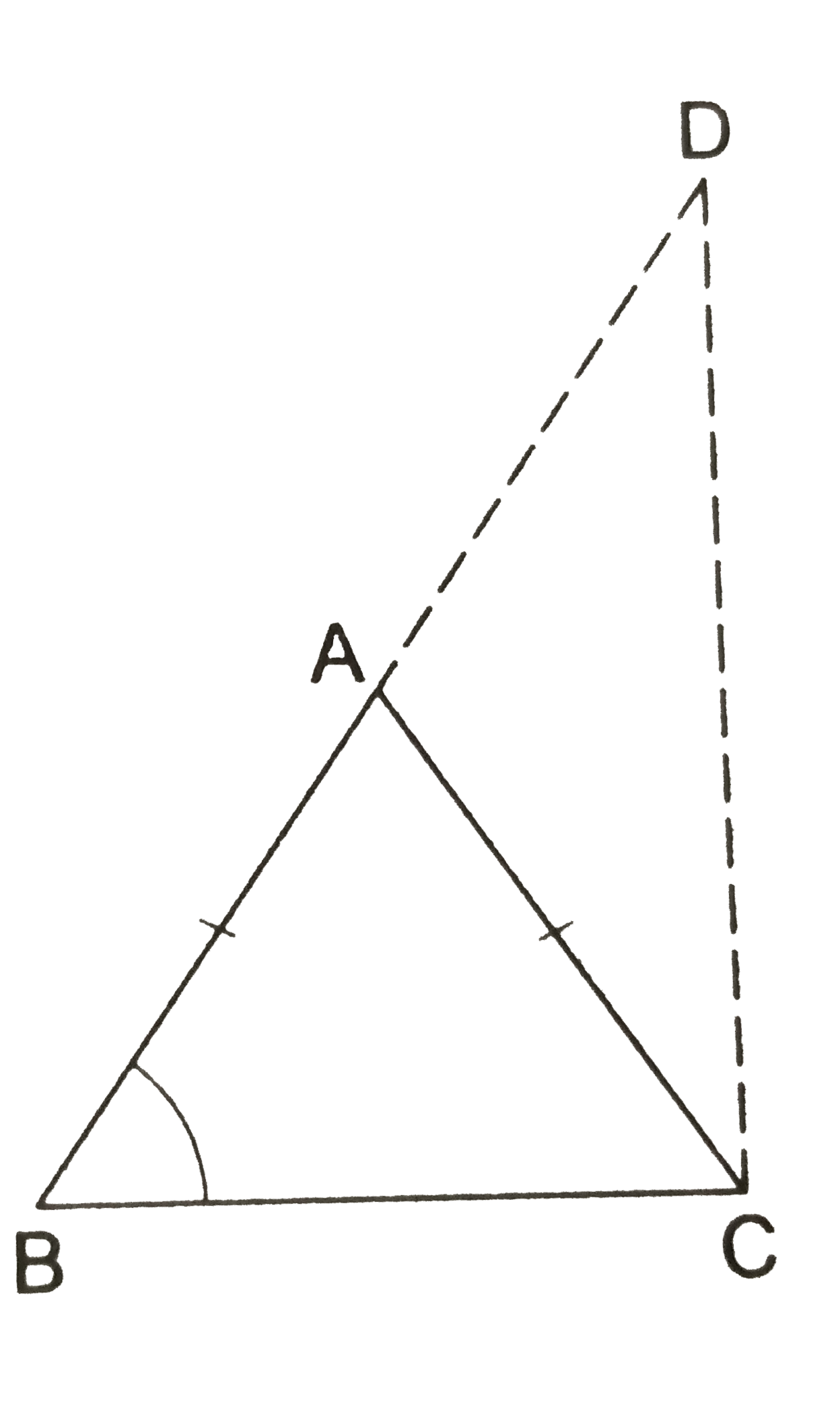
Given a ΔABC in which AB=AC and BA is produced to D such that AB=AD.
To prove ∠BCD=90∘
CONSTRUCTIONS : Produced BA to D such that BA = AD and join DC .
PROOF : AB=ACandAB=AD⇒AD=AC.
Now, AB=AC⇒∠ABC=∠ACB (theorem 7.2),
since AD=AC⇒∠ADC=∠ACD (theorem 7.2),
∴ ∠ABC+∠ADC=∠ACB+∠ACD.
⇒ ∠ABC+∠ADC=∠BCD [∵∠ACB+∠ACD=∠BCD]
⇒ ∠ABC+∠ADC+∠BCD=2∠BCD [adding ∠BCD on both sides]
⇒ 2∠BCD=180∘ [∵ sum of the angles of ΔABD is 180∘]
⇒ ∠BCD=90∘.
Hence, ∠BCD is a right angle.
Theorem 7.3
The sides opposite to equal angles of a triangle are equal.
Let we have triangle ABC in which ∠B=∠C. We need to prove that AB=AC.
Draw the bisector of ∠A and let D be the point of intersection of this bisector of ∠A and BC.
Now we have two triangles, in △BAD and △CAD,
∠B=∠C (Given)
∠BAD=∠CAD (By construction)
and AD=AD (Common)
So, ΔBAD≅ΔCAD (By AAS rule)
∴AB=AC since they are corresponding sides of congruent triangles.
∴AB=AC, Proved.
Example 6
The bisectors of ∠Band∠C of an isosceles ΔABC with AB=AC intersect each other at a point O. Show that the exterior angle adjacent to ∠ABC is equal to ∠BOC.
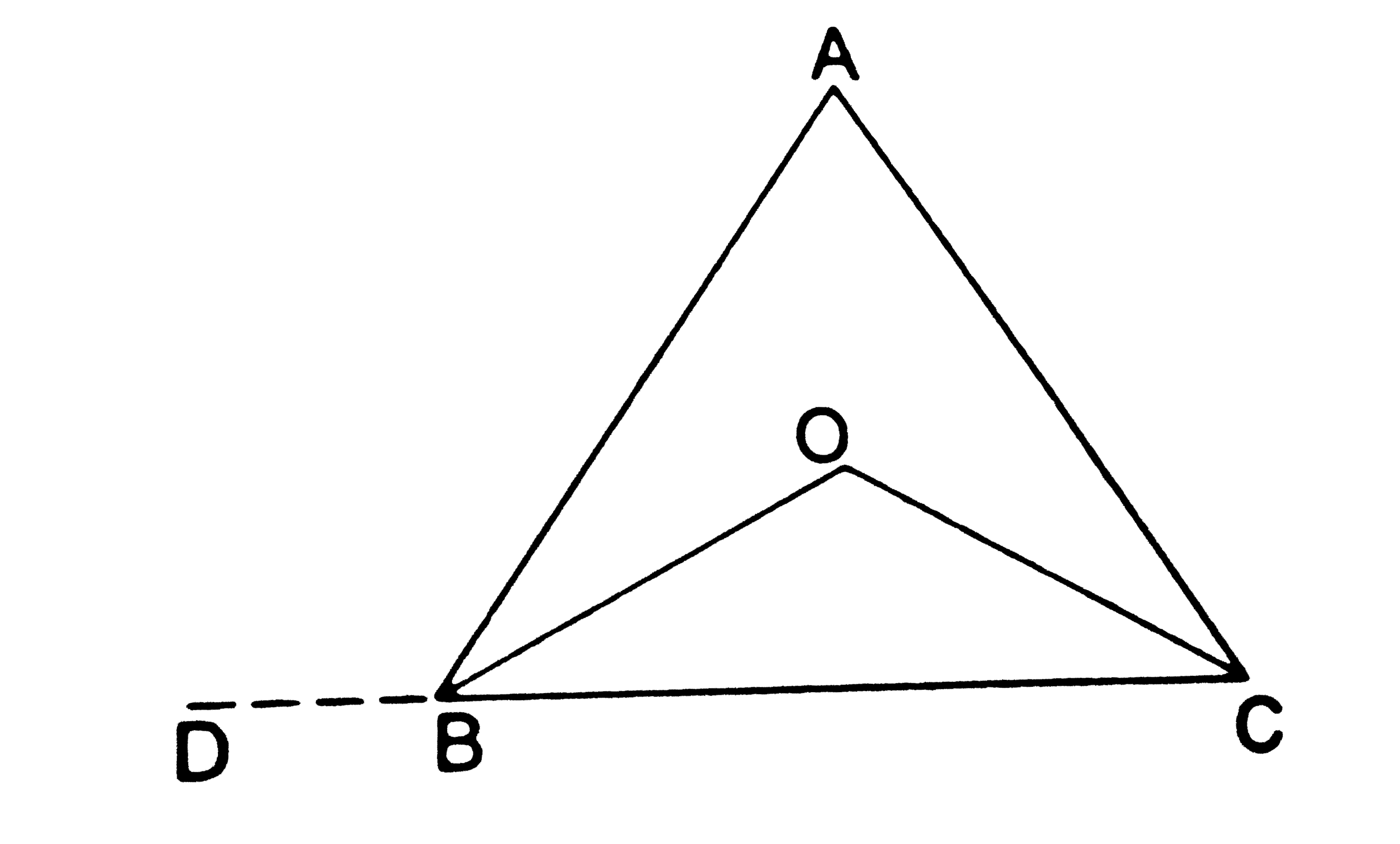
AB=AC⇒∠ACB=∠ABC (theorem 7.2)
⇒12∠ACB=12∠ABC
⇒∠OCB=∠OBC.
In ΔBOC, we have
∠OBC+∠OCB+∠BOC=180∘
⇒ 2∠OBC+∠BOC=180∘
⇒ ∠ABC+∠BOC=180∘
⇒ 180∘−∠DBA+∠BOC=180∘⇒∠DBA=∠BOC.
Hence proved
Theorem 7.4
SSS congruence rule : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
Given AB=DE,AC=DFandBC=EF.
To Prove, △ABC≅△DEF. 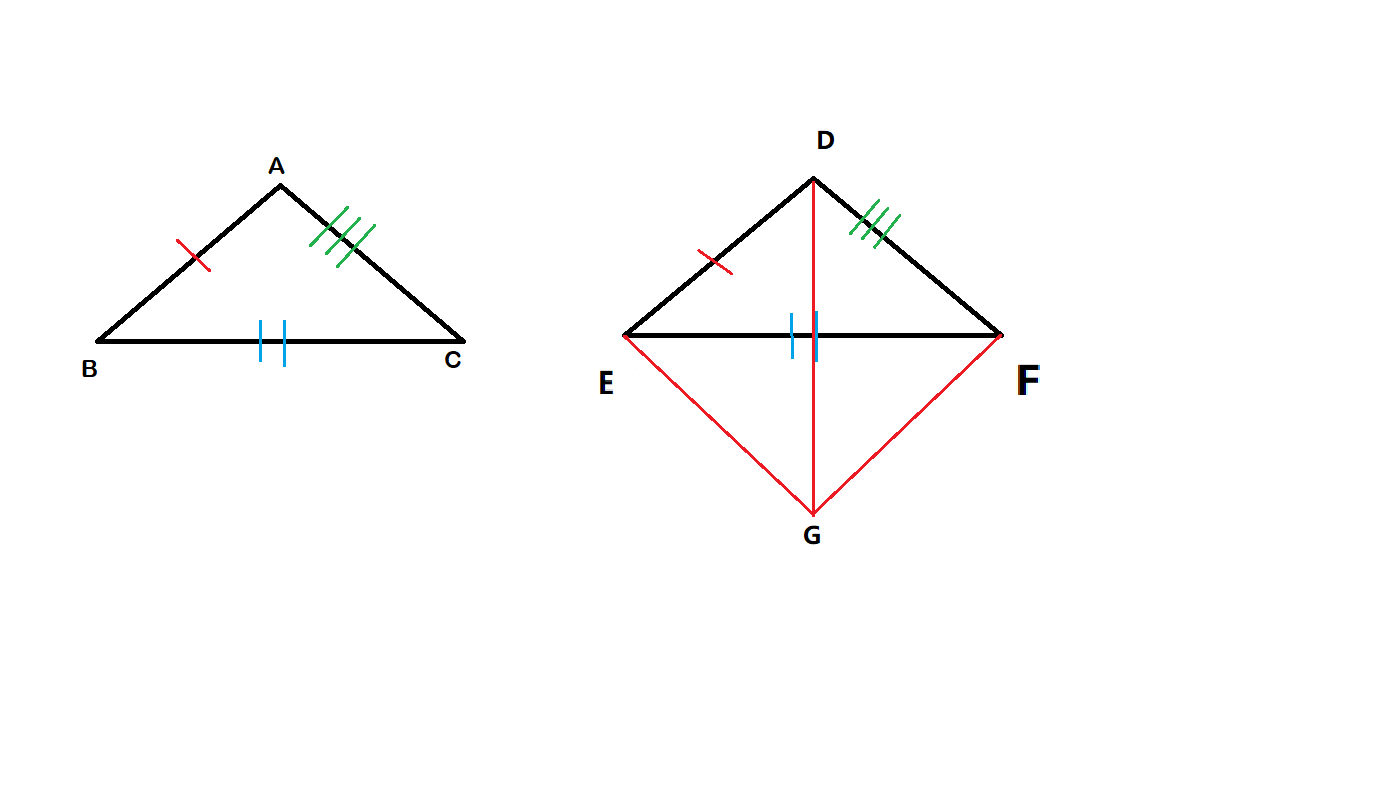
CONSTRUCTION : Draw EG and FG such that , ∠FEG=∠ABC and join DG.
In △ABC and △GEF
∠ABC=∠FEG (by construction )
∠ACB=∠EFG (by construction)
and BC=EF (given)
∴△ABC≅△GEF (by A.S.A criteria)
So, ∠A=∠G ........(i) [C.P.C.T]
AB=GE.........(ii) [C.P.C.T]
AC=GF ........(iii)[C.P.C.T]
But, AB=DE (given)
∴DE=GE (using ii)
Similarly AC=DF (given )
∴DF=GF (using iii)
By the property of isoceleus triangle
Since DE=GE⇒∠EDG=∠EGD.........(v)
Similarly, DF=GF⇒∠FDG=∠FGD.........(vi)
Adding (v) and (vi) we have,
∠EDG+∠FDG=∠EGD+∠FGD
⇒∠D=∠G
As we proved earlier ∠A=∠G .
So we can write ∠D=∠A ,
Now, in △ABC and △DEF,
∠D=∠A(proved )
AB=DE(given)
and AC=DF (given )
∴△ABC≅△DEF Proved
Example 7
In the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
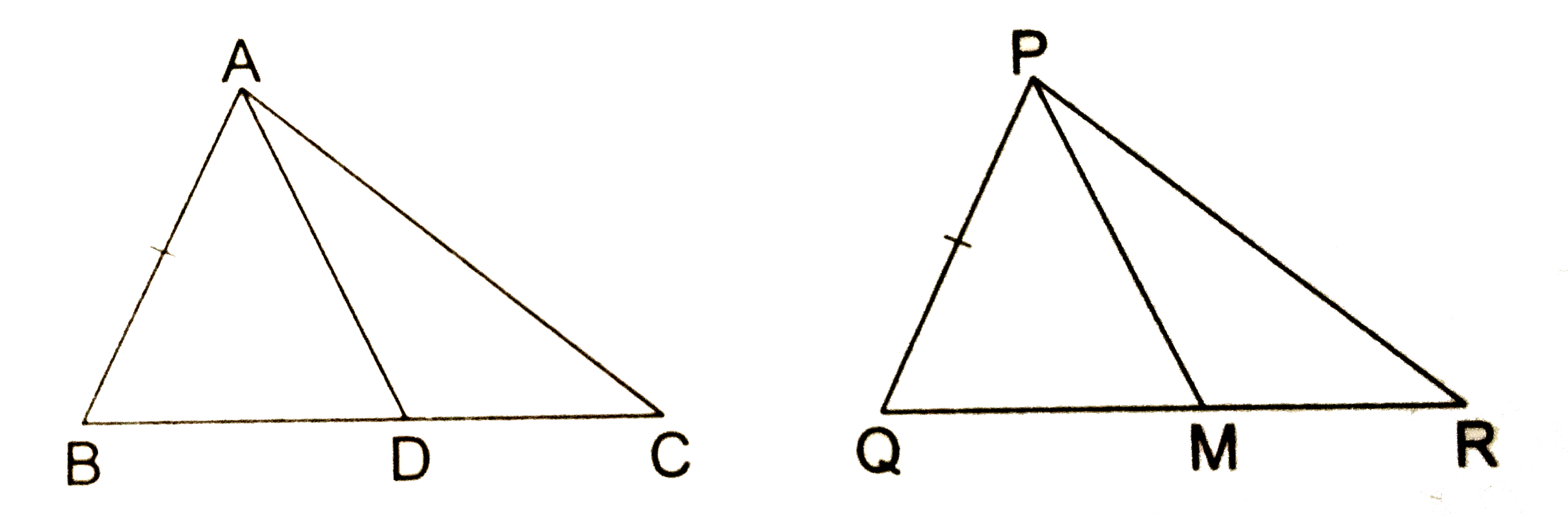
Given ΔABC and ΔPQR in which AB=PQ , BC=QR and median AD of ΔABC=median PM of ΔPQR .
To prove ΔABC≅ΔPQR.
PROOF : In ΔABDandΔPQM, we have
AB=PQ (given)
BD=QM [becauseBC=QR⇒12BC=12QR⇒BD=QM]
median AD = median PM (given)
∴ ΔABD≅ΔPQR (SSS-criteria).
∴ ∠ABD=∠PQM (C.P.C.T.),
⇒ ∠ABC=∠PQR.
Now, in ΔABCandΔPQR, we have
AB=PQ (given)
∠ABC=∠PQR (proved above)
BC=QR (given).
∴ ΔABC≅ΔPQR (SAS-criteria).
Theorem 7.5
RHS congruence rule : If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Let we have △ABC and △PQR right-angled at B and Q respectively such that
AB=PQ (equal sides) ........(1)
and AC=PR (equal hypotenuse) ........(2)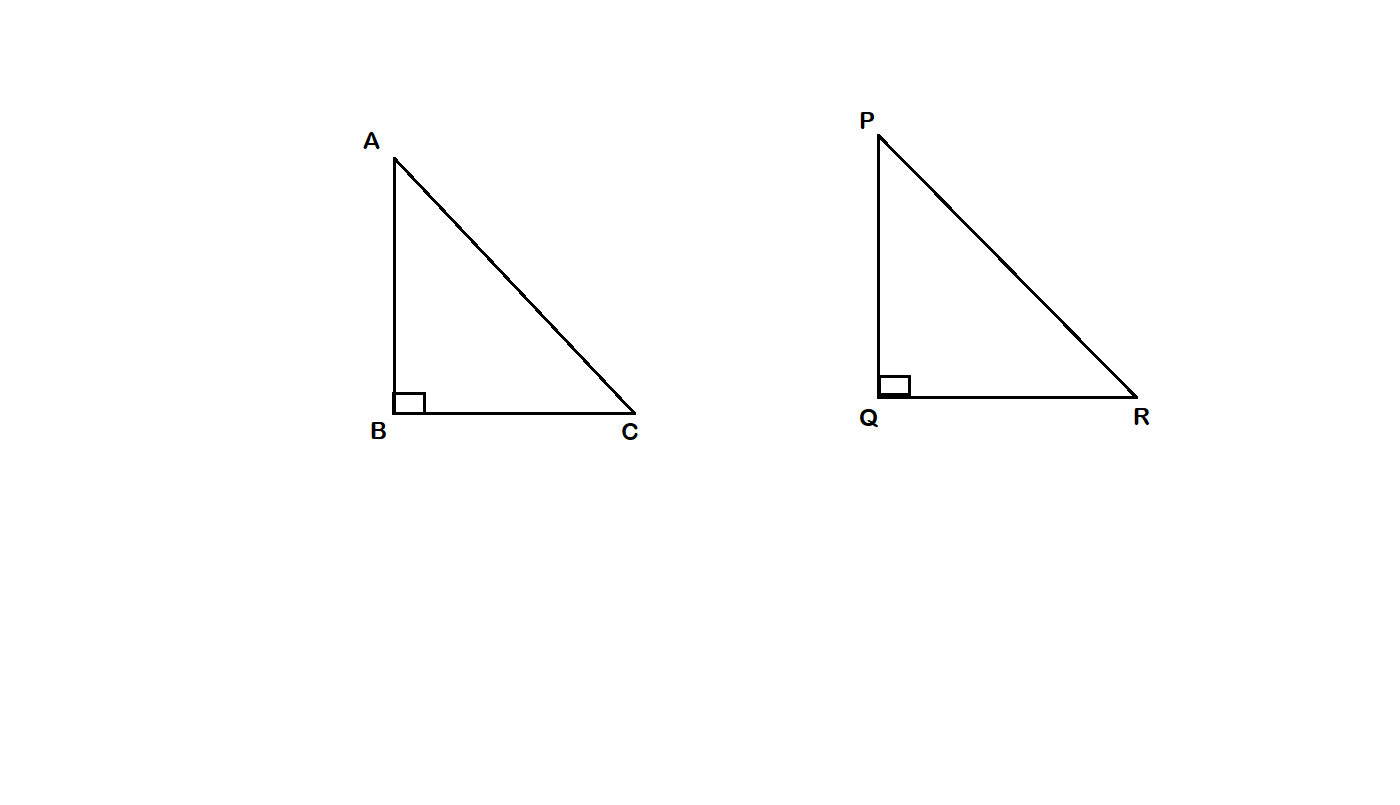
Since ABCandPQR is a right-angle triangle,
∴AB2+BC2=AC2 and PQ2+QR2=PR2
BC2=AC2−AB2............(3)
But AC=PR and AB=PQ.
So, AC2−AB2=PR2−PQ2=QR2........(4)
∴BC2=QR2 (from (3) and (4))
⇒BC=QR.........(5)
∴ from (1), (2) and (5) by SSS we have
△ABC≅△PQR.
Example 8
In the given figure, BA⊥ACandDE⊥DF such that AB = DE and BF = EC. Show that ΔABC≅ΔDEF.
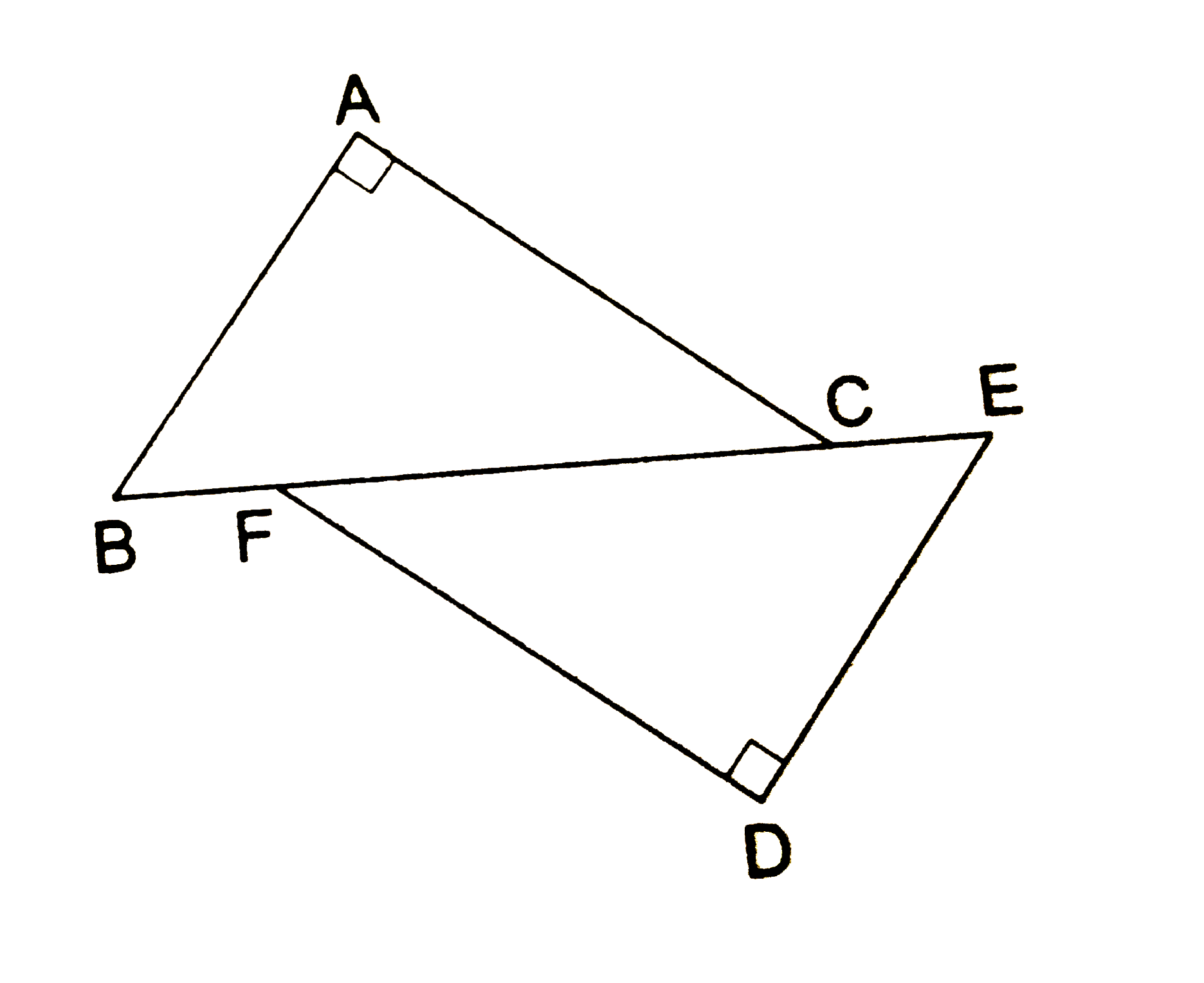
Given, BA⊥ACandDE⊥DF such that AB=DEandBF=EC.
To Prove ΔABC≅ΔDEF.
PROOF : EC=BF⇒BE−EC=BE−BF
⇒BC=EF. ...(i)
In ΔABCandΔDEF, we have
AB=DE (given)
∠BAC=∠EDF=90∘
hyp. BC = hyp. EF (from (i))
∴ ΔABC≅ΔDEF [by RHS-criteria].
Inequalities in a Triangle
Like inequality in numbers 3>2 or 5<9 we have Inequality in triangle in angles or sides, i.e. ∠A>∠B or AB>CD
Theorem 7.6
If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater).
Let ABC be triangle such that AB>AC
Here we have to prove ∠C>∠B.
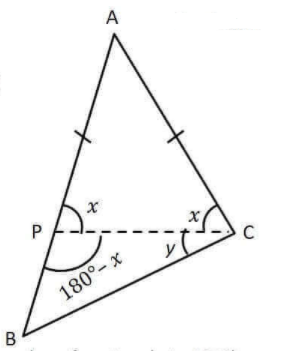
Now take P on AC such that AP=AC.
Now from theorem 7.2 we have,
∠ACP=∠APC=x and let ∠PCB=y
Therefore ∠BPC=180∘−x .
So in triangle BPC sum of interior angle =180∘
∠BPC+∠PBC+∠PCB=180∘
Or, 180∘−x+∠PBC+y=180∘
∴∠PBC=x−y
∴∠B=x−y
Also we have ∠C=x+y
therefore, ∠C>∠B .
Example 9
In a right-angled triangle, prove that the hypotenuse is the longest side.
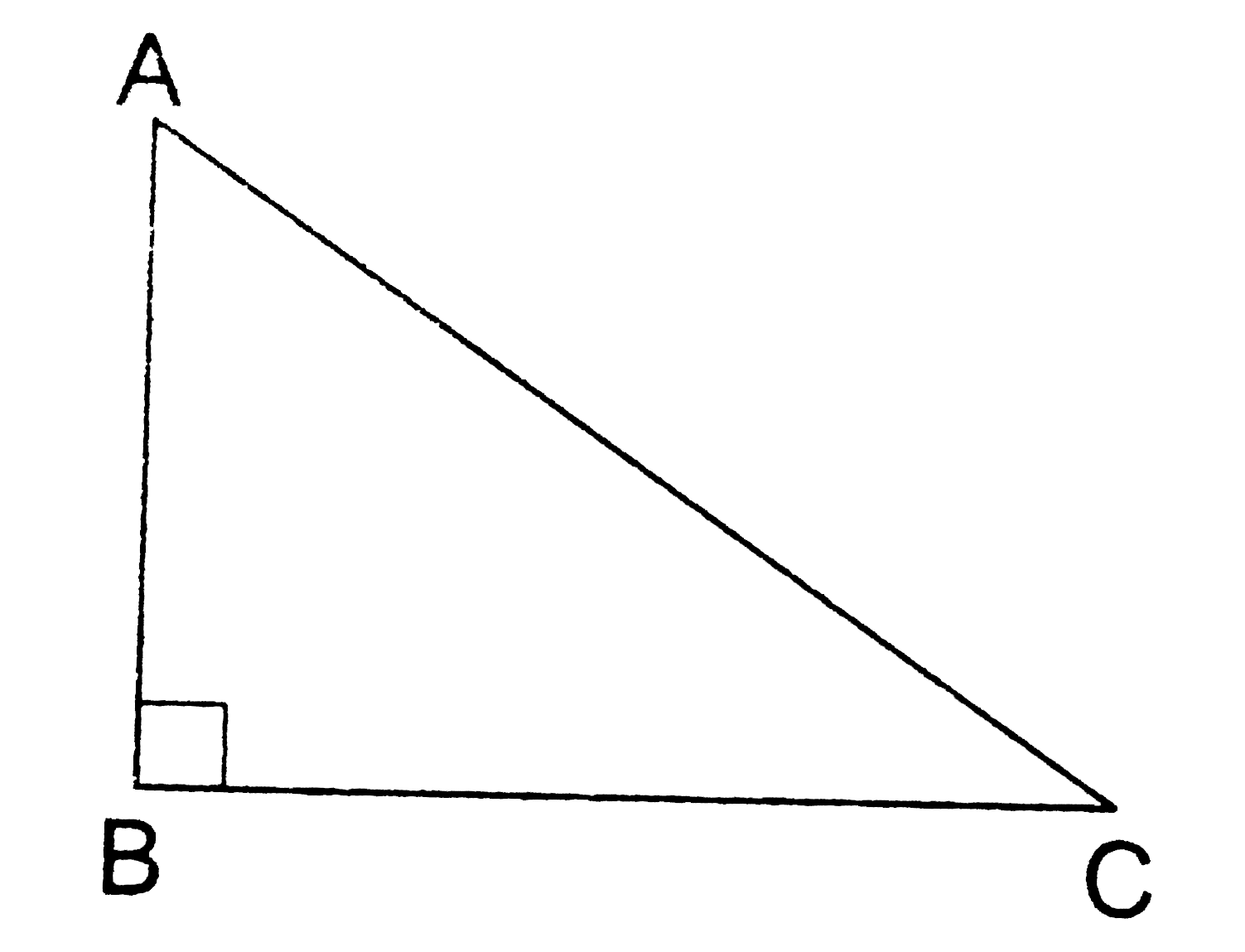
Let ABC be a right triangle in which ∠B=90∘.
Then, ∠A+∠C=90∘.
∴ ∠B>∠Aand∠B>∠C
⇒ AC>BCandAC>AB (Side opposite to larger angle is longer).
∴ With the help of theorem (7.6) hum ye keh sakte hai AC is the longest side.
Hence, in a right triangle, the hypotenuse is the longest side.
Theorem 7.7
In any triangle, the side opposite to the larger (greater) angle is longer.
Let we have triangle ABC such that ∠C>∠B
if AC>AB then from theorem 7.6 we have ∠B>∠C but we have ∠C>∠B
Therefore by contradiction we have AB>AC.
Theorem 7.8
The sum of any two sides of a triangle is greater than the third side.
Let in triangle ABC, side BA is produce to D such that AD=AC. 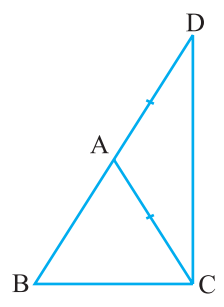
∠ACD=∠CAD (from theorem 7.2)
∴∠ACD+∠ACB>∠CAD
∴∠BCD>∠CAD
∴BD>BC (from theorem 7.7)
Or, BA+AD>BC
BA+AC>BC (AD=AC)
∴AB+AC>BC
Similarly we can prove AB+BC>AC, BC+AC>AB.
Example 10
In the adjoining figure, ABC is a triangle and D is any point in its interior. Show that (BD+DC)<(AB+AC).
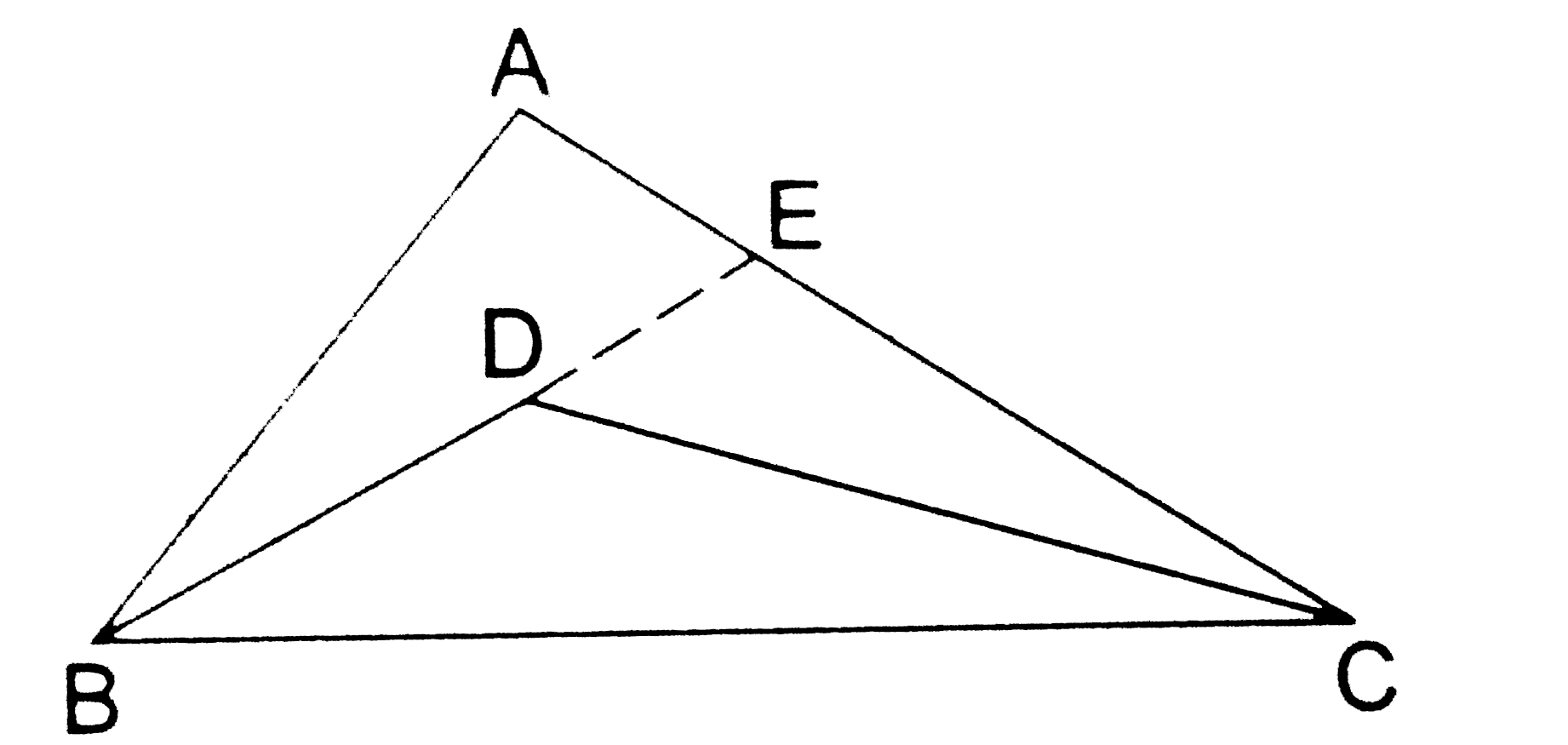
CONSTRUCTION : Produce BD to meet AC at E.
To prove (BD+DC)<(AB+AC).
We know that in a triangle, the sum of any two sides is always greater than the third side.
In ∴ΔABE, we have
AB+AE>BE⇒AB+AE>BD+DE ...(i)
In ΔCDE, we have
DE+EC>DC. ...(ii)
From (i) and (ii), we get
AB+AE+DE+EC>BD+DE+DC
⇒ AB+(AE+EC)>BD+DC
⇒ (AB+AC)>(BD+DC).
Hence, (BD+DC)<(AB+AC).
Summary
1. Two figures are congruent, if they are of the same shape and of the same size.
2. Two circles of the same radii are congruent.
3. Two squares of the same sides are congruent.
4. If two triangles ABC and PQR are congruent under the correspondence A ↔ P, B ↔ Q and C ↔ R, then symbolically, it is expressed as Δ ABC ≅ Δ PQR.
5. If two sides and the included angle of one triangle are equal to two sides and the included angle of the other triangle, then the two triangles are congruent (SAS Congruence Rule).
6. If two angles and the included side of one triangle are equal to two angles and the included side of the other triangle, then the two triangles are congruent (ASA Congruence Rule).
7. If two angles and one side of one triangle are equal to two angles and the corresponding side of the other triangle, then the two triangles are congruent (AAS Congruence Rule).
8. Angles opposite to equal sides of a triangle are equal.
9. Sides opposite to equal angles of a triangle are equal.
10. Each angle of an equilateral triangle is of 60°.
11. If three sides of one triangle are equal to three sides of the other triangle, then the two triangles are congruent (SSS Congruence Rule).
12. If in two right triangles, hypotenuse and one side of a triangle are equal to the hypotenuse and one side of other triangle, then the two triangles are congruent (RHS Congruence Rule).
13. In a triangle, angle opposite to the longer side is larger (greater).
14. In a triangle, side opposite to the larger (greater) angle is longer.
15. Sum of any two sides of a triangle is greater than the third side.