QUADRILATERALS for Class 9 MATHS

Bacchon, jab hum apne charo taraf dekhte hai to hum pate hai ki aise bahut sare objects hai jinme four sides and four corners hote hai for example : the floor, walls, ceiling, windows of your classroom, the blackboard etc. So guys, aapne previous chapter me triangles and unke properties ke bare me pdha hai jisme three sides and three vertices hote the. Lakin es chapter me hum aise figures and unke properties ke bare me padhne wale hai jinke four sides and four vertices hote hai jinhe quadrilaterals kha jata hai. In this chapter, we will study more about different types of quadrilaterals, their properties and especially those of parallelograms. Although most of the objects we see around are of the shape of a special quadrilateral called a rectangle, we shall study more about quadrilaterals and especially parallelograms because a rectangle is also a parallelogram and all properties of a parallelogram are true for a rectangle as well.

The sum of the angles of a quadrilateral is ${360}^{\circ }$.

So bacchon, verify karne ke liye let us assume a quadrilateral $ABCD$. Now, draw a diagonal $AC$ jo quadrilateral ko two triangles me divide karta hai.

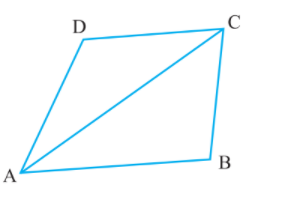
Here in $△ADC$
$\angle DAC+\angle ACD+\angle D=180°$ [Angle sum property of triangle]
Similarly in $△ABC$
$\angle CAB+\angle ACB+\angle B=180°$ [Angle sum property of triangle]
Now, adding both the above equations
$\angle DAC+\angle ACD+\angle D+\angle CAB+\angle ACB+\angle B=180°+180°=360°$
Here, $\angle DAC+\angle CAB=\angle A\text{and}\angle ACD+\angle ACB=\angle C$
$\therefore \angle A+\angle D+\angle B+\angle C=360°.$
So guys, humne dekha ki kise bhi quadrilaterals ke angles ka sum ${360}^{\circ }$ hota hai.

Jaisa ki hum jante hai quadrilaterals are those figures in which we have four sides and four vertices. Look at the different quadrilaterals drawn below :

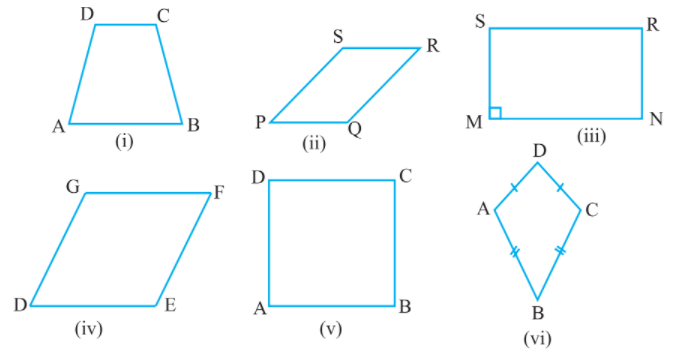
Upar hum bahut sare quadrilaterals ke example dekh sakte hai jinki alag alag properties hai. So guys, if we go through these figures one by one we can observe that :

There are few properties of Parallelogram jinme se kuch ke bare humne previous classes me bhi pdha hai. Is chapter me hum en properties ko detail me, as a theorem padhenge and also we will prove some of them jo aksar aapke exams me bhi puch liye jate hai.

A diagonal of a parallelogram divides it into two congruent triangles.

Let $ABCD$ be a parallelogram and $AC$ be a diagonal.

$AC$ divides parallelogram $ABCD$ into two triangles, namely, $\Delta ABC$ and $\Delta CDA$. We need to prove that these triangles are congruent.
In $△ABC$ and $△CDA$ we observe that $BC\mid \mid AD$ and $AC$ is a transversal.
$\therefore \angle BCA=\angle DAC$ [Alternate interior angles]
Similarly $AB\mid \mid DC$ and $AC$ is a transversal.
$\therefore \angle BAC=\angle DCA$ [Alternate interior angles]
And $AC=CA$ [Common]
$\therefore \Delta ABC\cong \Delta CDA$ [ASA rule ]
So we have proved that diagonal $AC$ divides parallelogram $ABCD$ into two congruent triangles $ABC$ and $CDA$.

In a parallelogram, opposite sides are equal.

So guys, jaisa ki humne previous theorem me dekha hai ki diagonal divides the parallelogram in two congruent triangles.

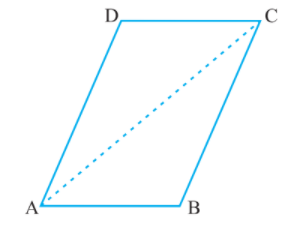
As we know that corresponding parts of congruent triangles are also same.
So, $AB=DC\text{and}AD=BC$

If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.

Let us consider a quadrilateral $ABCD$.

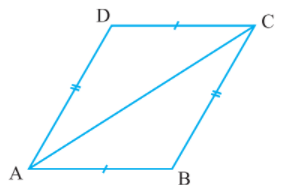
It is given that sides $AB\text{and}CD$ of the quadrilateral $ABCD$ be equal and also $AD=BC$.
In $△ABC\text{and}△CDA$,
$AB=CD$ [given]
$BC=DA$ [given]
And $AC=AC$ [common]
$\therefore △ABC\cong △CDA$ [SSS rule]
So, $\angle BAC=\angle DCA$ [C.P.C.T.] ,
and $\angle BCA=\angle DAC$ [C.P.C.T] .
So guys jaisa ki hum yha dekh sakte hai $AC$ ia a transversal for $AB$ and $CD$ and we have proved that alternate interior angles are same so $AB\mid \mid CD$.
Similarly $AC$ is a transversal for $BC$ and $DA$ and alternate interior angles are same so $BC\mid \mid DA$.
Hence, $ABCD$ is a parallelogram.

In a parallelogram, opposite angles are equal.

Let us consider a parallelogram $ABCD$.

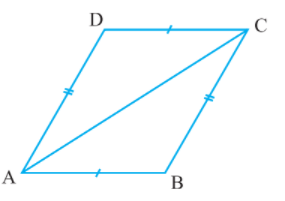
Guys jaisa ki humne theorem 8.1 me dekha hai ki a diagonal divides a parallelogram into two congruent triangles. Which means for diagonal $AC$,
$\Delta ABC\cong \Delta CDA$ Since corresponding parts of congruent triangles are same therefore
$\angle D=\angle B$
Similarly if we draw a diagonal $BD$ we can easily prove that $△ABD\cong △CDB$.
Well, in that case $\angle A=\angle C$.
$\therefore$ Each pair of opposite angles is equal.

If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.

This is the reverse of the previous theorem.

The diagonals of a parallelogram bisect each other.

Let us consider a parallelogram $ABCD$ where $AC$ is a diagonal .

Here we have to prove that $OA=OC$ and $OB=OD$ .
Since we have $AD\mid \mid CB$ and $BD$ and $AC$ work as transversals.
$\Rightarrow \angle ADO=\angle CBO$ [alternate interior angles]
Similarly $\angle OCB=\angle OAD$ [alternate interior angles]
$AD=BC$ [opposite sides are equal in a parallelogram]
$\therefore △AOD\cong △COB$ [ASA rule]
Therefore from CPCT $OA=OC$ and $OB=OD$ proved.

If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.

Let us consider a quadrilateral $ABCD$ in which $AC$ and $BD$ are two diagonals such that $OA=OC$ and $OB=OD$

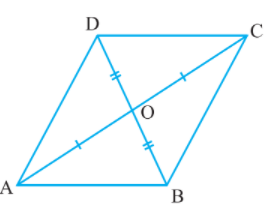
Here we have to prove that $AB\mid \mid CD$ and $BC\mid \mid AD$
In $△AOD$ and $△COB$
$OA=OC$ [given]
$OB=OD$ [given]
$\angle AOD=\angle COB$ [opposite angles ]
$\therefore △AOD\cong △COB$
$\Rightarrow \angle ABO=\angle CDO$ [CPCT]
Here we can see that alternate interior angles are same
$\therefore AB\mid \mid CD$
Similarly $\angle OAD=\angle OCB$ [CPCT]
$\therefore BC\mid \mid AD$ [because alternate interior angles are same]
Therefore we can conclude that $ABCD$ is a parallelogram.

Show that the diagonals of a rhombus are perpendicular to each other.

Consider the rhombus $ABCD$, such that $AC$ and $BD$ are two diagonals. They cut each other at point $O$.

We know that for a rhombus $AB=BC=CD=DA$
Now, in $\Delta AOD$ and $\Delta COD$,
$OA=OC$ [Diagonals of a parallelogram bisect each other]
$OD=OD$ [Common]
and $AD=CD$
$\therefore \Delta AOD\cong \Delta COD$ [SSS congruence rule]
This gives, $\angle AOD=\angle COD$ [CPCT]
But, $\angle AOD+\angle COD=180°$ [Linear pair]
$\therefore 2\angle AOD=180°$
$\Rightarrow \angle AOD=90°$
So guys, finally we can conclude that the diagonals of a rhombus are perpendicular to each other.

$ABC$ is an isosceles triangle in which $AB=AC$. $AD$ bisects exterior angle $PAC$ and $CD\mid \mid AB$. Show that (i)$\angle DAC=\angle BCA$ and (ii) $ABCD$ is a parallelogram.

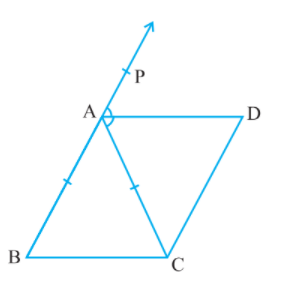
(i) $\Delta ABC$ is isosceles in which $AB=AC$ [Given]
$\therefore \angle ABC=\angle ACB$ [Angles opposite to equal sides]
Also, $\angle PAC=\angle ABC+\angle ACB$ [Exterior angle of a triangle]
$\therefore \angle PAC=2\angle ACB$ …………(i)
Now, hume pta hai $AD$ bisects $\angle PAC$.
So, $\angle PAC=2\angle DAC$...........(ii)
$\therefore 2\angle DAC=2\angle ACB$ [From (1) and (2)]
$\Rightarrow \angle DAC=\angle ACB$
(ii) Now, these equal angles form a pair of alternate angles when line segments $BC$ and $AD$ are intersected by a transversal $AC$ .
So, $BC\mid \mid AD$
Also, $BA\mid \mid CD$ [Given]
$\therefore ABCD$ is a parallelogram.

Two parallel lines $l$ and $m$ are intersected by a transversal $p$.

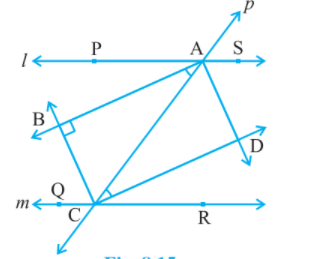
Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.

It is given that $PS\mid \mid QR$ and transversal $p$ intersects them at points $A$ and $C$ respectively .
The bisectors of $\angle PAC$ and $\angle ACQ$ intersect at $B$ and bisectors of $\angle ACR$ and $\angle SAC$ intersect at $D$.
Hume ye prove karna hai $ABCD$ is a rectangle.
Now, $\angle PAC=\angle ACR$ [Alternate angles as $l\mid \mid m$ and $p$ is a transversal]
So,$\frac{1}{2}\angle PAC=\frac{1}{2}\angle ACR$
$\therefore \angle BAC=\angle ACD$
Guys, yha hum dhyan denge these form a pair of alternate angles for lines $AB$ and $DC$ with $AC$ as transversal and they are equal also.
$\therefore AB\mid \mid DC$
Similarly, $BC\mid \mid AD$ [Considering $\angle ACB$ and $\angle CAD$]
$\therefore$ Quadrilateral $ABCD$ is a parallelogram.
Now, $\angle PAC+\angle CAS=180°$ [Linear pair]
$\therefore \left(\frac{1}{2}\right)\angle PAC+\left(\frac{1}{2}\right)\angle CAS=\left(\frac{1}{2}\right)\times 180°=90°$
Or $\angle BAC+\angle CAD=90°$
$\therefore \angle BAD=90°$
So, $ABCD$ is a parallelogram in which one angle is $90°$.
Therefore, $ABCD$ is a rectangle.

A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.

Let us consider a quadrilateral $ABCD$.

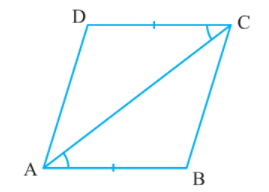
Here we have given that $AB=CD$ and $AB\mid \mid CD$.
Let us draw a diagonal $AC$.
So, $AB=CD$ [given]
$\angle BAC=\angle DCA$ [ $AB\mid \mid CD$ and $AC$ is a transversal]
$AC=AC$ [common]
$\therefore$ $\Delta ABC\cong \Delta CDA$ by $SAS$ congruence rule. $\therefore \angle CAD=\angle ACB$ [CPCT]
Since these angles are alternate interior angles for $AC$ as a transversal for two lines $AD$ and $BC$.
$\therefore AD\mid \mid BC$
Hence we can conclude that $ABCD$ is a parallelogram.

$ABCD$ is a parallelogram in which $P$ and $Q$ are mid-points of opposite sides $AB$ and $CD$(see Fig.) . If $AQ$ intersects $DP$ at $S$ and $BQ$ intersects $CP$ at $R$, show that : $APCQ$ is a parallelogram.

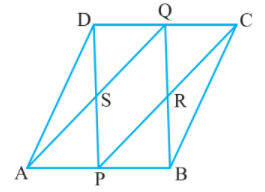
In quadrilateral $APCQ$,
$AP\mid \mid QC$ [Since AB || CD]..........(i)
also $AP=\frac{1}{2}AB$ and $CQ=\frac{1}{2}CD$ [given]
also $AB=CD$ [opposite sides of parallelogram are equal]
$\therefore AP=QC$.............(ii)
Therefore From (i) and (ii) and Theorem 8.8 we can say that
$APCQ$ is a parallelogram.

Statement : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.

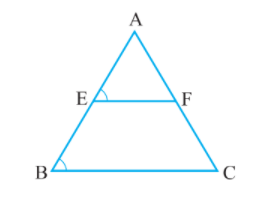
Let us consider a triangle $ABC$ such that $E$ and $F$ are mid-points of $AB$ and $AC$ respectively.

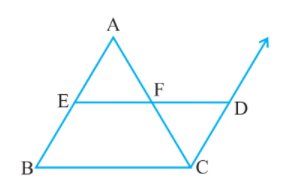
CONSTRUCTION : Draw $CD$ such that CD || BA .
We have to prove that $EF\mid \mid BC$
Now we have
$AE=EB$ [$E$ is mid point of $AB$]
$AF=FC$ [$F$ is mid point of $AC$]
In $△AEF$ and $△CDF$
$\angle EAF=\angle DCF$[alternate interior angles]
$AF=FC$
$\angle AFE=\angle CFD$ [vertically opposite angle ]
$\therefore △AEF=△CDF$[ASA rule]
But guys agar hum yha dhyan de to hum observe karte hai
$AE=CD$ [CPCT]
and $AE=EB$ [given]
$\therefore EB=CD$
and also $EB\mid \mid CD$[construction]
So guys jaisa ki hum jante hai agar kisi quadrilateral me two opposite sides parallel and equal hote hai to that quadrilateral is nothing but a parallelogram.
$\Rightarrow ED\mid \mid BC$
Or,$EF\mid \mid BC$ [Proved]

The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.

Let us consider a triangle $ABC$ such that $E$ is the mid-point of $AB$ , line $l$ is passing through $E$ and is parallel to $BC$ and $CM\mid \mid BA$ .

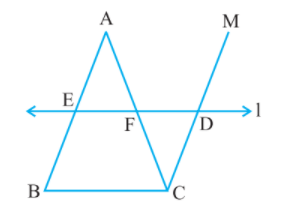
Here we have to prove that $AF=CF$.
Taking $△AEF\text{and}△CDF$
Here , $\angle EAF=\angle DCF$ [alternate interior angles]
$EB=CD$ [construction]
and $EB=EA$ [given]
$\Rightarrow EA=CD$ Also $\angle AFE=\angle CFD$ [vertically opposite angles]
$\therefore △AFE\cong △CFD$
So with the property of CPCT hum ye conclude kar sakte hai
$AF=FC$
$\Rightarrow F$ is the midpoint of $AC$.

In $\Delta ABC,D,E\text{and}F$ are respectively the mid-points of sides $AB$, $BC$ and $CA$ (see Fig.). Show that $\Delta ABC$ is divided into four congruent triangles by joining $D,E\text{and}F$.

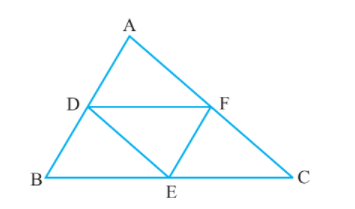
As $D$ and $E$ are mid-points of sides $AB$ and $BC$ of the triangle $ABC$, by Theorem 8.9,
$DE\mid \mid AC$
Similarly $DF\left|\left|BC\text{and}EF\right|\right|AB$
Therefore $ADEF,BDFE\text{and}DFCE$ are all parallelograms.
Now $DE$ is a diagonal of the parallelogram $BDFE$,
$\therefore \Delta BDE\cong \Delta FED$
Similarly $\Delta DAF\cong \Delta FED$
and $\Delta EFC\cong \Delta FED$
So, all the four triangles are congruent.

In this chapter, you have studied the following points :
1. Sum of the angles of a quadrilateral is $360°$.
2. A diagonal of a parallelogram divides it into two congruent triangles.
3. In a parallelogram,
(i) opposite sides are equal
(ii) opposite angles are equal
(iii) diagonals bisect each other.
4. A quadrilateral is a parallelogram, if one of the following condition satisfied :
(i) opposite sides are equal
(ii) opposite angles are equal
(iii) diagonals bisect each other
(iv) a pair of opposite sides is equal and parallel
5. Diagonals of a rectangle bisect each other and are equal and vice-versa .
6. Diagonals of a rhombus bisect each other at right angles and vice-versa .
7. Diagonals of a square bisect each other at right angles and are equal, and vice-versa.
8. The line-segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it.
9. A line through the mid-point of a side of a triangle parallel to another side bisects the third side.
10. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral, in order, is a parallelogram.