POLYNOMIALS for Class 9 MATHS

A polynomial is an Algebraic expression with combination of constants and variables where power of variables are non negative integers. For example : $3x^2+x-5=0$, $x^2-4x+7$ etc.

A polynomial in one variable $x$ is an algebraic expression of the form
$p\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+a_{n-2}{x}^{n-2}+.......+a_2{x}^2+a_{1}x+a_0$ where $n$ is an non negative integer and $a_0,a_1,a_2,a_3,.......,a_n$ are constants and $a_n\ne 0$

In algebra two types of symbols are used Constants and Variables. Where letters like $x$, $y$, $z$, etc. are used to denote variables. $2x$, $-x$, $\left(\frac{1}{5}\right)x$ are algebraic expressions in form of (a constant) $\times$ (a variable). The values of constant will remain same while the variable will keep changing.

The several parts of a polynomial separated by ‘+’ or ‘-‘ operations are called the terms of the expression.

Coefficient :
Any factor of a term is called the coefficient of the remaining term.
For example
In $7x$, $7$ is coefficient of $x$.
In $-5x^{2}y$, $5$ is coefficient of $-x^{2}y$, $-5$ is coefficient of $x^{2}y$.

If the variable in a polynomial is $x$, we can denote polynomial by $p\left(x\right)=3x^2-7x+2$, $p\left(x\right)$ denotes $p$ is some polynomial in $x$, we can also use any name to denote polynomial like $p\left(x\right),q\left(x\right),r\left(x\right),s\left(x\right)$ etc. If variable polynomial is $y$, then
$p\left(y\right)=3y^2-7y+2$.

$\sqrt{x}+5,x+\frac{2}{x}\sqrt[3]{3y}+y^2$, etc are not a polynomial because they don’t have exponent as whole number.

Polynomials are classified in two ways
(i) On the basis of number of terms.
(ii) On the basis of degree.

A polynomial can have any (finite) number of terms. For example, $x^{100}+x^{99}+x^{98}+\dots +x^2+x+1$ is polynomial with 101 terms.

(i) Monomial : If polynomial have only one term i.e. $4x,2x^3,y^2,u^8$. Polynomials having only one term are called monomials (‘mono’ means ‘one’).

(ii) Binomial : Polynomials having only two terms are called binomials (‘bi’ means ‘two’). For example, $4x+5,2x^3-7x,y^2+7y,u^8+u^3$.

(iii) Trinomial : Similarly, polynomials having only three terms are called trinomials (‘tri’ means ‘three’). For example, $4x^2+5x+6,2x^3-7x+9,y^3+7y^2+y,u^8+u^3+1$

The algebraic expressions like $8x,4y-3,8x^2+5,y^2-5y+6$ etc. each of which involves only one variable are called polynomials in one variable.

Polynomials in two or more variables :
An algebraic expression, whose term involve two or more variables such that the exponent of each variable is a whole number, is called a polynomial in two or more variables.
For example :
(i) $3x^2-6xy+8y^2$ is a polynomial in two variables in $x$ and $y$.
(ii) $x+x{y}^3-8x^{2}yz-15$ is a polynomial in three variables $x,y$ and $z$.

In polynomial, $2x^3-7x+9$ highest exponent of x is 3. Similarly, in $u^8+u^3+1$ highest exponent of u is 8.
The highest power of the variable in a polynomial is called degree of polynomial.
So, degree of polynomial of $2x^3-7x+9$ is 3 and of $u^8+u^3+1$ is 8.

(i) Constant polynomial : A polynomial with degree $0$ (zero) is called constant polynomial.
For example, $8,34,-4,\pi ,7,5$ etc.
The constant polynomial $0$ is called the zero polynomial.
Note : $\to$ The degree of zero polynomial is not defined.

(ii) Linear Polynomial : A polynomial of degree one is called a linear polynomial.
For example, $2x–1,2-y,\sqrt{5}u+7$ etc.

(iii) Quadratic Polynomial : A polynomial of degree two is called a quadratic polynomial.
For example, $6x^2,y^2,\frac{2}{5}{z}^2,x^2+6$ etc.

(iv) Cubic Polynomial : A polynomial of degree three is called a cubic polynomial.
For example, $3y^2+y^3,x^3-2x+7$etc.

Value of a polynomial $p\left(x\right)$ at $x=a$ is $p\left(a\right).$
e.g., If $p\left(x\right)=x^2+2x+6$ then, at $x=2,p\left(2\right)=22+2\times 2+6=14$

Assume we have
$p\left(x\right)=2x^3+6x^2-9x-13$
If we replace $x$ by $1$ in $p\left(x\right)$, we get
$p\left(1\right)=2\times {\left(1\right)}^3+6\times {\left(1\right)}^2-9\times \left(1\right)-13$
$=2+6-9-13$
$=-14$
So we can say $p\left(x\right)=-14$ at $x=1$.
When $x=0$,
$p\left(0\right)=2\times {\left(0\right)}^3+6\times {\left(0\right)}^2-9\times \left(0\right)-13$
$=-13$
When $x=-1$,
$p(-1)=2\times {(-1)}^3+6\times {(-1)}^2-9\times (-1)-13$
$=-2+6+9–13$
$=0$
So, whenever polynomial becomes zero by putting value of $x$ is called zero of polynomial. And value of $x$ is called root of polynomial.
Here we have $x=-1$ as our root.
Note:$\to$ A non-zero constant polynomial has no zero and every real number is a zero of the zero polynomial.

Let $p\left(x\right)$ be any polynomial of degree $n$ greater than or equal to one $(n\ge 1)$ and let a be any real number. If $p\left(x\right)$ is divided by the linear polynomial $x–a$, then the remainder is $p\left(a\right).$

Dividing $p\left(x\right)$ by $g\left(x\right)$, where $p\left(x\right)=x+3x^2–1$ and $g\left(x\right)=1+x$
Step 1 :$\to$ We write the dividend $x+3x^2–1$ and the divisor $1+x$ in the standard form, i.e., after arranging the terms in the descending order of their degrees. So, the dividend is $3x^2+x–1$ and divisor is $x+1$.
Step 2 :$\to$ We divide the first term of the dividend by the first term of the divisor, i.e., we divide $3x^2$ by $x$, and get $3x$. This gives us the first term of the quotient.
$\frac{3x^2}{x}=3x=$ first term of quotient
Step 3 :$\to$ We multiply the divisor by the first term of the quotient, and subtract this product from the dividend, i.e., we multiply $x+1$ by $3x$ and subtract the product $3x^2+3x$ from the dividend $3x^2+x–1$. This gives us the remainder as $–2x–1$.

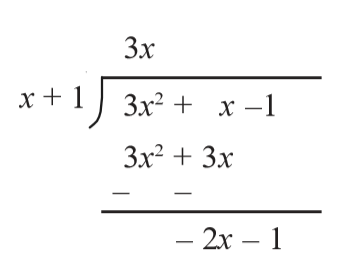
Step 4 :$\to$ We treat the remainder $–2x–1$ as the new dividend. The divisor remains the same. We repeat Step 2 to get the next term of the quotient, i.e., we divide the first term $–2x$ of the (new) dividend by the first term $x$ of the divisor and obtain $–2$. Thus, $–2$ is the second term in the quotient.
$\frac{–2x}{x}=–2=$ second term of quotient
New Quotient $=3x–2$
Step 5 :$\to$ We multiply the divisor by the second term of the quotient and subtract the product from the dividend. That is, we multiply $x+1$ by $–2$ and subtract the product $–2x–2$ from the dividend $–2x–1$. This gives us $1$ as the remainder.
This process continues till the degree of the new dividend is less than the degree of the divisor. At this stage, this new dividend becomes the remainder and the sum of the quotients gives us the whole quotient.

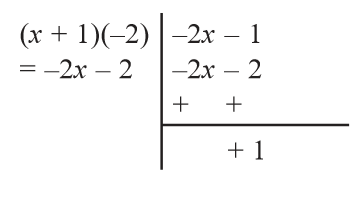
Step 6 :$\to$ Thus, the quotient in full is 3x – 2 and the remainder is 1. Let us look at what we have done in the process above as a whole:

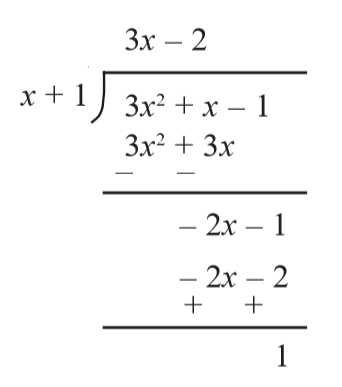
Notice that $3x^2+x–1=(x+1)(3x–2)+1$

Dividend = (Divisor × Quotient) + Remainder

Let $q\left(x\right)$ be a polynomial of degree n ≥ 1 and a be any real number, then
$\left(i\right)(x–a)$ is a factor of $q\left(x\right),$ if $q\left(a\right)=0$ and

$\left(ii\right)$ $q\left(a\right)=0,$ if $x–a$ is a factor of $q\left(x\right).$

$\left(i\right)$ By splitting the middle term : Suppose a quadratic polynomial is $x^2+lx+m$ where $l$ and $m$ are constants. Now, we split the middle term $lx$ as $ax+bx,$ so that $ab=m.$ Then,
$x^2+lx+m=x^2+ax+bx+ab=x(x+a)+b(x+a)=(x+a)(x+b)$

$\left(ii\right)$ By using factor theorem : Suppose, $a{x}^2+bx+c$ be a quadratic polynomial. Let two factors be $(x–\alpha )$ and $(x–\beta )$
$\therefore a(x–\alpha )(x–\beta )=a{x}^2+bx+c$
$\Rightarrow a{x}^2–a(\alpha +\beta )x+a\alpha \beta =a{x}^2+bx+c$
On equating the coefficient of x and constant term.
We get, α + β = $-\frac{b}{a}$ and αβ = $\frac{c}{a}$
On simplifying, we get the values of $\alpha$ and $\beta .$

(iii) The factorisation of cubic polynomials : The splitting middle term method is not applicable for cubic polynomials. Its need to find at least one factor first, and then adjust the given polynomial such that it becomes the product of term in which one of them is that factor and the other is a quadratic polynomial. Now, solve this quadratic polynomial by the previous method.

i. ${(x+y)}^2=x^2+2xy+y^2$
ii. ${(x-y)}^2=x^2-2xy+y^2$
iii. $(x+a)(x+b)=x^2+(a+b)x+ab$
iv. $x^2-y^2=(x+y)(x-y)$
v. ${(x+y+z)}^2=x^2+y^2+z^2+2xy+2yz+2xz$
vi. ${(x+y)}^3=x^3+y^3+3xy(x+y)$
$\text{or},{(x+y)}^3=x^3+y^3+3x^{2}y+3x{y}^2$
vii. ${(x-y)}^3=x^3-y^3-3xy(x-y)$
$\text{or},{(x-y)}^3=x^3-y^3-3x^{2}y+3x{y}^2$
viii. $x^3+y^3+z^3-3xyz$
$=(x+y+z)(x^2+y^2+z^2-xy-yz-xz)$
ix. $x^3+y^3=(x+y)(x^2-xy+y^2)$
x. $x^3-y^3=(x-y)(x^2+xy+y^2)$

So guys jaisa ki hamne previous classes me Algebra me constant , variables, coefficients and algebraic expressions ke baare me padha tha . Ab hum us Algebra ke knowledge ko next level par le jane wale hai. Jisme hum ek naye chiz ke bare me padhne wale hai jiska naam hai Polynomials. Sath hi sath hum padhne wale hai , Different types of polynomials , Zeros of Polynomials , Remainder Theorem , Factor theorem and factorization , Some important formula or algebraic identity.

Algebraic Expression : Combination of some constants, variables along with one or more operations i.e. $x^2-4x+7$ is called algebraic expression.
Is expression me, we have three terms $x^2$, $-4x$ and $7$, where $x$ is called variables. Ek baat ka dhyan rakhenge ki $x$ ke alawa koi bhi letter hum variable ke place par le sakte hai. e.g. $x,y,z,p,q,r,s,t$, and so on. Variable ke sath jo bhi constant term multiplied hote hain unhe kha jata hai coefficients of that variable.
Some more examples of Algebraic expressions are $9\sqrt{x}+5$, $5x^3+9y+7$, $\frac{7}{5}{x}^{-5}+x^{-3}+2x^3$.
Constant : In mathematics, wo mathematical quantity jiski value hamesha same rehne wali hai kise bhi situation me unko constant kehte hai. For example : $2+2=4$. Yha hum dekh sakte hai, har situation me hume 4 hi milne wali hai. Ye kbhi 5 nahi ho jayega .
Variables : Wo mathematical quantity jiski value according to the situation vary ya change karne wali hai. For example : Man lo maine aap logon se puch liya ki please tell me height of your's from 5 years uptill now, tab kya apki height fix hai tab se ab tak , aap kahenge nahi. Toh aisi sabhi quantities jinki values fix nahi hoti unki variable kehte hai.

Polynomials are nothing but special type of Algebraic expressions which consist variables and coefficients but isme variable ki power will always be a positive integer including zero. (i.e. 0, 1, 2, 3.....).
For Ex : $3x^2+x-5=0$ is a Polynomial with variable $x$. Where coefficient of $x^2=3$, and coefficient of $x=1$.
$5\sqrt{x}+9x^2=0$ is not a polynomial because the variables $x$ has power in fraction.

Which one of the following is a polynomial ?
(a) $\frac{x^2}{2}-\frac{2}{x^2}=\frac{x^2}{2}-2x^{-2}$
(b) $\sqrt{2x}-1$
(c) $x^2+\frac{3x^{\frac{3}{2}}}{\sqrt{x}}$
(d) $\frac{x-1}{x+1}$

(a) Now $\frac{x^2}{2}-\frac{2}{x^2}=\frac{x^2}{2}-2x^{-2}$ , it is not a polynomial , because exponent of $x$ is $-2$ which is not a whole number .
(b) Now, $\sqrt{2x}-1=\sqrt{2}\times x^{1/2}$ =1, it is not a polynomial, because exponent of $x$ is $-\frac{1}{2}$ which is not a whole number .
( c) Now, $x^2+\frac{3x^{\frac{3}{2}}}{\sqrt{x}}=x^2+3x^{\frac{3}{2}-\frac{1}{2}}=x^2+3x^{\frac{2}{2}}=x^2+3x,$ it is a polynomial because exponent of $x$ is a whole number.
(d) $\frac{x-1}{x+1}$ , it is not a polynomial because it is a rational function.

So guys ab aap ye jante hai ki polynomials are special combination of constants and variables. To waise polynomials jisme sirf ek variable ho to waise polynomials ko polynomials in one variable kehte hai.
Ex : $7x^5+4x^3+5x^2+7=0$
In the above example we have a single variable that is $x$, iska matlab humara given example polynomials in one variable wala hai. Now agar hmare pas aisa koi polynomial hota
Ex : $7x^5+4y^3+5x^2+7=0$, is example me ham dekh sakte hai we have two variables $x$ and $y$ so this example is a polynomial with two variables.
So guys chlo Polynomials ke bare or kuch interesting baten jante hai. Is chapter me hume polynomials in one variable ke bare hi padhna hai to chlo shuru kate hai with some terminologies.
Degree of Polynomials :
Kise bhi Polynomial me variable ki highest power will be degree of that polynomial.
Ex: $9x^7+7x^5+5x^3+9=0$
Here highest power of variable $x$ is $7$. So degree is $7$.
Constant Polynomials : Kya ham kise constant, let $5$ ko aise likh sakte hain $5x^0$, because $x^0=1$.
Yes, we can write $5=5x^0$.
Iska matlab, kise bhi constant ko hum polynomial ke form me likh sakte hai, such type of polynomials are called constant polynomial.
Zero Polynomial : Ye dekhna bahut hi interesting hai ki zero ko bhi hum polynomial ke form me likh sakte hai like, $0x^0$ or $0x^1$ or $0x^2$ and so on.
So zero can also be written as polynomial which is known as zero polynomial.
Note: kise bhi variable ki koi bhi power kyu na ho use $0$ se multiply krne se result will be $0$. So degree of Zero polynomial can not be defined.

Degree of the polynomial $4x^4+0x^3+0x^5+5x+7$ is

Degree of $4x^4+0x^3+0x^5+5x+7$ is equal to the highest power of variable $x$.
Here, the highest of $x$ is 4.
Hence, the degree of a polynomial is $4$.

Guys Polynomials ko hum two ways me classify kr sakte hai .
1. On the basis of number of terms
2. On the basis of Degree.

On the basis of number of terms.
(i) Monomial : Mono ka matlab hota hai one which means aisa polynomial jisme single term ho .
for Ex: $7x^2,5x,9x^7$
(ii) Binomial : Ek aisa polynomial jisme two terms ho.
for Ex: $3x^3+6,3x+7,9x^2+5x$
(iii) Trinomial : Ek aisa polynomial jisme exactly three terms ho.
For Ex : $4x^3+6x+9$, $8x^4+9x^3+7x^2$
And so on........
On the Basis of degree :
(i) Linear Polynomial : Ek aisa polynomial jisme variable ki highest power ya degree, one ho then that is called linear polynomial.
for Ex: $7x+3,9x,6x+12$.
(ii) Quadratic Polynomial : Ek aisa polynomial jisme variable ki highest power ya degree, two ho that is called quadratic polynomial.
For Ex : $4x^2+5x,9x^2,6x^2-x-1$.
(iii) Cubic Polynomial : Ek aisa polynomial jisme variable ki highest power ya degree, three ho that is called cubic polynomial.
for Ex: $9x^3+6x^2+12x-1,7x^3-2,12x^3$.
Jaisa ki ham dekh sakte hai according to degree hum polynomial ko further classify kar sakte hai jaise if degree is $4$ then that type of polynomial are called Biquadratic Polynomial and so on.

Classify the following polynomials as polynomials in one variable, two variables etc.
(1) $x^2+x+1$ (ii) $y^3-5y$
(iii) $xy+yz+zx$ (iv) $x^2-2xy+y^2+1$

(i) polynomial $x^2+x+1$ is a one various polynomial, because it contains only one variable i.e., x.
(ii) Polynomial $y^3-5y$ is a one variable polynomial, because it contains only one variable i.e., y.
(iii) Polynomial $xy+yz+zx$ is a three variable polynomial, because it contains three variables x, y and z.
(iv) polynomial $x^2-2xy+y^2+1$ is a two variables polynomial, because it contains two variables x and y.

If the Variable in a Polynomial is $x$, we may denote the polynomial by $p\left(x\right),\text{or}q\left(x\right),\text{or}r\left(x\right)$ etc.
For Ex : $p\left(x\right)=2x^3+5x$
$q\left(x\right)=9x^3+4x^2+5x$
Similarly if the variable in a polynomial is $y$, We may denote the polynomial by $p\left(y\right)$or $q\left(y\right)$, etc.
Ab hum value of polynomial ki baat krne wale hai jo bahut hi interesting hone wala hai.
Now what will be the value of a polynomial at a given value of variable :
Let hmare pas $x$ variable wala ek polynomial hai i.e. $p\left(x\right)=4x^3-7x^2+5x+9$.
Kya hum $x=2$ par Polynomial ki value bta sakte hai ? Answer is yes, Just we have to replace $x$ with $2$ in the given equation.
Given $p\left(x\right)=4x^3-7x^2+5x+9$
So, $p\left(2\right)=4\times 2^3-7\times 2^2+5\times 2+9$
Or, $p\left(2\right)=4\times 8-7\times 4+10+9$
$\Rightarrow p\left(2\right)=32-28+10+9$
$\therefore p\left(2\right)=23$.

Find $p\left(0\right)$, $p\left(1\right)$ and $p(-2)$ for the following polynomials
(i) $p\left(x\right)=10x-4x^2-3$ (ii) $p\left(y\right)=(y+2)(y-2)$

(i) given, polynomial is
$p\left(x\right)=10-4x^2-3$
On putting $x=0,1\text{and}-2$ respectivel,y in Eq .(i) we get
$p\left(o\right)=0\left(0\right)-4{\left(0\right)}^2-3$
$=0-0-3=-3$
$p\left(1\right)=10\left(1\right)-4{\left(1\right)}^2-3$
$=10-4-3=10-7=3$
$\text{and}p(-2)=10(-2)-4{(-2)}^2-3$
$=-20-4\times 4-3$
$=-20-16-3=-39$
Hence , the values of $p\left(0\right),p\left(1\right)\text{and}p(-2)$ are respecively ,$-3,3\text{and}-39.$
(ii) Given ,polynomial is $p\left(y\right)=(y+2)(y-2)$
On putting $y=0,1\text{and}-2$, respectively in Eq,(i) , we get
$p\left(0\right)=(0+2)(0-2)=-4$
$p\left(1\right)=(1+2)(1-2)$
$=3\times (-1)=-3$
and $p(-2)=(-2+2)(-2-2)$
$=0(-4)=0$
Hence, the values of $p\left(0\right),p\left(1\right)\text{and}p(-2)$ respecively, $-4,-3\text{and}0$.

If we have a polynomial, $p\left(x\right)$then $x$ ki wo value jo hame $p\left(x\right)=0$ deti hai, then that value of $x$ is nothing but the Zero of the Polynomial.

Find the zeroes of the polynomial in each of the following.
$\left(i\right)p\left(x\right)=x-4$ $\left(ii\right)g\left(x\right)=3-6x$
$\left(iii\right)q\left(x\right)=2x-7$ $\left(iv\right)h\left(y\right)=2y$

(i) Given polynomial is
$p\left(x\right)=x-4$
For zero of polynomial, put $p\left(x\right)=0$
$\therefore$ $x-4=0$
$\Rightarrow$ $x=4$
(ii) Given, polynomial is
$g\left(x\right)=3-6x$
For zero of polynomial, put $g\left(x\right)=0$
$3-6x=0\Rightarrow 6x=3$
$\Rightarrow x=\frac{3}{6}=\frac{1}{2}$
Hence, zero of polynomial is$.\frac{1}{2}.$
(iii) Given, polynomial is $q\left(x\right)=2x-7$
For zero polynomial, put $q\left(x\right)-0$
$\therefore$ $2x-7=0$
$\Rightarrow 2x=7\Rightarrow x=\frac{7}{2}$
Hence , zero of polynomial is $\frac{7}{2}$
(iv) Given polynomial is $h\left(y\right)=2y$
For zero of polynomial ,. put $h\left(y\right)=0$
$\therefore 2y=0\Rightarrow y=0$
Hence the zero of polynomial is 0.

Find the zeroes of the polynomial$p\left(x\right)={(x-2)}^2-{(x+2)}^2$.

Given,polynomial is $p\left(x\right)={(x-2)}^2-{(x+2)}^2$
For zeroes of polynomial, put $p\left(x\right)=0$
therefore ${(x-2)}^2-{(x+2)}^2=0$
$\Rightarrow (x-2+x+2)(x-2-x-2)=0[\text{using identity}{a}^2-b^2=(a-b)(a+b)]$
$\Rightarrow \left(2x\right)(-4)=0$
$\Rightarrow -8x=0$
$\Rightarrow x=0[-8\ne 0]$
Hence, zero of the polynomial p(X) is 0.

Jaisa ki hum jante hai if we divide a number for example 5 with 3, we will have remainder $=2$ and Quotient $=1$.
Here we can write $5=3\times 1+2$
In other words (Dividend)= (Divisor) $\times$ (Quotient) $+$ (Remainder)
Where
Dividend = 5
Divisor = 3
Remainder = 2
Quotent = 1
Ek baat ka frnds hmesha dhyan rkhenge ki if we are getting remainder = 0.
Which means divisor, ne dividend ko pura pura divide kr diya in that case divisor is nothing but a factor of the dividend.
To kya hme har bar remainder get karne ke liye pura pura divide krna padega?
Actually hum aisa kar sakte hai but we have Remainder Theorem, jo ise or bhi aasan bna deti hai.
Acording to Remainder Theorem agar kise polynomial ko, suppose $p\left(x\right)$, jiski degree one ya one se zayada hai, $g\left(x\right)=(x-a)$ se divide karte hai to Remainder will be $p\left(a\right)$.
Where $a$ is any real number.
Matlab, ksie Polynomial $p\left(x\right)$ ko kise dusre polynomial $g\left(x\right)=x-a$ se divide karna ho to remainder get karne ke liye put $g\left(x\right)=0$.
$\therefore$$x-a=0$
=> $x=a$
Now find $p\left(a\right)$, then the result will be remainder.

Let $f\left(x\right)$ is divided by $g\left(x\right)=ax+b$ and the quotient is $q\left(x\right)$ as well as the remainder is R.
Well in that case we can write :
$f\left(x\right)=q\left(x\right)g\left(x\right)+R$.
Or, $f\left(x\right)=q\left(x\right)(ax+b)+R$
Now, we have $g\left(x\right)=ax+b$
$\Rightarrow x=-\frac{b}{a}$
Now, putting value of $x$ in $f\left(x\right)$
We get $f(-\frac{b}{a})=q(-\frac{b}{a})(a\times -\frac{b}{a}+b)+R$
$\Rightarrow f(-\frac{b}{a})=q(-\frac{b}{a})\times 0+R$
$\Rightarrow f(-\frac{b}{a})=R$

By remainder theorem, find the remainder when $p\left(x\right)$ is divided by $g\left(x\right)$
(i) $p\left(x\right)$ $=x^3-2x^2-4x-1,g\left(x\right)=x+1$
(ii) $p\left(x\right)=x^3-3x^2+4x+50,g\left(x\right)=x-3$

(i) Given $p\left(x\right)=x^3-2x^2-4x-1\text{and}g\left(x\right)=x+1$
Here, zero of $g\left(x\right)$ is $-1$.
When we divide $p\left(x\right)$ by $g\left(x\right)$ using remainder theorem, we get the remainder i.e. $p(-1)$.
$\therefore p(-1)={(-1)}^3-2{(-1)}^2-4(-1)-1$
$=-1-2+4-1$
$=4-4=0$
Hence, remainder is 0.
(ii) Given $p\left(x\right)=x^3-3x+4x+50\text{and}g\left(x\right)=x-3$
Here, zero pf $g\left(x\right)$ is $3$.
when we divide $p\left(x\right)$ by $g\left(x\right)$ using remainder theoem, we get the remainder i.e. $p\left(3\right)$.
$\therefore p\left(3\right)={\left(3\right)}^3-3{\left(3\right)}^2+4\left(3\right)+50$
$=27-27+12+50=62$
Hence, remainder is $62$.

If we divide $p\left(x\right)$ with $q\left(x\right)$ and maan lo remainder is $0$, then q(x) is a factor of $p\left(x\right)$.
Similarly iska ulta bhi valid hai
Matlab, Jab $p\left(x\right)$ ko $q\left(x\right)$ se divide karte hain and hme pta hai ki $q\left(x\right)$ is a factor of $p\left(x\right)$ then hum ye keh sakte hai, bina division kiye huye ki, remainder to $0$ hi aayega .

Let $f\left(x\right)$ be a polynomial which is divided by $g\left(x\right)$. This theorem says that if we get the remainder $0$. Then $g\left(x\right)$ is nothing but the factor of $f\left(x\right)$.
Or, we can write $f\left(x\right)=g\left(x\right)\times q\left(x\right)+R$[where $q\left(x\right)$ is quotient and R is reaminder]
So if $g\left(x\right)$ is factor of $f\left(x\right)$ then it can be written as
$f\left(x\right)=g\left(x\right)\times q\left(x\right)+0$
$\Rightarrow f\left(x\right)=g\left(x\right)\times q\left(x\right)$
Chalo kuch examples ki help se is concept ko samajhte hai

Show that
(i) $x+3$ is factor of $69+11x-x^2+x^3$
(ii) $2x-3$ is factor of $x+2x^3-9x^2+12$

(i) Let $p\left(x\right)=x^3-x^2+11x+69$
we have to show that, $x+3$ is a factor of $p\left(x\right)$ .
$i.e.,p(-3)=0$
Now, $p(-3)={(-3)}^3-{(-3)}^2+11(-3)+69$
$=-27-9-33+69=-69+69=0$
Hence, $(x+3)$ is a factor of $p\left(x\right)$ .
(ii) Let $p\left(x\right)=2x^3-9x^2+x+12$
we have to show that, $2x-3$ is a factor of $p\left(x\right).$
i.e., $p\left(\frac{3}{2}\right)=0$
Now, $p\left(\frac{3}{2}\right)=2{\left(\frac{3}{2}\right)}^3-9{\left(\frac{3}{2}\right)}^2+\frac{3}{2}+12$
$=2\times \frac{27}{8}-9\times \frac{9}{4}+\frac{3}{2}+12$
$=\frac{27}{4}-\frac{81}{4}+\frac{3}{2}+12$
$=\frac{27-81+6+48}{4}=\frac{81-81}{4}=0$
Hence, $(2x-3)$ is a factor of $p\left(x\right)$.

Man lo, we have a Quadratic Polynomial equation which is written in the form $a{x}^2+bx+c=0$
Where $a$ = coefficient of $x^2$.
$b$ = coefficient of $x$.
$c$ = a constant.
to iske factorization find krne ka matlab hoga ki polynomial ko aise multiples ke form me likhna jo us polynomial ke factor ho.
Let $a{x}^2+bx+c=0$
Step 1 : Break the middle term $(+bx)$ as $l$ and $m$, such that.
$l+m=(+bx)$
and $l\times m=a{x}^2\times c$
Step 2 : Now we will have four terms in which we have to take common from first two and second two terms.
Step 3:Take final common terms and humare pas required factors honge.
Chalo example se samjhte hai.

Factorise the following :
(i) $9x^2-12x+3$ (ii) $9x^2-12x+4$

(i) $9x^2-12x+3=3(3x^2-4x+1)$ [taking 3 common factor ]
$=3(3x^2-3x-x+1)$ [by splitting middle term]
$=3[3x(x-1)-1(x-1)]=3(3x-1)(x-1)$
(ii) $9x^2-12x+4={\left(3x\right)}^2-2\times 3\times 2x+{\left(2\right)}^2$
$={(3x-2)}^2$ [ using identity,${(a-b)}^2=a^2-2ab+b^2]$
$=(3x-2)(3x-2)$

Factorise
(i) $x^2+9x+18$ (ii) $6x^2+7x-3$
(iii) $2x^2-7x-15$(iv)$84-2r-2r^2$

(i) $x^2+9x+18=x^2+6x+3x+18$ [by splitting middle term]
$=x(x+6)+3(x+6)=(x+3)(x+6)$
(ii) $6x^2+7x-3=6x^2+9x-2x-3$ [by splitting middle term]
$=3x(2x+3)-1(2x+3)$ $=(3x-1)(2x+3)$
(iii) $2x^2-7x-15=2x^2-10x+3x-15$ [by splitting middle term]
$=2x(x-5)+3(x-5)=(2x+3)(x-5)$
(iv) $84-2r-2r^2=-2(r^2+r-42)$
$=-2(r^2+7r-6r-42)$ [by splitting middle term]
$=-2[r(r+7)-6(r+7)]$
$=-2(r-6)(r+7)=2(6-r)(r+7)$

Is pure chapter me hume total 10 identities ke bare me padhna hai jisme se kuch ke bare hum pehle se hi jante hai and kuch identities hmare liye bilkul naye hai aaiye pehle unhe jante hai or fir sabko examples se samjhne ki koshis krenge.
i. ${(x+y)}^2=x^2+2xy+y^2$
ii. ${(x-y)}^2=x^2-2xy+y^2$
iii. $(x+a)(x+b)=x^2+(a+b)x+ab$
iv. $x^2-y^2=(x+y)(x-y)$
v. ${(x+y+z)}^2=x^2+y^2+z^2+2xy+2yz+2xz$
vi. ${(x+y)}^3=x^3+y^3+3xy(x+y)$
$\text{or},{(x+y)}^3=x^3+y^3+3x^{2}y+3x{y}^2$
vii. ${(x-y)}^3=x^3-y^3-3xy(x-y)$
$\text{or}{(x-y)}^3=x^3-y^3-3x^{2}y+3x{y}^2$
viii. $x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-xz)$
ix. $x^3+y^3=(x+y)(x^2-xy+y^2)$
x. $x^3-y^3=(x-y)(x^2+xy+y^2)$