HERON'S FORMULA for Class 9 MATHS

Baccho, aapne apni previous classes m alag alag shapes k baare m pdha hai jaise ki squares, rectangles, triangles, circles, etc. Humne saath m hi inn sabhi shapes ki properties k baare m bhi seekha aur ye bhi jaana ki inke areas and perimeters kaise find kiye jaate hai. Imagine kro ki aap ek rectangular park m hai. Jab aap iss park k around ghumenge to aap basically uss park ka perimeter cover krrhe honge. Similarly, agar suppose ki aapko uss pure park ki grass ko water krna hai to aap uska area cover krenge. Also we can recall that unit of measurement for length or breadth is taken as metre $\left(m\right)$ or centimetre $\left(cm\right)$ etc. Unit of measurement for area of any plane figure is taken as square metre $\left(m^2\right)$ or square centimeter $\left(c{m}^2\right)$ etc.
Baccho, iss chapter m hum triangles se deal krenge. We'll learn about a new method to calculate the area of a triangle which is known as the heron's formula aur fir hum dekhenge ki hum apni day to day life m iss method ko konsi situations m apply kr skte hai. So let's get started!

Baccho before learning the heron's method of calculating the area of a triangle, hum phle triangle se related previous formulas revise krlete hai.

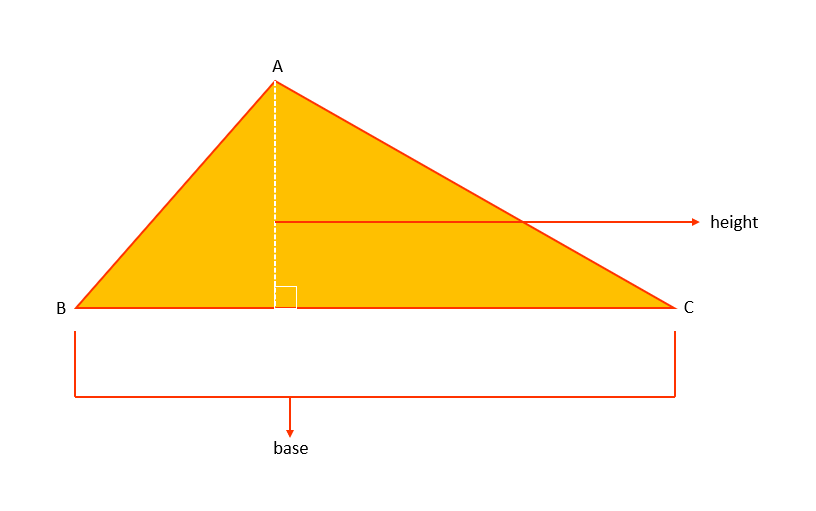
Baccho suppose ki aapke paas ek triangular floor mat hai, aap uska area kaise calculate krenge? We have learnt in our previous classes that :
$\text{AREA OF A TRIANGLE}$ $=\frac{1}{2}\times \text{BASE}\times \text{HEIGHT}$
Base is the side of the triangle on which it stands.
Height refers to the perpendicular from the corner of the triangle to the base of the triangle.
Let's say ki jo given diagram hai vo humare floor mat hai and we need to find its area.

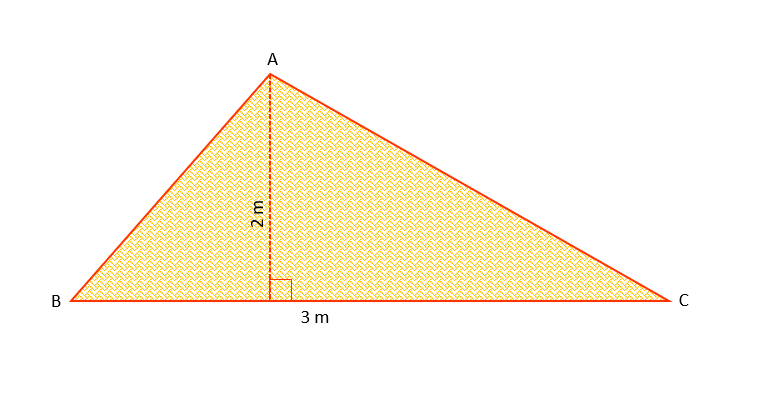
Baccho jaisa ki aap dekh skte hai figure m se:
Base $=$ $3$ $m$
Height $=$ $2$ $m$
Jab hum iss situation m area of a triangle ka formula apply krenge then we'll get:
Area of the mat $=\frac{1}{2}\times 3\times 2$
$\Rightarrow$Area $=3$ $m^2$

Baccho, abhi tak humne seekha ki hum ek triangle ka area kaise calculate krte hai jab hume uske base ki aur height ki dimensions given ho. But what if agar hume sirf triangle ki sides given ho without the dimension of the height?
For this we'll learn about the Heron's formula
Heron's formula or Hero's formula is stated as:
Area of a triangle $=$ $\sqrt{s(s-a)\times (s-b)\times (s-c)}$
where $a,b$ and $c$ are the sides of the triangle, and $s=$ semi-perimeter, i.e., half the perimeter of the triangle $=\frac{a+b+c}{2}$
Let's understand how to use this formula with an example:
In a triangle $ABC$,
$AB=a=40m$
$BC=b=24m$
$BC=c=32m$
$\Rightarrow s=\frac{a+b+c}{2}$
$\Rightarrow s=\frac{40+24+32}{2}$ $m=48m.$
$s-a=(48–40)m=8m$,
$s-b=(48–24)m=24m$,
$s-c=(48–32)m=16m.$
$\therefore Area=$$\sqrt{s(s-a)\times (s-b)\times (s-c)}$
$\Rightarrow \sqrt{48\times 8\times 24\times 16}{m}^2=384m^2$

A triangular park $ABC$ has sides $120m,80m$ and $50m$. A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of $Rs.20$ per meter leaving a space $3m$ wide for a gate on one side.

Length of fence=perimeter of Triangle-$3m$
$=50+80+120-3$
$=247m$
Cost of wire=length$\times$cost
$=247\times 20$
$=Rs.4940$
Herons formula
area=$\sqrt{s(s-a)(s-b)(s-c)}$
=$\sqrt{125(125-120)(125-80)(125-50)}$
=$375\sqrt{15}{m}^2$

The sides of a triangular plot are in the ratio of $3:5:7$and its perimeteris $300m$. Find its area.

$a:b:c=3:5:7$
$a=3x=60$
$b=5x=100$
$c=7x=140$
$a+b+c=300$
$3x+5x+7x=300$
$15x=300$
$x=20$
Semi-perimeter$=\frac{300}{2}=150$
Herons formula
area=$\sqrt{s(s-a)(s-b)(s-c)}$
=$\sqrt{150(150-60)(150-100)(150-140)}$
=$1500\sqrt{3}{m}^2$

For a quadrilateral, when one of its diagonal value and the sides are given, the area can be calculated by splitting the given quadrilateral into two triangles and use the Heron’s formula.
Example :A park, in the shape of a quadrilateral $ABCD$, has $\angle C={90}^{\circ },AB=9cm,BC=12cm,CD=5cm$ and $AD=8cm$. How much area does it occupy?

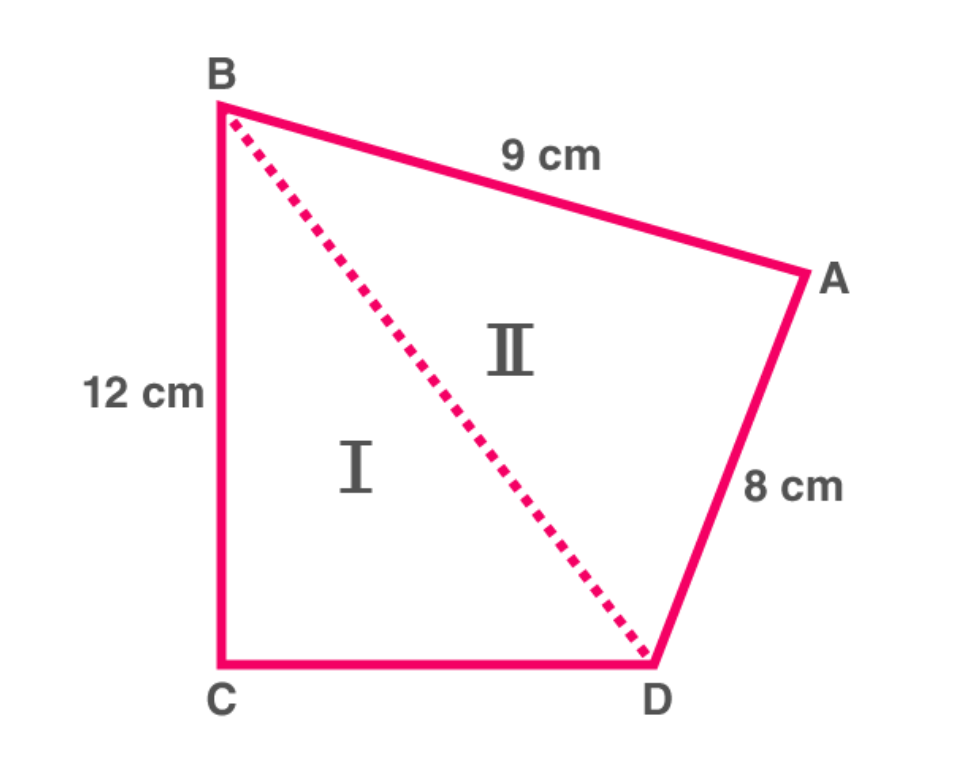
The figure can be split into $2$ triangles $△BCD$ and $△ABD$
From $△BCD$, we can find $BD$ (Using Pythagoras’ Theorem)
$B{D}^2=122+52=169$
$BD=13cm$
Semi-perimeter for $△BCD$
$S1=\frac{12+5+13}{2}=15$
Semi-perimeter $△ABD$
$S2=\frac{9+8+13}{2}=15$
Using Heron’s formula $A1$ and $A2$ will be:
$A1=\sqrt{15(15–12)(15–5)(15–13)}$
$A1=\sqrt{15\times 3\times 10\times 2}$
$A1=\sqrt{900}=30c{m}^2$
Similarly,
$A2$ will be $35.49c{m}^2$.
The area of the quadrilateral $ABCD=A1+A2=65.49c{m}^2$
This is how we can use heron's formula to calculate the area of other polygons as well.

Baccho ab hum dekhenge ki hum apni day to day life m heron's formula ko kaha aur kaise apply krte hai. Let's take an example to understand it:
Students of a school staged a rally for cleanliness campaign. They walked through the lanes in two groups. One group walked through the lanes $AB$, $BC$ and $CA$; while the other through $AC$, $CD$ and $DA$

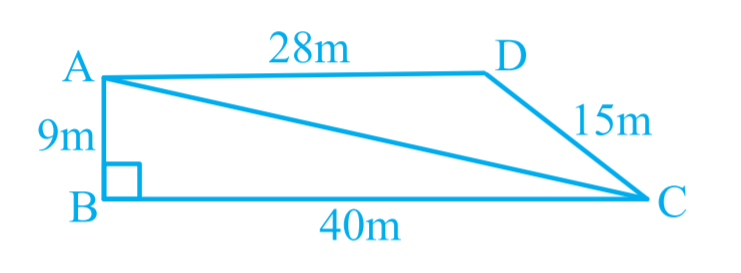
Then they cleaned the area enclosed within their lanes. If $AB=9m$, $BC=40m$, $CD=15m$, $DA=28m$ and $\angle B={90}^{\circ }$, which group cleaned more area and by how much? Find the total area cleaned by the students (neglecting the width of the lanes).
Baccho hum question pdhke ye smjh skte hai ki humare paas ek four sided figure hai jo ki ek diagonal se divided hai. Therefore, we get two different triangles. Kyunki humara first triangle ek right angled triangle hai aur hume uski height pta hai to hum uska area bina heron's formula k calculate krlenge and using pythagoras we'll calculate the hypotenuse of this triangle which is also the third side of our second triangle. Baccho jab hume humare second triangle ki third side pta chl jaaegi uske baad hum heron's formula apply krke uska bhi area nikaal lenge and dono areas ko compare krlenge.
Since $AB=9m$ and $BC=40m$, $\angle B={90}^{\circ }$, we have:
$AC=\sqrt{9^2+{40}^2}$$m$
$=\sqrt{81+1600}m$
$=\sqrt{1681}m$
$=41m$
Therefore, the first group has to clean the area of triangle $ABC$, which is right angled.
Area of $△ABC=\frac{1}{2}\times \text{base}\times \text{height}$
$=\frac{1}{2}\times 40\times 9m^2$
$=180m^2$
The second group has to clean the area of triangle $ACD$, which is scalene having sides $41m,15m$ and $28m.$
We'll start by calculating the semi-perimeter:
$s=\frac{41+15+28}{2}$ $m$
$=42m$
Therefore, area of $△ACD=$$\sqrt{s(s-a)\times (s-b)\times (s-c)}$
$=\sqrt{42(42-41)(42-15)(42-28)}$ $m^2$
$=\sqrt{42\times 1\times 27\times 14}$$m^2$
$=126m^2$
So first group cleaned $180m^2$ which is $(180–126)m^2$ , i.e., $54m^2$ more than the area cleaned by the second group.
Total area cleaned by all the students $=(180+126)m^2$
$=306m^2$

Sanya has a piece of land which is in the shape of a rhombus. She wants her one daughter and one son to work on the land and produce different crops to suffice the needs of their family. She divided the land in two equals parts. If the perimeter of the land is $400m$ and one of the diagonals is $160m,$how much area each of them will get?

Let $ABCD$ be the field.
Perimeter $=400m$
So, each side $=400m÷4=100m.$
i.e. $AB=AD=100m.$
Let diagonal $BD=160m$.
Then semi-perimeter s of $△ABD$ is given by $s=\frac{100+100+160}{2}$ $m$
$=180m$
Therefore, area of $△ABD=\sqrt{180(180-100)(180-100)(180-160)}$
$=\sqrt{180\times 80\times 80\times 20}$ $m^2$
$=4800m^2$
Therefore, each of them will get an area of $4800m^2$.

A kite in the shape of a square with a diagonal $32cm$ and an isosceles triangle of base $8cm$ and sides $6cm$ each is to be made of three different shades as shown in Figure . How much paper of each shade has been used in it ?

Area$\left(1\right)$ = Area$\left(2\right)$$=\frac{1}{2}\times \text{Area(square)}$ $=\frac{512}{2}=256c{m}^2$
diagonal $=\sqrt{2}\cdot$side
side = $\frac{32}{\sqrt{2}}$
area(square) =${\left(\frac{32}{\sqrt{2}}\right)}^2=512c{m}^2$
$s=\frac{a+b+c}{2}=\frac{6+6+8}{2}=10cm$
heron$\text{'}$s formula for Area$\left(3\right)$ $=\sqrt{s(s-a)(s-b)(s-c)}$
$=\sqrt{10(10-6)(10-6)(10-8)}$
$=\sqrt{2\times 6\times 4\times 4\times 2}$
$=2\times 4\sqrt{5}=8\sqrt{5}c{m}^2$

A field is in the shape of a trapezium whose parallel sides are $25m$ and $10m$. If its non-parallel sides are $14m$ and $13m$, find its area.

$ADBE$ is a parallelogram
$AB=DE$
$AD=BE$
$EC=25-BE=15$
value of $s$ for $△DEC=\frac{13+14+15}{2}=21$
area = $\sqrt{s(s-a)(s-b)(s-c)}$
$=\sqrt{21\cdot 8\cdot 7\cdot 6}$
$=7\cdot 3\cdot 2^2$
$=84uni{t}^2$
$EX=\frac{13}{13+14}\cdot 15$
$=\frac{65}{9}$
Now, $y^2={13}^2-{\left(\frac{65}{9}\right)}^2$
$y=10.8$
total area= $108+84$
$=192uni{t}^2$

In this chapter, you have studied the following points :
$1.$ Area of a triangle with its sides as $a,b$ and $c$ is calculated by using Heron’s formula, stated as:
Area of a triangle $=$ $\sqrt{s(s-a)\times (s-b)\times (s-c)}$
where, $s=\frac{a+b+c}{2}$
$2.$ Area of a quadrilateral whose sides and one diagonal are given, can be calculated by dividing the quadrilateral into two triangles and using the Heron’s formula.