COORDINATE GEOMETRY for Class 9 MATHS

INTRODUCTION

So guys jaisa ki humne number line ke bare me pehle ki classes me pdha hai or kise bhi point ko hum number line par represent karna jante hain. Hum Geometry bhi pehle se hi padhte aa rhe hai, 'Geo' ka matlab hota hai 'Shape' and 'metry' ka matlab hota hai 'measurement'. Toh previous classes me humne different different shapes and unke measuremnet ke bare padh chuke hai like Triangle, Rectangle, Square, etc.
To friends, how coordinate geometry is different ?
Coordinate ka matlab hota hai 'address'. Ab humare mind me ye question aana chaiye ki aap kis ke address ki baat kr rhe ho?
To guys jaisa ki aap sab jante hain koi bhi shape jo hum construct krte hai that is made up of thousands of points right! Is chapter me hum kise point ke address or position or coordinate ke bare detail me janenge sath hi hum padhne wale hai about Cartesian plane , Coordinate of any point on Cartesian plane , How to represent any point on cartesian plane whose coordinate is given etc.

Cartesian System

Jaisa ki hum number line ke bare pehle se jante hai, ab hume us knowledge ko next level pr le jana hai . Yha hum cartesian system ko smjhenge.
Cartesian Plane : Agar hum two number lines ko ek dusre ke perpendicular kise plane pr show krte hai to hume ek two dimensional structure milega that is nothing but our cartesian plane jiski help se hum kise bhi point ki positioning kr sakte hai, ya is cartesian system ko reference maan kr hum kise point ki position ya address bta sakte hai.
Aaiye ise ek example se smjhte hai :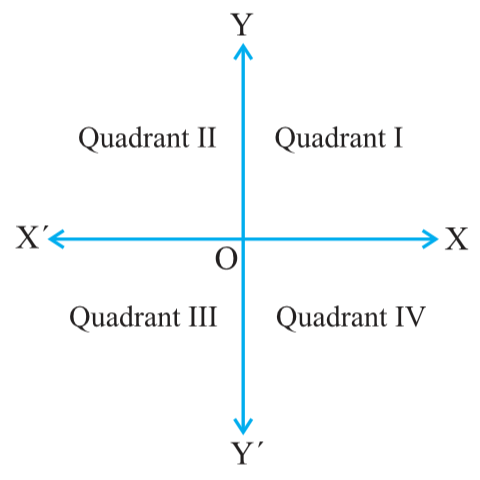
ocr_image
In the above figure Horizontal number line ko $' X -$ axis' kehte hai.
Similarly Vertical number line ko $' Y -$ axis' kehte hai.
Ye dono axis ek dusre ko jis point par cut krte hai us point ko Origin kehte hai.
To guys upar ke fig ko dekh kr or jo bhi humne pdha uske according hum ye keh sakte hai

' O'

is our origin where both number line cut each other.

Horizontal line

X X'

is called

' X -

axis' where

O X

represent 'Positive X-axis' and

O X'

Represents 'Negative X-axis'.

Similarly

Y Y'

is called

' Y -

axis' where

O Y

represents 'Positive Y-axis and

O Y'

represents 'Negative Y-axis '.

Coordinate of a Point

So guys, sabse pehle aao hum quadrants ke bare sikhte hai.
Quadrants : Jaisa ki humne dekha X-axis and Y-axis ek dusre ke Perpendicular to hote hain lakin, dhyan se dekhe to hum ye payenge ki ye dono axes, plane ko four parts me divide bhi kr dete hai jinhe quadrants kehte hai. Jinki naming, Positive X-axis se lete huye anti clock direction me ghumte huye is prakar ki jati hai I, II, III and IV.

The Coordinate of any point is Represented as

P (x, y)

Where

x =

Perpendicular Distance from Y-axis, Which is also called Abscissa.

y =

Perpendicular Distance from X-axis, Which is also known as Ordinate.

Matlab Coordinate

P (x, y)

is basically P(Abscissa, Ordinate).

Sign Convention for Quadrants :

1st quadrant is enclosed by the positive X-axis and the positive Y-axis. So koi bhi Point Jo first Quadrant me hogi that will be in the form of $(+, +)$ . Ex :

P (3, 4)

2nd quadrant is enclosed by the negative X-axis and the positive Y-axis. So point ka form hone wala hai $(-, +)$ . Ex :

P (- 5, 6)

3rd quadrant is enclosed by the negative X-axis and the negative Y-axis. So point ka form hone wala hai

(-, -)

. Ex :

P (- 8, - 7)

4th quadrant is enclosed by the positive X-axis and the negative Y-axis. So Koi bhi point jo 4th quadrant me hogi uska form hoga

(+, -)

. Ex :

P (8, - 9)

Note: Right hand distance from Y-axis, along X-axis is considered as Positive distance and Left hand distance from Y-axis along X-axis is considered as negative.
Similarly X-axis ke upar koi bhi distance jo hum lete hai, along Y-axis, that is considered as positive. And X-axis ke niche koi bhi distance hum travel krte hai to use Negative lete hai.

Example 1

Write down the coordinates of each of the following point A, B, C, D and E.
ocr_image

So guys jaisa ki humare pas ek cartesian plane given hai jisme kuch points hain jinke coordinates hume find out krne hai.
For Point A : Since distance of the point A from the Y-axis is 6 units in left side so x coordinate is (-6) and Point A is 5 units above from the X-axis so y coordinate is (5). Hence we can write the coordinates of A is $(- 6, 5)$ .
For point B: x-cordinate is (5) and y coordinate is (4) so the coordinates of B is $(5, 4)$ .
Q. Similarly kya aap points C, D and E ke coordinates likh sakte ho ?

Learn more

Example 2

If the coordinates of the two points are $P (- 2, 3)$ and $Q (- 3, 5)$ , then (Abscissa of P) $-$ (Abscissa of Q) is.

We have, points $P (- 2, 3)$ and $Q (- 3, 5)$
Here, abscissa of P i.e., x-coordinate of P is $- 2$ and abscissa of Q i.e., x-coordinate of Q is $- 3$ So, (Abscissa of P) $-$ (Abscissa of Q) $= - 2 - (- 3) = - 2 + 3 = 1$ .

Learn more

Plotting a Point in the Plane if its Coordinates are Given

Man lo aapke pas koi point P(3,4) given hai and aapko ise cartesian plane pr plot krne ko kha jata hai.
Well in that case we will follow some steps.
Step 1 : Aap sabse pehle to ek Cartesian plane draw kroge jaisa ki humne dekha hai pehle. We have to draw X - axis and Y - axis.
Step 2 : Ab bari aati hai Unit distance lene ki, to guys aap ise apne according choose kr sakte hai. Kise ke liye1cm ki distance 1 unit hogi to kise or ke liye 5cm distance one unit hogi to apne according aap unit decide kr lenge then aap X and Y axis ko equal units me divide kr lenge.
Step 3 : Now P(3,4) ka matlab hai x-coordinate is 3 and y-coordinate is 4.
Starting from origin we count 3 units in positive x axis and draw a dotted line parallel to Y- axis
Step 4 : Similarly starting from origin count 4 units in positive Y-axis and draw a dotted line parallel to X-axis.
Step 5 : The point where both dotted lines will meet that will be our required point.

Example 3

The three vertices of a $△ A B C$ are $A (1, 4), B (- 2, 2) and C (3, 2)$ . Plot these points on a graph paper and calculate the area of $△ A B C$ .

Let X'OX and YOY' be the x-axis and the y-axis respectively, drawn on graph paper.
Let $A (1, 4), B (- 2, 2) and C (3, 2)$ be the vertices of $△ A B C$ .
Draw $A L ⊥ X' O X$ , meeting BC at M
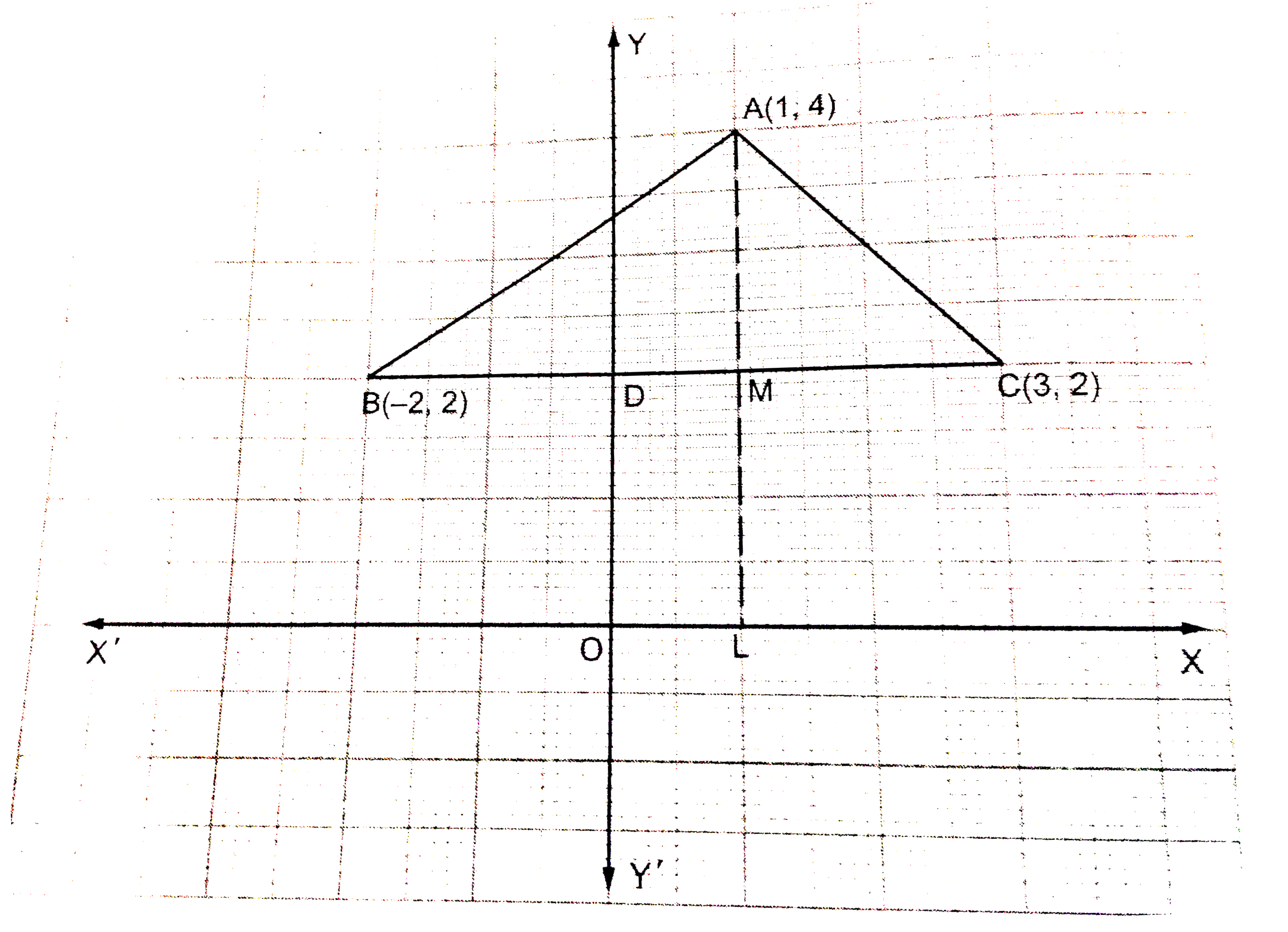
ocr_image
$B C = (B D + D C) = (2 + 3)$ units = 5 units
$A M = (A L - L M) = (4 - 2)$ units = 2 units.
$∴ a r (△ A B C) = (\frac{1}{2} \times B C \times A M) s q$ units
$= (\frac{1}{2} \times 5 \times 2)$ sq units = 5 sq units.

Learn more

Summary

So guys, es chapter me humne sikha :
(i) Cartesian plane ki help se kise bhi point ki position bta sakte sakte hai sath hi sath hum kise point ko cartesian plane ki help se plot bhi kar sakte hai.
(ii) In cartesian plane we have two perpendicular lines jisme horizontal line ko X-axis kehte hai hain and vertical line ko Y-axis kehte hai. Or ye lines or kuch nahi balki Number lines hai jiske bare hum sab padh chuke hai.
(iii) Cartesian plane ko hi Coordinate plane bhi kehte hai. Jo ek two dimensional plane hai. And perpendicular lines are called axes.
(iv) Axes Cartesian plane ko four parts me divide kr deta hai jinhe quadrant kehte hain.
(v) The point of intersection of axes is called origin.
(vi) The distance of a point from the origin is called its x-coordinate, or abscissa, and the distance of the point from the origin is called its y-coordinate, or ordinate.
(vii) If the abscissa of a point is x and the ordinate is y, then (x, y) are called the coordinates of the point.
(viii) Agar koi point X-axis pe hai then its coordinate will be $(x, 0)$ similarly if a point exist on Y-axis then its coordinate will be $(0, y)$ .
(ix) The coordinates of a point are of the form $(+, +)$ in the first quadrant, $(-, +)$ in the second quadrant, $(-, -)$ in the third quadrant and $(+, -)$ in the fourth quadrant, where + denotes a positive real number and – denotes a negative real number.

Let's Revise

Cartesian plane : Cartesian plane is made up of Two Number lines Perpendicular to each other.
ocr_image

The Horizontal number line is called X-axis and the Vertical number line is called Y-axis.

The Point of Intersection of two Axes is called Origin.

Origin, X-axis ko Two parts me divide karta hai. If we take a distance Right to the origin along X-axis, that is positive. Similarly if we travel a distance to the left of the origin along X-axis that will be negative.

Origin, Y-axis ko Two parts me divide kr deta hai. If we take a distance in upward direction from the origin along Y-axis, that will be positive. Similarly the distance travelled below the origin along Y-axis is taken as negative.

Axes divides the plane in exactly four parts which called Quadrants and named as I, II, III, and IV. In anti-clock wise direction. See fig below :

The Coordinate of any point is represents as

(x, y)

Where

x

represents the perpendicular distance of a point from Y-axis also known as Abscissa.

y

represents the perpendicular distance of a point from X-axis known as Ordinate.

Koi bhi point, which exist in first quadrant will be of the form of

(+, +)

. Similarly point in the second quadrant will be of the form of

(-, +) .

And any point that lies on the third quadrant will be of the form

(-, -)

and any point lies in the fourth quadrant will be of the form of

(+, -)

For plotting a point with the help of Cartesian plane we need a Graph paper on which we draw X-axis and Y-axis. Iske bad hume axes ko chote chote equal parts me divide kerna hota hai. Jise unit distance kehte hai jo hum apne according kuch bhi man sakte hai like 1cm or 2cm or 5cm etc.
Iske bad hum abscissa and ordinate ke according, with respect to origin, unit distance measure krte huye dotted lines draw krte hai. For abscissa dotted line will be parallel with Y-axis and for ordinate the dotted line will be parallel with X-axis.

The point of intersection of both dotted lines will be our required point. See in the figure below:
ocr_image