CONSTRUCTIONS for Class 9 MATHS

Hello bachcho, aapne abhtak bahot sare diagrams, figures banaye hoge kisi theorem ko proof karne ya exercise ko solve karne ke liye par wo ekdum accurate nahi the wo to bas aapko situation ko feel karane ke liye banate the aur aapko ek proper reasoning dene ke liye. But kabhi kabhi hume ekdum accurate figure ya diagram ki zarurat hoti hai, for example :- to draw a map of a building to be constructed, to design tools, and various parts of a machine, to draw road maps etc. To inn sab figures ko draw karne ke liye aapko kuch basic geometrical instruments ki zarurat padegi. Toh aapke geometry box mai kuch important aur basic tools hone chahiye, for example :-
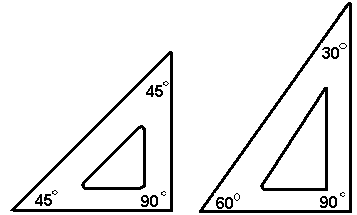
(i) Ek graduated scale yani ki jiske ek side par clearly centimetres and millimetres mark ho aur dusri side par clearly inches and their parts mark ho.

(ii) A pair of set - squares, one with angles ${90}^{\circ }$, ${60}^{\circ }$ and ${30}^{\circ }$ and other with angles ${90}^{\circ }$, ${45}^{\circ }$ and ${45}^{\circ }$.

(iii) A pair of dividers (or a divider) with adjustments.

(iv) A pair of compasses (or a compass) with provision of fitting a pencil at one end.

(v) A protractor

Toh bachcho inn instruments ke saath construction karna shuru karte hai.

Toh bachcho jo instruments humne abhi upar padhe wo normally geometrical figures draw karne ke liye use karte hai jaise ki circle, parallelogram, polygon, etc. But a geometrical construction is the process of drawing a geometrical figure using only two instruments – an ungraduated ruler, also called a straight edge and a compass. Construction mai jaha par measurement ki requirement hoti hai waha par aap graduated scale and protractor use kar sakte hai. Iss chapter mai aapko kuch basic constructions dekhne ko milenge.

Construction in geometry means to draw shapes, angles or lines accurately. These constructions use only compass, straightedge (i.e. ruler) and a pencil.

Aapne Class VI mai circle ko construct karna sikha tha and the perpendicular bisector of a line segment, angles of ${30}^{\circ },{45}^{\circ },{60}^{\circ },{90}^{\circ }$ and ${120}^{\circ }$ and the bisector of a given angle, aap inn constructions ko bina kisi justification ke banate the. Abh aap iss section mai construction karoge but with proper reason and justification that why these constructions are valid.

Construct an angle of ${60}^{\circ }$ using ruler and compasses only Justify your construction.

STEPS OF CONSTRUCTION :-
(i) Draw a ray $OA$.
(ii) With $O$ as centre and a convenient radius, draw an arc, cutting $OA$ at $P$.
(iii) With $P$ as centre and the same radius as above, draw an arc, cutting the previous arc at $Q$.
(iv) Join $OQ$ and produce it to a point $B$.
Then, $\angle AOB$ is the required angle of measure ${60}^{\circ }$.

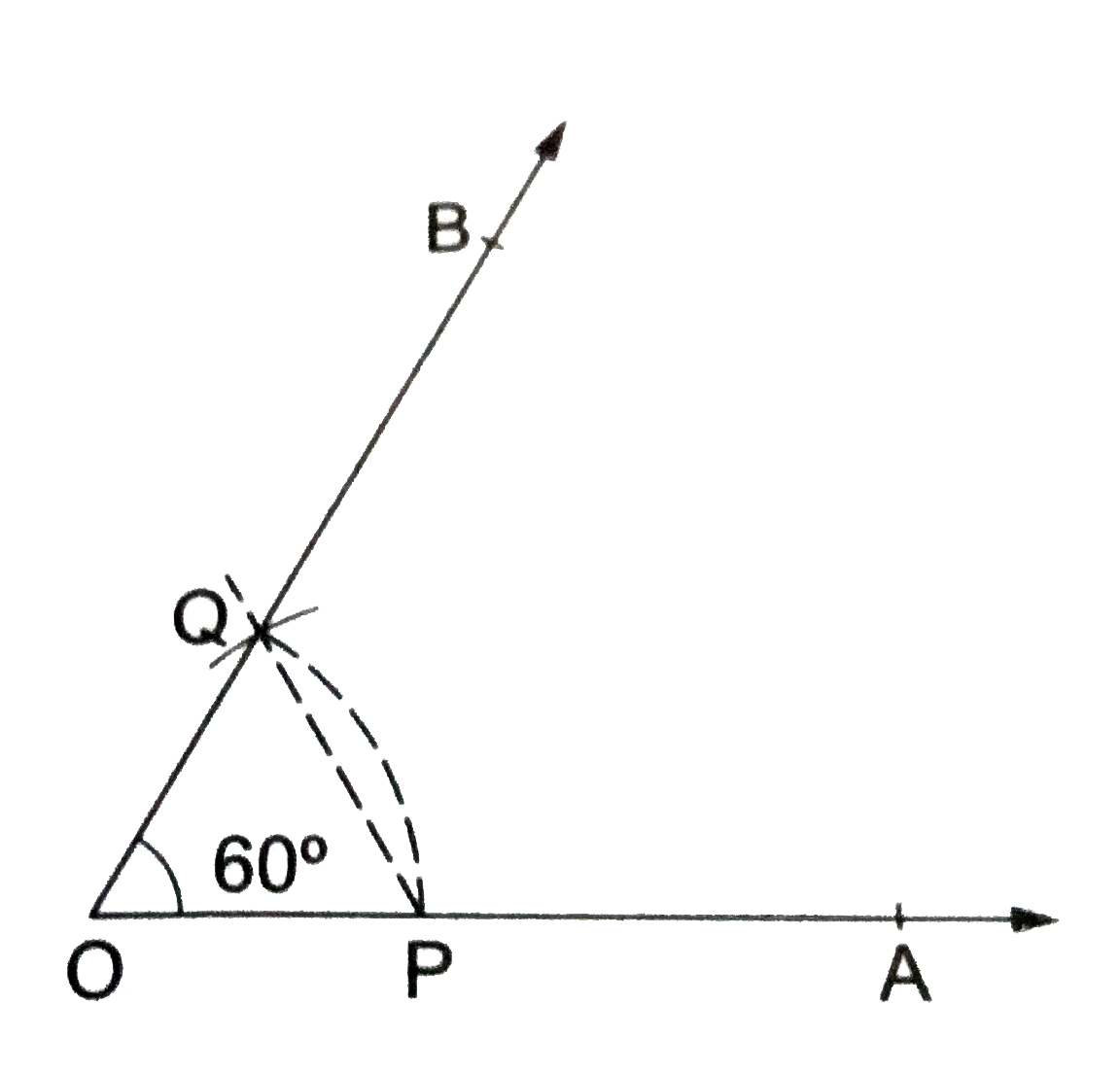
Verification :
If you measure $\angle AOB$ by using a protractor, you will find that $\angle AOB={60}^{\circ }$.
Justification :
Join PQ, as shown in the figure.
Then, $OQ=OP=PQ$ (by construction)
$\therefore \Delta OPQ$ is an equilateral triangle.
Hence, $\angle POQ={60}^{\circ }$ and therefore, $\angle AOB={60}^{\circ }$.

Construct a $\Delta ABC$ in which $BC=6$ cm, $\angle B={60}^{\circ }$ and $(AB+AC)=9$ cm. Measure $AB$ and $AC$. Justify your answer.

STEPS OF CONSTRUCTION
(i) Draw $BC=6$ cm.
(ii) Construct $\angle CBX={60}^{\circ }$.
(iii) Along $BX$, set off $BP=9$ cm.
(iv) Join $CP$.
(v) Draw the perpendicular bisector of $CP$ to intersect $BP$ at $A$.
(vi) Join $AC$.
Then, $\Delta ABC$ is the required triangle.
Verification :
On measuring, we find that
$AB+AC=(4+5)$ cm $=9$ cm.
Justification :
Clearly, $A$ lies on the perpendicular bisector of $CP$.
$\therefore AP=AC$.
Now, $BP=9$ cm [see Step (iii)]
$\Rightarrow AB+AP=9$ cm
$\Rightarrow AB+AC=9cm[\because AP=AC]$.
Hence, $\Delta ABC$ is the required triangle.

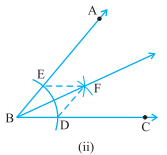
To construct the bisector of a given angle.

Given an angle $ABC$, we want to construct its bisector.
Steps of Construction :
$1$. Taking $B$ as centre and any radius, draw an arc to intersect the rays $BA$ and $BC$, say at $E$ and $D$ respectively. [fig. (i)]

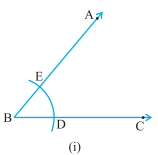
$2$. Next, taking $D$ and $E$ as centres and with the radius more than $\frac{1}{2}$ $DE$, draw arcs to intersect each other, say at $F$.
$3$. Draw the ray $BF$ . This ray $BF$ is the required bisector of the angle $ABC$. [fig. (ii)]

From Construction,
Join $DF$ and $EF$.
In triangles $BEF$ and $BDF$,
$BE=BD$ (Radii of the same arc)
$EF=DF$ (Arcs of equal radii)
$BF=BF$ (Common)
$\therefore$ $\Delta BEF\cong \Delta BDF$ ( $SSS$ rule)
This gives $\angle EBF=\angle DBF\left(CPCT\right)$

To construct the perpendicular bisector of a given line segment.

Given a line segment $AB$, we want to construct its perpendicular bisector.
Steps of Construction :
$1$ . Taking $A$ and $B$ as centres and radius more than $\frac{1}{2}$ $AB$, draw arcs on both sides of the line segment $AB$ (to intersect each other).
$2$. Let these arcs intersect each other at $P$ and $Q$.
Join $PQ$.

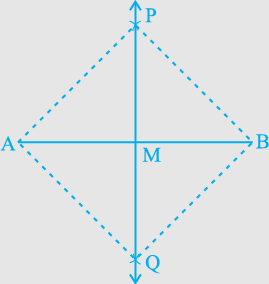
$3$. Let $PQ$ intersect $AB$ at the point $M$. Then line $PMQ$ is the required perpendicular bisector of $AB$.

From Construction,
Join $A$ and $B$ to both $P$ and $Q$ to form $AP$, $AQ$, $BP$ and $BQ$.
In triangles $PAQ$ and $PBQ$,
$AP=BP$ (Arcs of equal radii)
$AQ=BQ$ (Arcs of equal radii)
$PQ=PQ$ (Common)
$\therefore$ $\Delta PAQ\cong \Delta PBQ$ ( $SSS$ rule)
So, $\angle APM=\angle BPM\left(CPCT\right)$
Now in triangles $PMA$ and $PMB$,
$AP=BP$ (As before)
$PM=PM$ (Common)
$\angle APM=\angle BPM$ (Proved above)
$\therefore$ $\Delta PMA\cong \Delta PMB$ ( $SAS$ rule)
So, $AM=BM$ and $\angle PMA=\angle PMB\left(CPCT\right)$
As $\angle PMA+\angle PMB={180}^{\circ }$ (Linear pair axiom),
we get,
$\angle PMA=\angle PMB={90}^{\circ }.$
Therefore, $PM$, that is, $PMQ$ is the perpendicular bisector of $AB$.

To construct an angle of ${60}^{\circ }$ at the initial point of a given ray.

Let us take a ray $AB$ with initial point $A$. We want to construct a ray $AC$ such that $\angle CAB={60}^{\circ }$. One way of doing so is given below.

Steps of Construction :
$1$. Taking $A$ as centre and some radius, draw an arc of a circle, which intersects $AB$, say at a point $D$.
$2$. Taking $D$ as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point $E$.

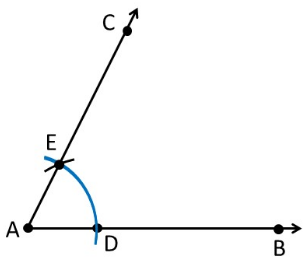
Draw the ray $AC$ passing through $E$. Then $\angle CAB$ is the required angle of ${60}^{\circ }$.

From Construction,
Join $DE$.
Then, $AE=AD=DE$ (By construction)
Therefore, $\Delta EAD$ is an equilateral triangle and the $\angle EAD$, which is the same as $\angle CAB$ is equal to ${60}^{\circ }$.

Abhi tak aapne kuch basic construction dekhe hai. Next, abh hum triangles ki construction dekhenge by using above mentioned instruments. Recall from the Chapter $7$ that $SAS,SSS,ASA$ and $RHS$ rules give the congruency of two triangles. Therefore, a triangle is unique if :
(i) Agar triangle ki koi two side and included angle given ho
(ii) Triangle ki tino side given ho,
(iii) Agar triangle ke two angle and included side given ho,
(iv) In a right triangle, hypotenuse and one side is given.
Aapne already Class VII mai inn triangles ko construct karna sikha tha.
Now, let us consider some more constructions of triangles. Aapne yaha par ek cheej notice ki hogi triangle ko construct karne ke liye hume atleast three parts pata hone chahiye. But not all combinations of three parts are sufficient for the purpose. For example, if two sides and an angle (not the included angle) are given, then it is not always possible to construct such a triangle uniquely.

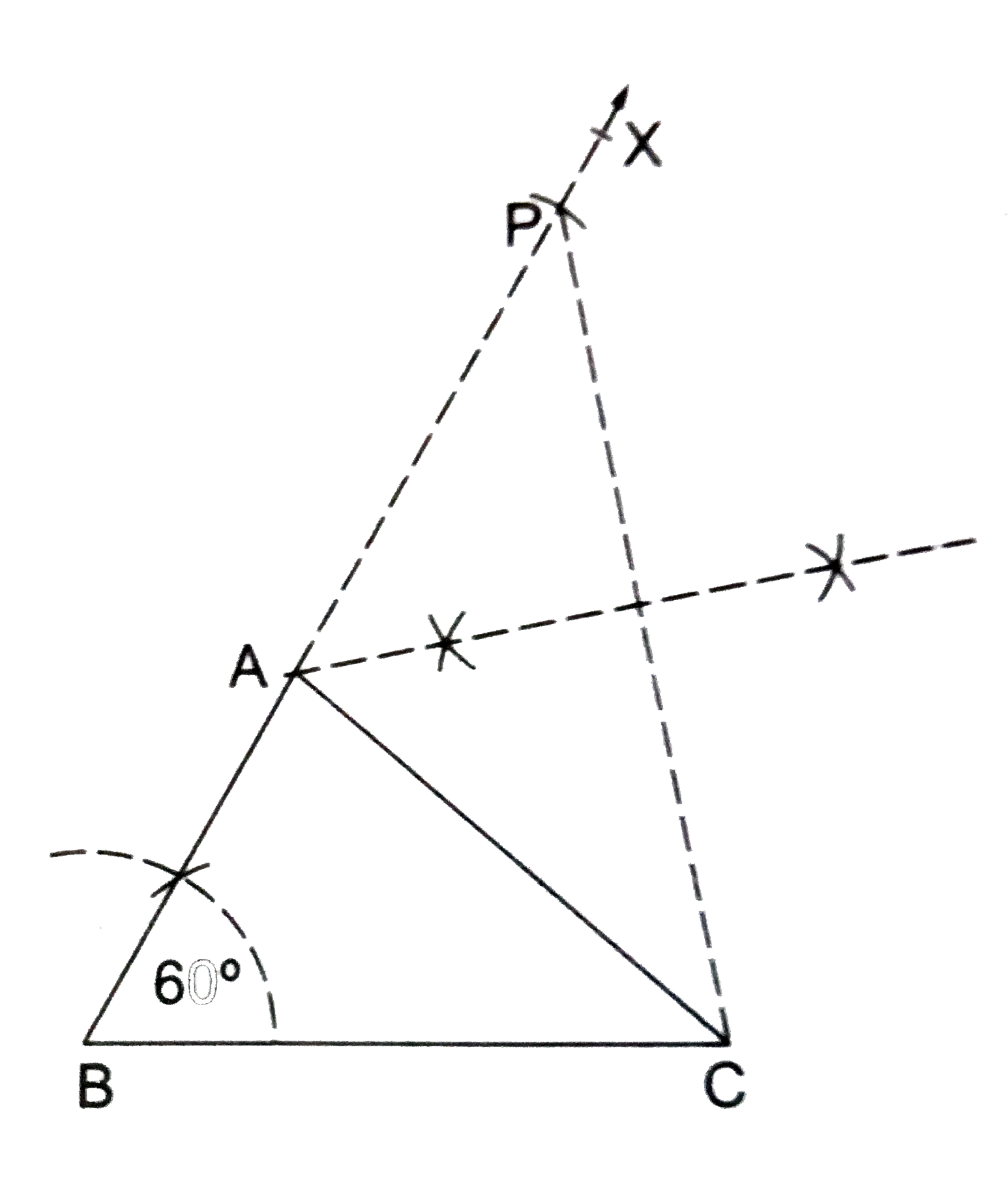
Construct a $\Delta ABC$ whose perimeter is $12cm$ and the base angles are ${60}^{\circ }$ and ${70}^{\circ }$. Justify the construction.

STEPS OF CONSTRUCTION
(i) Draw a line segment $PQ=12$ cm.
(ii) Make $\angle QPR={60}^{\circ }$ and $\angle PQS={70}^{\circ }$.
(iii) Draw the bisectors of $\angle QPR$ and $\angle PQS$ to meet at A.
(iv) Draw the perpendicular bisectors of $PA$ and $QA$ to meet $PQ$ at $B$ and $C$ respectively.
(v) Join $AB$ and $AC$.
Then, $\Delta ABC$ is the required triangle.

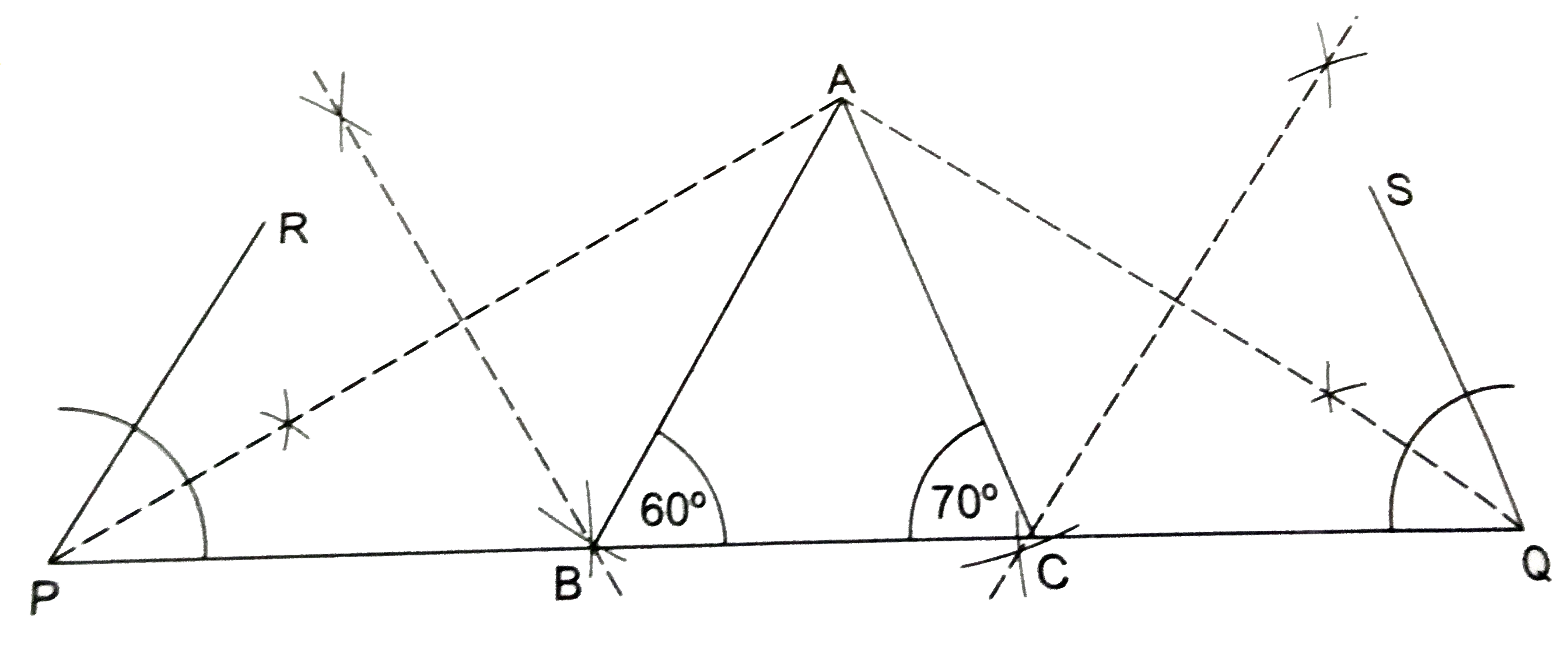
Justification :
Since $B$ lies on the perpendicular bisector of $AP$, we have $BA=BP$. Since $C$ lies on the perpendicular bisector of $AQ$, we have $CA=CQ$. Thus, $AB=PB$ and $AC=CQ$.
$\therefore AB+BC+AC=PB+BC+CQ=PQ=12$ cm.
Now, $BA=BP\Rightarrow \angle BPA=\angle BAP$
$\Rightarrow \angle ABC=\angle BPA+\angle BAP=2\angle BPA$
$=2\times \frac{1}{2}\times {60}^{\circ }={60}^{\circ }$.And, $CA=CQ\Rightarrow \angle CQA=\angle CAQ$
$\Rightarrow \angle ACB=\angle CQA+\angle CAQ=2\angle CQA$
$=2\times \frac{1}{2}\times {70}^{\circ }={70}^{\circ }$.
Verification :
On measurement, we find that
$AB+BC+CA=(4.4+3.5+4.1)cm=12$ cm.
$\angle B={60}^{\circ }$ and $\angle C={70}^{\circ }$.

Construct a $\Delta ABC$ in which base $BC=5.2cm$, $\angle ABC={50}^{\circ }$ and $AB-AC=2cm.$

Steps of construction :
$1.$ Draw $BC=5.3cm.$
$2.$ Construct $\angle PBC={50}^{\circ }$ and cut $BP=2cm.$
$3.$ Join $PC.$
$4.$ Draw the perpendicular bisector of $PC$ which intersect BP produced at $A.$
$5.$ Join $AC.$
$\therefore \Delta ABC$ is the required triangle.

To construct a triangle, given its base, a base angle and sum of other two sides.

Given the base $BC$, a base angle, say $\angle B$ and the sum $AB+AC$ of the other two sides of a triangle $ABC$, we have to construct it.
Steps of Construction :
$1$. Draw the base $BC$ and at the point $B$ make an angle, say $XBC$ equal to the given angle.
$2$. Cut a line segment $BD$ equal to $AB+AC$ from the ray $BX$.
$3$. Join $DC$ and make an angle $DCY$ equal to $\angle BDC$.
$4$. Let $CY$ intersect $BX$ at $A$.

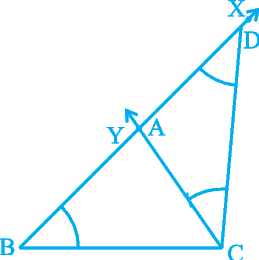
Then, $ABC$ is the required triangle.

From Construction,
Base $BC$ and $\angle B$ are drawn as given. Next in triangle $ACD$,
$\angle ACD=\angle ADC$ (By construction)
Therefore, $AC=AD$ and then
$AB=BD–AD$
$AB=BD–AC$
$AB+AC=BD$

To construct a triangle given its base, a base angle and the difference of the other two sides.

Let $△ABC$ with $\angle B$ and base $BC$ be given.
Now, we are also difference of other two sides.
So, There can be two cases :-
$1.AB>AC$ and difference $AB-AC$ is given.
$2.AC>AB$ and difference AC - AB is given.
Let's do both these cases separately.
Case 1: AB > AC
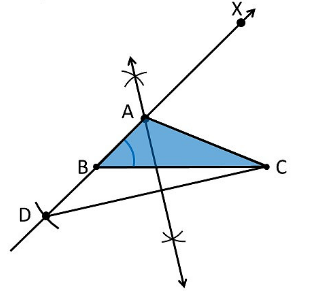
Given the base $BC$, a base angle $\angle B$ and the difference $AB-AC$ we need to construct $△ABC$.
Steps of Construction :
$1.$ Draw base $BC$.
$2.$ Now, let's draw $\angle B$.
Construct angle $B$ from point $B$.
Let the ray be $BX$.
$3.$ Open the compass to length $AB-AC$. [ Since $AB>AC$, (AB - AC) is positive.
So, $BD$ will be above line $BC$ ]
From point $B$ as center, cut an arc on ray $BX$.
Let the arc intersect $BX$ at $D$.
$4.$ Join $CD$.

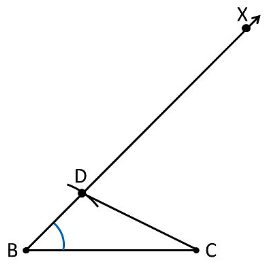
$5.$ Now, we will draw perpendicular bisector of $CD$.
$6.$ Mark point $A$ where perpendicular bisector intersects $BD$.
$7.$ Join $AC$.

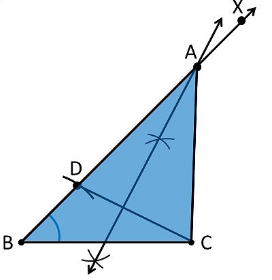
$\therefore △ABC$ s the required triangle.
Case 2 :- $AC>AB$
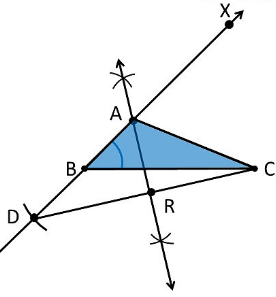
Given the base $BC$, a base angle $\angle B$ and the difference $AC-AB$, we need to construct $△ABC$.
Steps of Construction :
$1.$ Draw base $BC$.
$2.$ Now let's draw $\angle B$
Construct angle $B$ from point $B$.
Let the ray be $BX$.

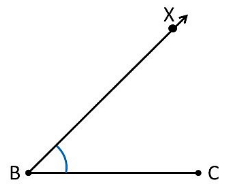
$3.$ Open the compass to length $AC-AB$. [ Since, $AC>AB$ ($AB-AC$) is negative.
So, $BD$ will be below line $BC$ ]
From point $B$ as center, cut an arc on ray $BX$ (opposite side of $BC$ ).
Let the arc intersect $BX$ at $D$.
Join $CD$.
$5.$ Now, we will draw perpendicular bisector of $CD$.
$6.$ Mark point $A$ where perpendicular bisector $BD$.
$7.$ Join $AC$.

$\therefore △ABC$ is required triangle.

Justification Case 1 :-
We need to prove that $AB-AC=BD$.
Let perpendicular bisector intersect $CD$ at point $R$.
Thus,
$AR$ is the perpendicular bisector of $CD$
$\therefore CR=DR......\left(1\right)$
$\angle ARC=\angle ARD={90}^{\circ }.......\left(2\right)$ >
Now,
In $△ADR$ and $△ACR$
$AR=AR$ (common)
$\angle ARD=\angle ARC$ (From ($2$))
$DR=CR$ (From ($1$))
$\therefore △ADR\cong △ACR$ ( $SAS$ Congruency )
$\Rightarrow AC=AD$ $\left(CPCT\right)........\left(3\right)$

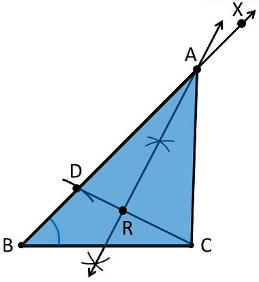
Now,
$BD=AB-AD$
$BD=AB-AC$ (From (3))
Thus, our construction is justified.
Justification Case 2 :-
We need to prove that $AC-AB=BD$.
Let perpendicular bisector intersect $CD$ at point $R$.
Thus,
$AR$ is the perpendicular bisector of $CD$
$\therefore CR=DR......\left(1\right)$
$\angle ARC=\angle ARD={90}^{\circ }.......\left(2\right)$
Now,
In $△ADR$ and $△ACR$
$AR=AR$ (common)
$\angle ARD=\angle ARC$ (From ($2$))
$DR=CR$ (From ($1$))
$\therefore △ADR\cong △ACR$ ( $SAS$ Congruency )
$\Rightarrow AC=AD$ $\left(CPCT\right)........\left(3\right)$

Now,
$BD=AD-AB$
$BD=AC-AB(From($3))
Thus, our construction is justified.

To construct a triangle, given its perimeter and its two base angles.

Given the base angles, say $\angle B$ and $\angle C$ and $BC+CA+AB$, we have to construct the triangle $ABC$.
Steps of Construction :
$1.$ Draw a line segment, say $XY$ equal to $BC+CA+AB.$
$2.$ Make angles $LXY$ equal to $\angle B$ and $MYX$ equal to $\angle C.$
$3.$ Bisect $\angle LXY$ and $\angle MYX.$ Let these bisectors intersect at a point $A$.

$4$. Draw perpendicular bisectors $PQ$ of $AX$ and $RS$ of $AY$.
$5.$ Let $PQ$ intersect $XY$ at $B$ and $RS$ intersect $XY$ at $C$.
Join $AB$ and $AC$.

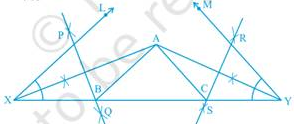
Then $ABC$ is the required triangle.

For the justification of this construction, you observe that, $B$ lies on the perpendicular bisector $PQ$ of $AX$.
Therefore, $XB=AB$ and similarly, $CY=AC$.
This gives $BC+CA+AB=BC+XB+CY=XY$
Again,
$\angle BAX=\angle AXB$ (As in $\Delta AXB,AB=XB$) and
$\angle ABC=\angle BAX+\angle AXB=2\angle AXB=\angle LXY$
Similarly,
$\angle ACB=\angle MYX$ as required.

In this chapter, you have done the following constructions using a ruler and a compass:

1. To bisect a given angle.
2. To draw the perpendicular bisector of a given line segment.
3. To construct an angle of ${60}^{\circ }$ etc.
4. To construct a triangle given its base, a base angle and the sum of the other two sides.
5. To construct a triangle given its base, a base angle and the difference of the other two sides.
6. To construct a triangle given its perimeter and its two base angles.