CIRCLES for Class 9 MATHS
INTRODUCTION
To bachcho aaj hum padhenge circles ke baare mei aur hum circles se related sari baato ko janege jaise ki circle ka circumference, radius, diameter, minor sector, major sector etc. Basically circle se related sari baato ko.
To sabse pehle aap bataye circle hota kya hai ? Aapne ye sabhi figures apne daily life mein dekhe honge. 
Ye sabhi circle ke examples hai. So, What is Circle ? To chalo hum ek fixed point consider karte hai fixed point ke around equal distance par jo points hai unke locus ko hum circle bolte hai (see all the figures carefully). English mein ese define kiya jata hai as a A circle is the locus of points equidistant from the given point. 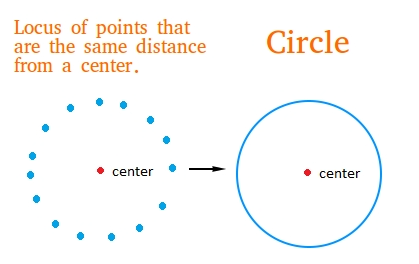
Points ki ek fixed point se jo equal distance hai ushe hum Radius ( r ) of the circle kehte hai. 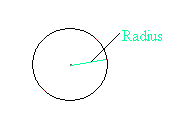
Aur es fixed point ko hum center of circle kehte hai. Ek line segment jo circle ke two different points ko join karne se bnta h, ushe Chord kehte hai.
Agar ye chord center se pass hoti hai to eshe Diameter ( d ) kehte hai. Diameter basically circle ko do equal parts mei divide karti hai.
Note→Diameter is double of radius that is d=2r. 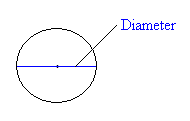
Ab humne circle ki basic information to jaan li ab hum es chapter ko thoda aur detail mein padhte hai.
Circles and its Related Terms: A Review
Toh chalo bachcho, hum kuch interesting examples se circle ke baare mein janege.
Sabse pehle aap ek compass mai ek pencil fit karle aur compass ki tip ko ek sheet par fix point par rakhe and give a name to that fixed point O. Now rotate the pencil from fix point O.
Then you will get a circle shaped figure.
Aap sabhi ko circle banana to aata hi h par kya aapko pta hai ki ek proper circle ko form karne ke liye hamesha ek fix point par hi form karna hota hai. Iss example se hume humari circle ki definition milti h.
Circle
The Collection of all points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.
Explanation
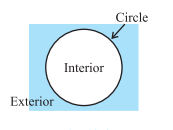
Toh abh aap ek kaam kijiye humne jo circle banaya tha usmein blue color fill kar lijiye. Toh abh jo circle ka white portion ha yani ander wala ushe hum interior kehte hai aur jo circle ke bahar ka blue portion hai ushe hum exterior kehte hai.
A circle divides the plane into three parts.
(i) interior of circle
(ii) a circle and
(iii) exterior of circle.
The circle and its interior make up the circular region.
If you take two points A and B on a circle join them passing through the center point O, then it is called the diameter of a circle.
Now if we see half distance from O to A it is called radius of the circle.
Now if you take any two points P and Q on the circumference of the circle join them without touching the center point O, so the line segment made is called chord of the circle.
P and Q points divide a circle into two parts (one longer and the another smaller). So now take a point R in between P and Q .The minor arc is PQ and the major arc is PRQ.

Now join the point from O to P and also from O to Q. It forms POQ and the formed area is called sector . So PRQO is major sector and POQ is minor sector.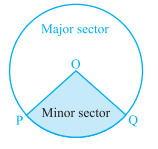
Interesting Facts
Diameter is the longest chord of a circle.
Angle Subtended by a Chord at a Point
Abh aap log ek circle par ek line segment draw kar lijiye PQ and take a point R on major arc and a point S on minor arc. Join PR and QR. Then ∠PRQ is called the angle subtended by the line segment PQ at the point R.
Join OP and OQ and it makes ∠POQ.
Join PS and QS and it makes ∠PSQ.
Theorem 10.1
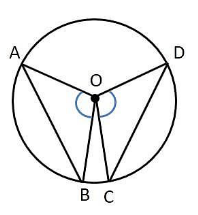
Equal chords of a circle subtend equal angles at the centre.
Given : Two equal chords AB and CD of a circle O
To prove : ∠AOB=∠COD.
Proof : In △AOB and △DOC
OA=OC ( Radii of a circle )
OB=OD ( Radii of a circle)
AB=CD (Given)
∴ △AOB≅△COD (SSS rule)
This gives, ∠AOB=∠COD
( Corresponding parts of congruent triangles).
Hence Proved.
Example 1
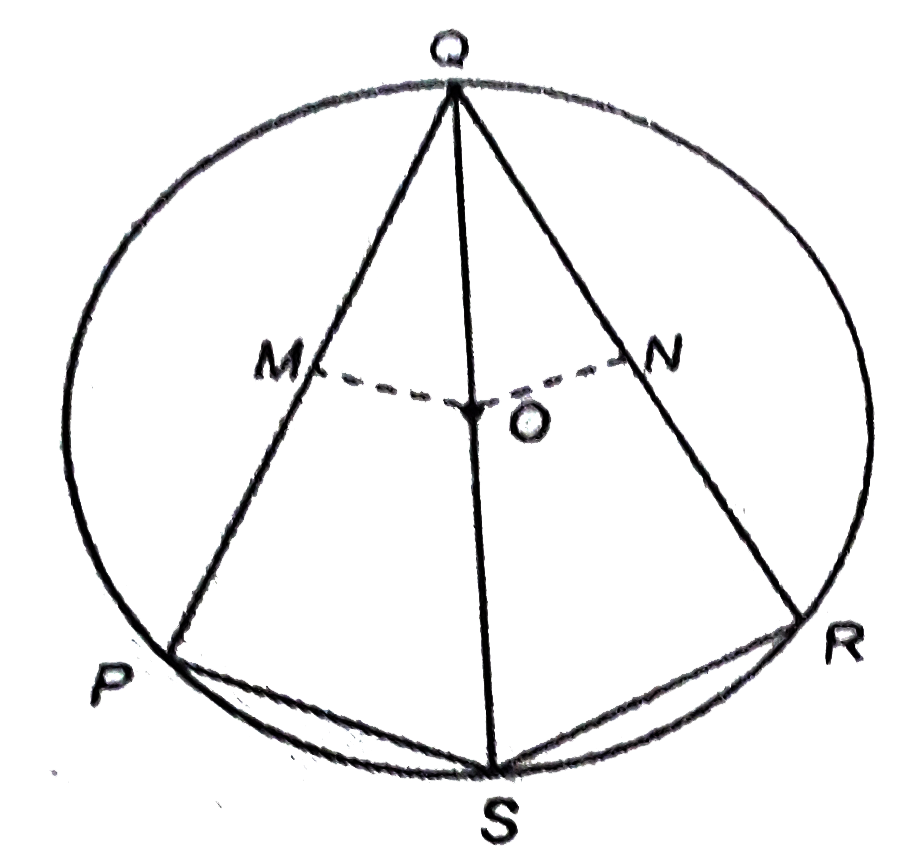
Two chords PQ and QR are equildistant form O the center of the circle. If QS, is the diameter, then show that QS bisects ∠PQR and ∠PSR.
Draw OM and ON perpendicular from O to PQ and QR respectively.
In ΔQOM and ΔQON,
∵ ⎧⎪⎨⎪⎩OM=ON(given)∠QMO=∠QNO(each90∘)QO=QO(common)
∴ΔQOM≅ΔQON (R.H.S.)
⇒∠MQO=∠NQO
Now, QS is the diameter of the circle.
∴∠QPS=∠QRS=90∘ (∵∠ in a semicircle is right angle)
In ΔQPS and ΔQRS,
∵ ⎧⎪⎨⎪⎩∠QPS=∠QRS=90∘QS=QS(common)∠PQS=∠RQS(proved above)
∴ΔQPS≅ΔQRS
⇒∠PSQ=∠RSQ
∴QS, bisects ∠PQR and ∠PSR.
Theorem 10.2
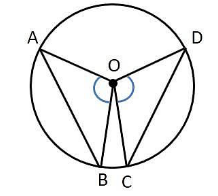
If the angles subtended by the chords of a circle at the center are equal, then the chords are equal.
Given : A circle with center at O.
AB & CD are chords that subtend equal angles at center i.e. ∠AOB=∠DOC.
To Prove : AB=CD
Proof : In △AOB & △DOC
OA=OD (Radius)
∠AOB=∠DOC (Given)
OB=OC (Radius)
Therefore, △AOB≅△COD (SAS congruency)
∴ AB=CD (CPCT)
Hence Proved.
Perpendicular from the Centre to a Chord
Sabse pehle aap log ek circle draw kare and mark the center point O. Now draw a chord AB. Abh aap log ek perpendicular line draw kare chord AB par from the center point O. Now mark a point M on chord.
Then, ∠OMA=∠OMB=90∘
OM is perpendicular to AB.
It is a property that a perpendicular bisector divide a chord or a side of a circle into two congruent parts.
So automatically MA = MB.
Example 2
Equal chords of a circle are equidistant from the centre.
Given : AB=CD
OL⊥AB and L is mid point of AB
AL=LB=12AB−(1)
OM⊥CD and M is midpoint of CD
CM=MD=12CD−(2)
AB=CD
12AB=12CD
AL=CM
In∠OMCand∠DLA
OL=OA
CM=AC
∠OMC=∠OLA
∠OMC≅∠DLA(RHS).
Example 3
Two circles of radii 5cm and 3cm intersect at two points and the distance between their centers is 4cm.
Find the length of the common chord.
By Pythagoras theorem
(5)2=(3)2+(4)2
AO=5cm
AO'=3cm
OO'=4cm
(AO)2=(AO')2+(OO')2
In ∠AOO' right angled triangle
∠AO'O=90∘
∠A'O'O is also right triangle
∠A'O'O=90∘
so,∠AO'O+∠A'O'O=180∘
AO'A' is a line with midpoint at O'<br>Common chord =2×3=6cm
Theorem 10.3
The perpendicular from the centre of a circle to a chord bisects the chord.
Given : A is a circle with center at O.
AB is a chord such that OM _|_ AB
To Prove : OM bisect chord AB i.e.
AM = BM
Proof : In△OAM&△OBM
∠OMA=∠OMB ( Both 90∘ , given)
OA=OB ( Both Radius )
OM=OM ( Common)
:. △OAM≅△OBM (RHS Rule)
AM = BM (CPCT)
Hence Proved.
Theorem 10.4
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
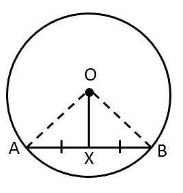
Given : A circle with center at O.
AB is chord of a circle & OX bisects AB
AX = BX
To Prove : OX _|_ AB
Proof : In △AOX & △BOX
OA =OB (Radius)
OX =OX (common)
AX =BX (Given)
∴△AOX≅△BOX (SSS)
∠AXO=∠BXO (CPCT) .....(1)
In line AB,
Hence, ∠AXO & ∠BXO form linear Pair
/_AXO + /_BXO = 180∘ (from 1)
2∠AXO=180∘
∠AXO=180∘2
∠AXO=90∘
∴∠AXO=∠BXO=90∘
=> OX _|_ AB
Hence, Proved.
Circle through Three Points
Bachcho jaisa ki aap logo ne class 6th mai padha tha ki ek line ko form karne ke liye two points sufficient hai.
So now, in class 9th a natural question arises.
How many points are sufficient to determine a circle ?
Toh sabse pehle aap ek point P draw kare aur aap dekhenge ki aap ek point se infinite circle draw kar sakte hain. Abh aap log do point Pand Q draw kare aur circle banaye aap dekhenge ki 2 point se bhi aap infinite circle draw kar sakte hain.
Abh aap log three point se circle draw karne ka try karo. Abh aap log three collinear points ( When two or more points lie on the same line, they are called collinear points.) draw kare.
If the points lie on a line, then the third point will lie inside or outside the circle passing through two points.
So now, let us take three points A, B and C, which are not collinear.
Only one circle can be obtained using three non- collinear points.
Example 4
Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then, ∠OAB=∠OAC.
Given : AB and AC are two chords of a circle.
Construction : Join OB and OC.
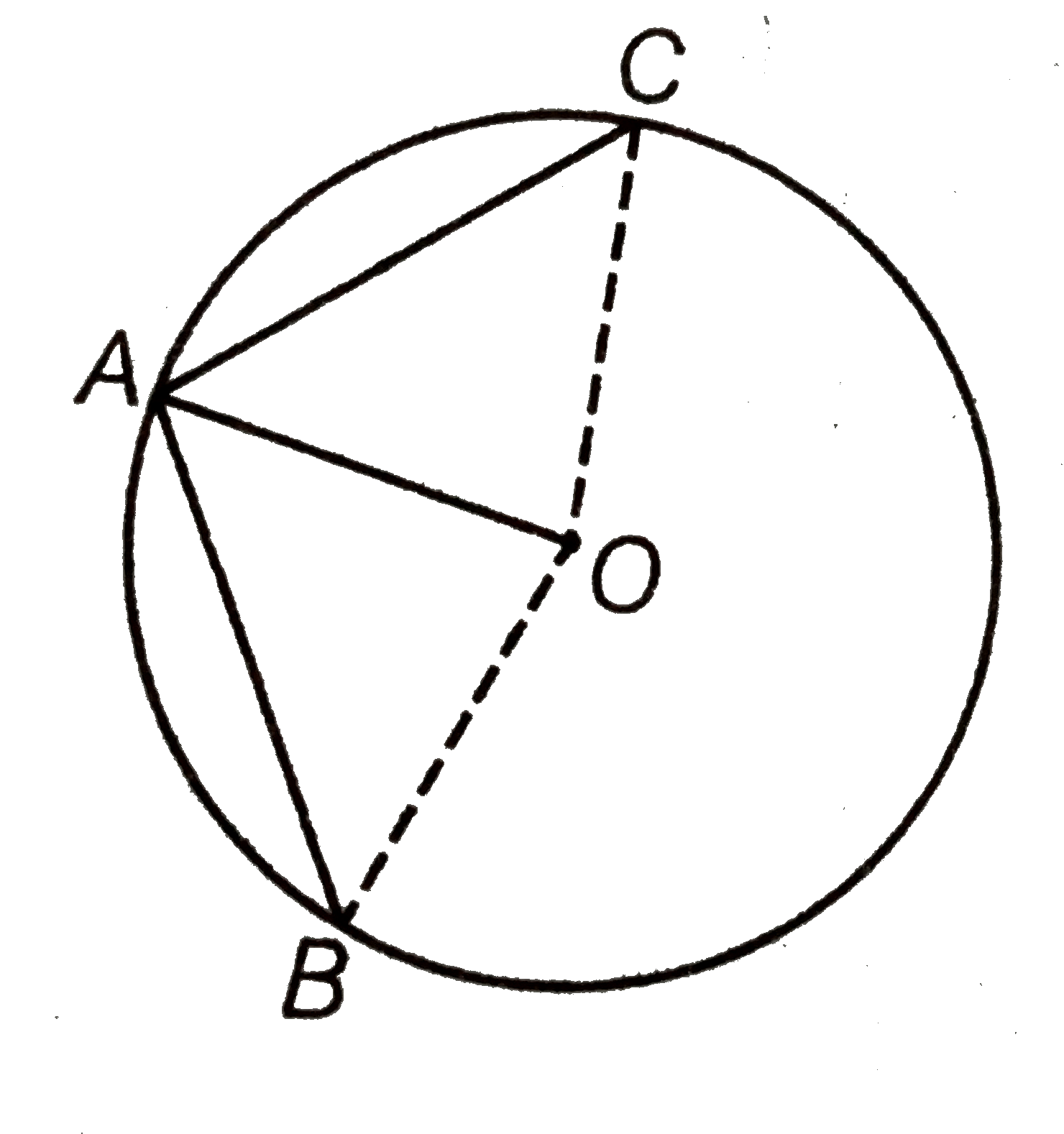
Proof : In ΔOABandΔOAC,
OA=OA [common side]
OB=OC [both are the radius of circle]
Here, we arer not able to show that either the any angle or third side is equal and ΔOAB is not congruent to ΔOAC.
∴∠OAB≠∠OAC.
Example 5
A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
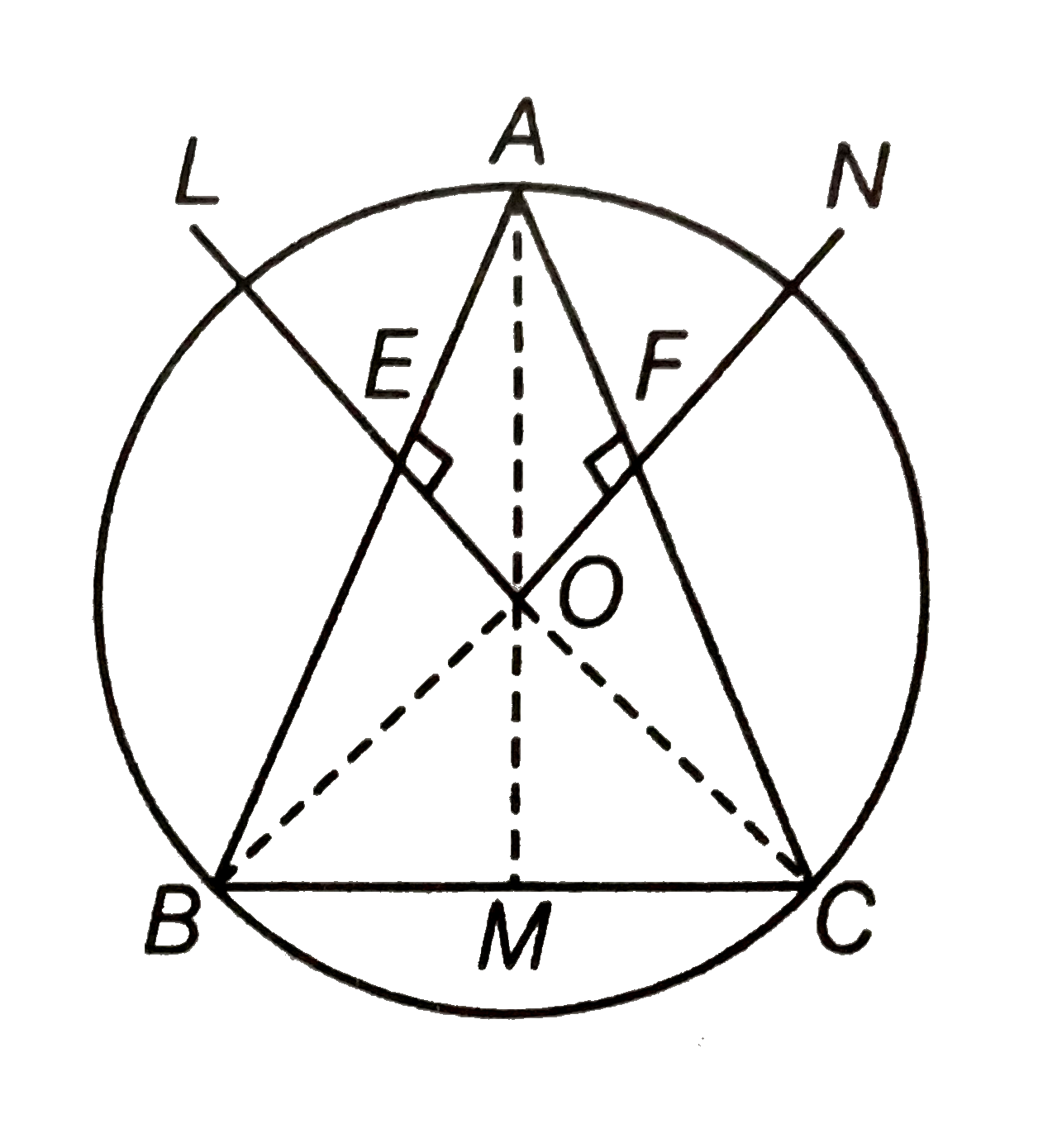
Given : A circle passing through three points, A, B and C.
Construction : Draw perpendicular bisectors of AB and AC and they meet at a point O . Join OA, OB and OC.
To prove : Perpendicular bisector of BC, also passes through O i.e, LO, ON and OM are concurrent.
Proof : In ΔOEAandΔOEB,
AE=BE
[OL is the perpendicular bisector of AB]
∠AEO=∠BEO[each 90∘]
and OE=OE [common side]
∴ΔOEA≅OEB [by SAS congruence rule]
∴OA=OB
Similarly, ΔOFA≅ΔOFC [by SAS congruence rule]
∴OA=OC [by CPCT]
∴OA=OB=OC=r [say]
Now, we draw a perpendicular from O to the BC and join them.
In ΔOMBandΔOMC,
OB=OC [proved above]
OM=OM [common side]
and ∠OMB=∠OMC[each 90∘]
∴ΔOMB≅ΔOMC [by RHS congruence rule]
⇒BM=MC [by CPCT]
Hence, OM is the perpendicular bisector of BC.
Hence, OL, ON and OM are concurrent.
Theorem 10.5
There is one and only one circle passing through three given non - collinear points.

Given : Three non - collinear points A, B, and C .
To Prove : There is one and only one circle that can be drawn through A, B and C.
Proof : Since O lies on ⊥ bisector of AB
∴OA=OB
Since O lies on ⊥ bisector of BC
∴OB=OC
=> OA=OB=OC
=> O is equidistant from A , B, and C.
=> If a circle is drawn with center O and radius OA , the circle will pass through B and C also.
Since ⊥ bisector of AB and BC cut each other at point O only.
=> O is the only point equidistant from A, B and C.
Therefore, one and only one circle can be drawn through three non - collinear points.
Equal Chords and Their Distances from the Centre
Sabse pehle hum ek chord AB draw karenge and the center point is P. So there are infinite numbers of points on a line.
L1,L2,M,L3,L4,L5.,.,.,.,
Agar aap point P ko sabhi points se join karenge toh aapko infinite line segment milenge.
Humne point P se point M par ek perpendicular draw kiya hai.
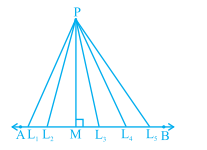
Which of the following is the shortest distance of AB from P?
Inn sabhi line segment mai se perpendicular from P to AB, namely PM.
Sabse shortest distance perpendicular se hi hota hai.
Example 6
Prove that the line joining the mid-points of two parallel chords of a circle passes through the center.
Let AB and CD be two parallel chords having P and Q as their mid-points respectively. Let O be the center of the circle. Join OP and OQ.
Now, P is the mid-points of AB.
∴OP⊥AB
⇒∠BPO=90∘
Similarly, Q is the mid-point of CD.
⇒OQ⊥CD
⇒∠DQO=90∘.
∴∠BPO+∠DQO=90∘+90∘=180∘
Also, AB || CD (given)
∴POQ must be a transversal i.e. a straight line.
⇒PQ is a straight line passing through O i.e. the center of circle.

Example 7
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, then prove that PA is angle bisector of ∠BPC.
Given : ΔABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C.
To prove : PA is an angle bisector of ∠BPC.
Construction : Join PB and PC.

Proof : Since, ΔABC is an equilateral triangle.
∠3=∠4=60∘
Now,
∠1=∠4=60∘ ...(i)
[angles in the same segment AB]
∠2=∠3=60∘ ....(ii)
[angles in the same segment AC]
∴∠1=∠2=60∘
Hence, PA is the bisector of ∠BPC.
Theorem 10.6
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
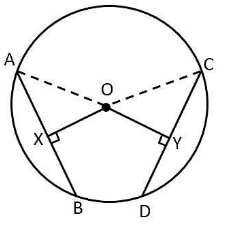
Given : A circle with center at O.
AB and CD are two equal chords of circle
i.e.AB=CD
OX and OY are perpendiculars to AB and CD respectively.
To Prove : OX =OY
Proof : Since OX _|_ AB
Perpendicular from the center to the chord, bisects the chord.
AX=BX=AB2 ...(1)
Since OY _|_ CD
Perpendicular from the center to the chord, bisects the chord.
CY=DY=CD2....(2)
Now, given that
AB=CD
AB2 = CD2
AX=CY ( From (1) and (2) )...(3)
In △AOX & △COY
∠OXA=∠OYC (Both 90∘, given)
OA=OC (Radius)
AX=CY ( from (1))
∴△AOX≅△COY ( by R.H.S Rule)
OX=OY (CPCT)
Hence, Proved.
Theorem 10.7
Chords equidistant from the centre of a circle are equal in length.
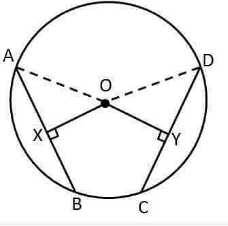
Given : A is a circle with center at O.
AB and CD are two chords of a circle where OX is distance from center i.e. OX⊥AB & OY is distance from center i.e. OY⊥CD & OX=OY
To Prove: AB = CD
Proof : In △AOX & △DOY
∠OXA=∠OYD (Both 90∘, given)
OA=OD (Radius)
OX=OY (Given)
∴△AOX≅△DOY (By R.H.S rule)
AX=DY ( CPCT)...(1)
For Chord AB
Perpendiculars from center to the chord bisects the chord.
∴ X bisects AB.
∴AB=2AX ..(2)
For Chord CD
OY⊥CD
Perpendiculars from center to the chord bisects the chord.
∴ Y bisects CD.
CD=2DY ...(3)
From (1)
AX=DY
2AY=2DY
AB=CD (From (2) & (3))
Hence, Proved.
Angle Subtended by an Arc of a Circle
Bachcho jaisa aap logo ne previous section mai dekha hai ki ek chord (except diameter) circle ko two arcs mai divide karti hai - one major and other minor.
If you take two equal chords, toh aap arcs ke size ke bareein mai kya kahenge?
Chalo iska answer aage dekhte hai.
Agar two chords ki length equal hai to wo congruent hote hai. If one arc is put on the other, without bending or twisting. Two equal chord jab center par angle banati hai to minor arc angle banati hai aur major arc reflex angle show karti hai. Congruent arcs (or equal arcs) of a circle subtend equal angles at the center.
Example 8
In the figure, AB and CD are two chords of a circle, interacting each other at a point E.
Prove that ∠AEC = 12(angle subtended by arc CXA. at the center + angle subtended by arc DYB at the center).
Given : In a figure, two chords AB and CD intersecting each other at point E.
To prove : ∠AEC=12 [angle subtended by arc CXA at center + angle subtended by arc DYB at the center]
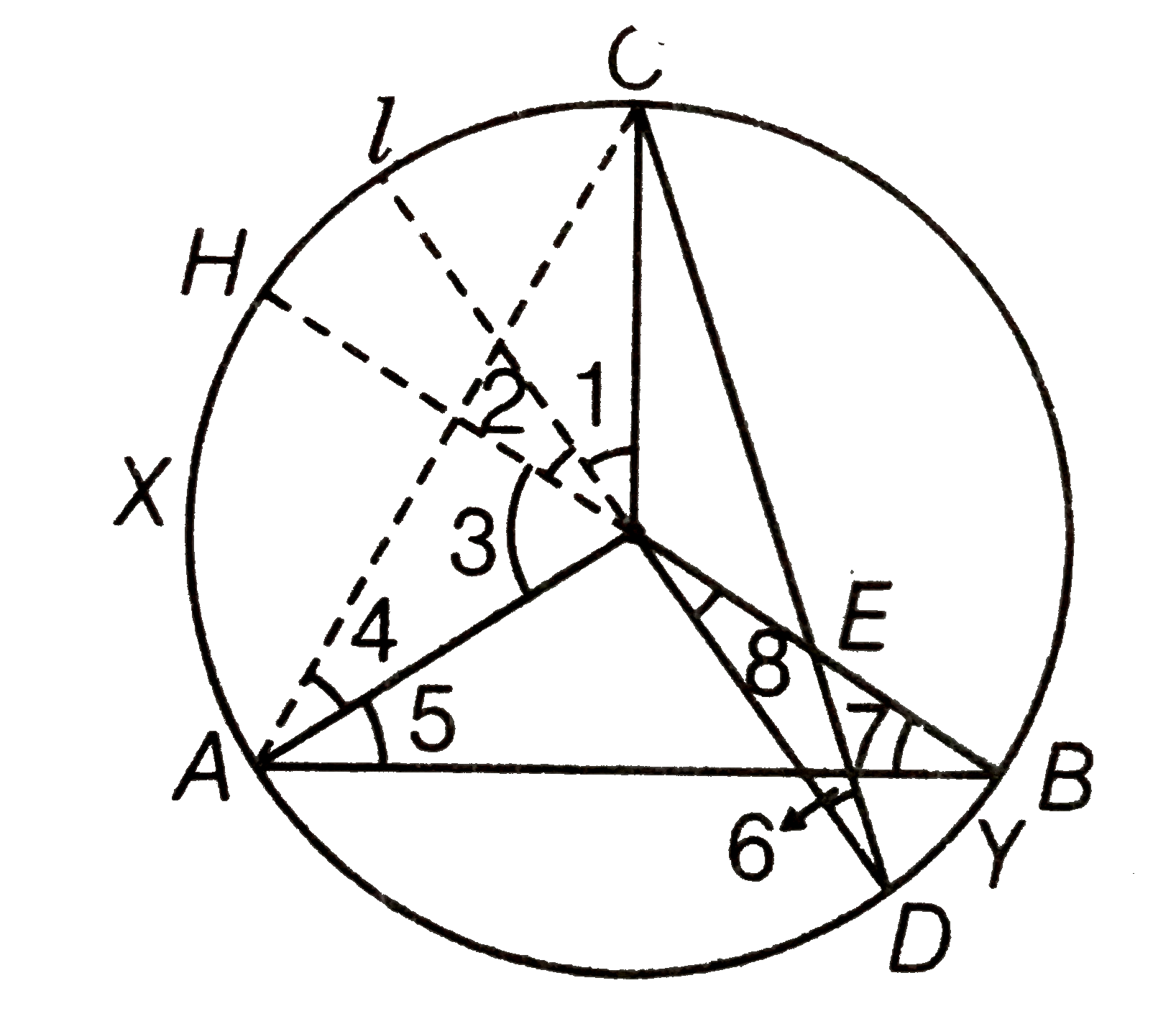
Construction : Extend the line DO and BO at the points l and H on the circle. Also, join AC.
Proof : We know that, in a circle, the angle subtended by an arc at the center is twice the angle subtended by it at the remaining part of the circle.
∴∠1=2∠6 ...(i)
and ∠3=2∠7 ....(ii)
In ΔAOC,
OC=OA [ both are the radius of circle]
∠OCA=∠4 [angles opposite to equal sides arc equal]
Also, ∠OCA+∠OCA+∠4=180∘
[by angle sum property of triangle]
⇒∠AOC+∠4+∠4=180∘
⇒∠AOC=180∘−2∠4 ...(iii)
Now, in ΔAEC,
∠AEC+∠ECA+∠CAE=180∘
[by angle property sum of a triangle]
⇒∠AEC=180∘−(∠ECA+∠CAE)
⇒∠AEC=180∘−[(∠ECO+∠OCA)+∠CAO+∠OAE]
=180∘−(∠6+∠4+∠4+∠5)
[in ΔOCD,∠6=∠ECO angles opposite to equal sides are equal]
=180∘−(2∠4+∠5+∠6)
=180∘−(180∘−∠AOC+∠7+∠6)
[from Eq. (iii) and in ΔAOB,∠5=∠7, as (angles opposite to equal sides are equal)]
∠AOC−∠32−∠12 [from Eqs. (i) and (ii)]
=∠AOC−∠12−∠22−∠32−∠22[adding and subtracting ∠22]
=∠AOC−12(∠1+∠2+∠3)+∠82[because∠2=∠8 (vertically opposite angles)]
=∠AOC−∠AOC2+∠DOB2
⇒∠AEC=12(∠AOC+∠DOB)
12 [angle subtended by arc CXA at the centre + angle subtended by arc DYB at the centre]
Example 9
In the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

Join AB.
In first circle,
AP is the diameter of the circle.
∴∠ABP=90∘ (angle in a semi-circle)
In second circle,
AQ is the diameter of the circle.
∴∠ABQ=90∘
Now, ∠ABP+∠ABQ=90∘+90∘
⇒∠PBQ=180∘
⇒PBQ is a straight line.
Theorem 10.8
The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
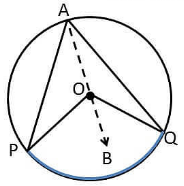
Given : A circle with center at O.
Arc PQ of this circle subtends angles POQ at center O & ∠PAQ at a point A remaining part of circle.
To Prove : ∠POQ=2∠PAQ
Construction : Join AO and extend it to point B.
Proof : There are two general cases.
Case 1 :
In △APO
OP=OA (radius)
=> ∠OPA=∠OAP (Angles opposite to equal sides are equal )...(1)
In △AQO
OQ=OA (radius)
∠OQA=∠OAQ (Angles Opposite to equal sides are equal)...(2)
Also, by exterior angle property
Exterior angle is sum of interior opposite angles.
∠BOP=∠OPA+∠OAP
∠BOP=∠OAP+∠OAP
∠BOP=2∠OAP...(3)
Also, by exterior angle property
Exterior angle is sum of interior opposite angles.
∠BOQ=∠OQA+∠OAQ
∠BOQ=∠OAQ+∠OAQ
∠BOQ=2∠OAQ...(4)
Adding (3) & (4)
∠BOP+∠BOQ = 2∠OAP+2∠OAQ
∠POQ=2(∠OAP+∠OAQ)
∠POQ=2∠PAQ
Hence Proved. 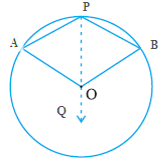
Case 2 :
In △APO
OP=OA (radius)
=> ∠OPA=∠OAP (Angles opposite to equal sides are equal)..(1)
In △AQO
OQ=OA(radius)
∠OQA=∠OAQ (Angles opposite to equal sides are equal ) ..(2)
Also, by exterior angle property
Exterior angle is sum of interior opposite angles
∠BOP=∠OPA+∠OAP
∠BOP=∠OAP+∠OAP
∠BOP=2∠OAP ...(3)
Also, by exterior angle property
Exterior angle is sum of interior opposite angles
∠BOQ=∠OQA+∠OAQ
∠BOQ=∠OAQ+∠OAQ
∠BOQ=2∠OAQ...(4)
Adding (3) and (4)
∠BOP+∠BOQ = 2∠OAP+2∠OAQ
reflex angle ∠POQ=2(∠OAP+∠OAQ)
reflex angle ∠POQ=2∠ PAQ
360∘ - ∠POQ=2∠PAQ
Hence Proved.
Theorem 10.9
Angles in the same segment of a circle are equal.
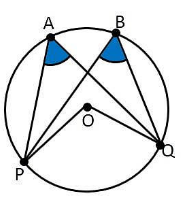
Given : A circle with center at O.
Points P & Q on this circle subtends angles ∠PAQ & ∠PBQ at points A and B respectively.
To Prove : ∠PAQ=∠PBQ
Proof : Chord PQ subtends ∠POQ at the center ( From theorem 10.8)
∴∠POQ=2∠PAQ ...(1)
∠POQ=2∠PBQ...(2)
From (1) & (2)
2∠PBQ=2∠PAQ
∠PBQ=∠PAQ
Hence, proved.
Theorem 10.10
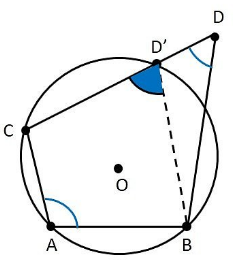
If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
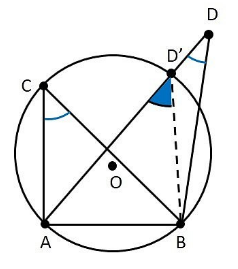
Given : A, B, C, and D are 4 points (no 3 are collinear).
AB subtends equal angles at C and D i.e. ∠ACB=∠ADB.
To Prove : A, B, C and D are concyclic.
Proof : Since A, B, C are non collinear. One circle passes through three collinear points.
Let us draw a circle C1 with center at O.
Let us assume D does not lie on C1.
Let circle intersect AD at D'
Now,
∠ACB=∠AD'B ( Angle in the same segment are equal ) ...(1)
But, given that
∠ACB=∠ADB..(2)
From (1) and (2)
∠AD'B=∠ADB...(3)
In △BDD'
∠AD'B=∠BDD'+∠D'BD (Exterior angle Property)
∠ADB=∠ADB+∠D'BD (From (3))
∠ADB−∠ADB=∠D'BD
∴∠D'BD=0
∴ D' & D are coincide.
Thus, our assumption was wrong.
=> Point D lies on circle
Therefore, A, B, C and D are concyclic.
Hence, Proved.
Cyclic Quadrilaterals
Bachcho aapne chapter 8 mai quadrilateral kai baarein mai padha tha. Toh aap log quadrilateral se familiar hain.
Toh aaj hum cyclic quadrilateral ke baarein mai padhenge. Cyclic quadrilateral wo hota hai jisme quadrilateral ke all vertices (4 vertices) ek circle pe lie kare.
Every corner of the quadrilateral must touch the circumference of the circle.
Example 10
In the figure, P is the center of the circle. Prove that : ∠XPZ=2(∠XZY+∠YXZ)

Since, arc XY subtends ∠XPY at the center and ∠XZY at a point Z in the remaining part of the circle.
∴∠XPY=2∠XZY ........(1)
Similarly, arc YZ subtends ∠YPZ at the center and ∠YXZ at a point X in the remaining part of the circle.
∴∠YPZ=2∠YXZ
Adding eqs. (1) and (2) , we have
∠XPY+∠YPZ=2∠XZY+2∠YXZ
⇒∠XPZ=2(∠XZY+∠YXZ)
Hence Proved.
Example 11
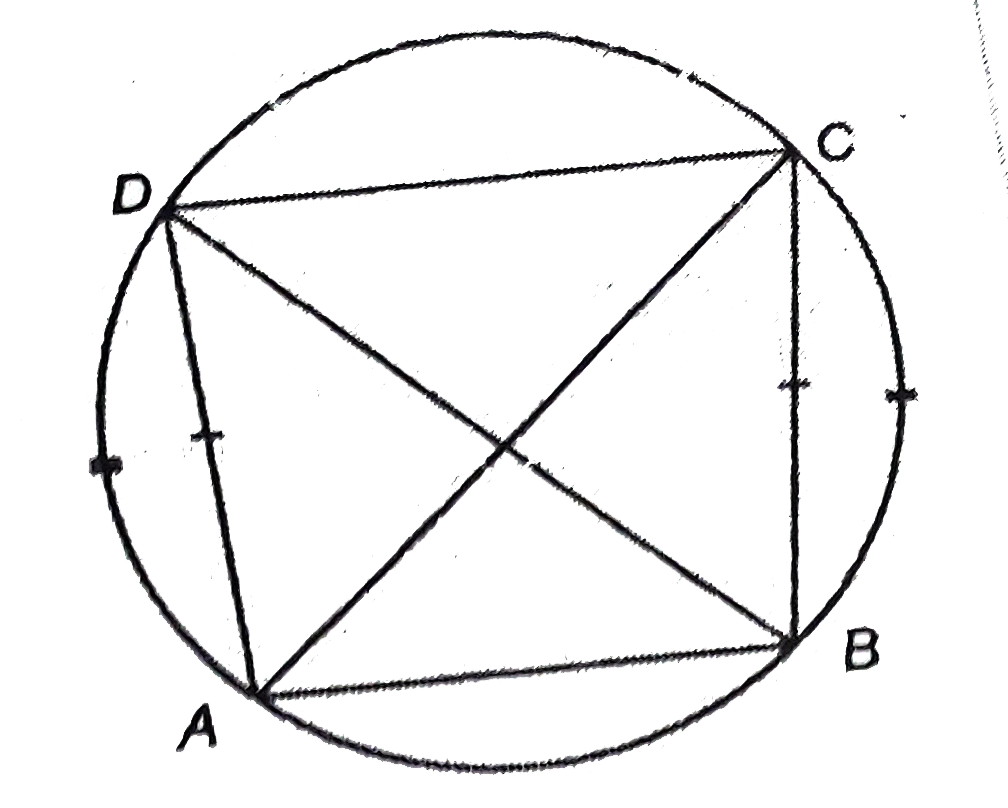
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Given : A cyclic quadrilateral ABCD in which AD=BC.
To prove: AC=BD
Proof : Because AD=BC, arc AD = arc BC
Add arc DC on both sides.
arc AD + arc DC = arc BC + arc DC
arcADC=arcBCD
AC=BD
Theorem 10.11
The sum of either pair of opposite angles of a cyclic quadrilateral is 180∘.
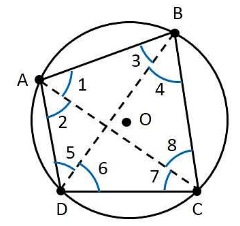
Given : ABCD is a cyclic quadrilateral of a circle with centre at O.
To prove : ∠BAD+∠BCD = 180∘
∠ABC+∠ADC = 180∘
Proof : Chord AB
∠5 = ∠8...(1) [ Angle in same segment are equal ]
Chord BC
∠1=∠6 ...(2) [ Angle in same segment are equal ]
Chord CD
∠2 = ∠4...(3) [ Angle in same segment are equal ]
Chord AD
∠7=∠3...(4) [ Angle in same segment are equal ]
By angle sum property of quadrilateral
∠A+∠B+∠C+∠D=360∘
∠1+∠2+∠3+∠4+∠7+∠8+∠5+∠6=360∘
(∠1+∠2+∠7+∠8)+(∠3+∠4+∠5+∠6)=360∘
(∠1+∠2+∠7+∠8)+(∠7+∠2+∠8+∠1)=360∘ [ From (1), (2), (3) & (4) ]
2(∠1+∠2+∠7+∠8)=360∘
∠1+∠2+∠7+∠8=180∘
(∠1+∠2)+(∠7+∠8)=180∘
∠BAD+∠BCD=180∘
Similarly,
∠ABC+∠ADC=180∘
Hence proved.
Theorem 10.12
If the sum of a pair of opposite angles of a quadrilateral is 180∘, the quadrilateral is cyclic.
Given : ABCD is a quadrilateral such that
∠BAC+∠BDC=180∘
∠ABD+∠DCA=180∘
To Prove : ABCD is a cyclic quadrilateral.
Proof : Since A, B and C are non- collinear. One circle passes through three collinear points.
Let us draw a circle C1 with center at O
Let us assume that D does not lie on C1.
Now,
∴ABCD' is a cyclic quadrilateral.
∴∠BAC+∠BD'C=180∘ (Opposite angles in a cyclic quadrilateral are supplementary)
But given
∠BAC+∠BDC=180∘
Thus,
∠BD'C=∠BDC ...(1)
Now, in△BDD'
∠BD'C=∠BDD'+∠DBD' ( Exterior angle Property )
∠BD'C=∠BDC+∠DBD'
∠BDC=∠BDC+∠DBD' (From (1))
∠BDC−∠BDC=∠DBD'
∴∠DBD'=0
∴ D' & D Coincides .
Thus, Our assumption was wrong.
=> Point D lies on circle C1
∴ ABCD' is a cyclic Quadrilateral .
Hence proved.
Summary
In this chapter, you have studied the following points:
- Ek fix point se equal distance par collection of all points, circle kehlata hai.
- Equal chords circle ke center par equal angles banati hai.
- Agar do chords circle ke center par angel form kare to wo dono chord equal hogi.
- The perpendicular from the center of a circle to a chord bisects the chord.
- Ek line circle ke center se chord ko bisect karti hai to wo chord ke perpendicular hoti hai.
- One and only one circle passing through three non - collinear points.
- Equal chords of a circle are equidistant from the centre.
- Chords equidistant from the center of a circle are equal.
- If two arcs of a circle are congruent, then their corresponding chords are equal and conversely if two chords of a circle are equal, then their corresponding arcs (minor, major) are congruent.
- Congruent arcs of a circle subtends equal angles at the center.
- The angle subtended by an arc at the center is double the angle subtended by it any point on the remaining part of the circle.
- Angles in the same segment of a circle are equal.
- Angle in a semicircle is a right angle.
- If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on the circle.
- The sum of either pair of opposite angles of a cyclic quadrilateral is 180∘.
- If sum of a pair of opposite angles of a quadrilateral is 180∘, the quadrilateral is cyclic.