हीरोन का सूत्र कक्षा 9 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम हीरोन का सूत्र (Heron's formula) का अध्ययन करेंगे। किसी भी त्रिभुज का क्षेत्रफल निकालने के लिए हीरोन ने एक सूत्र दिया, जिसे हीरोन का सूत्र (Heron's formula) कहते हैं। इस अध्याय मे हम त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा तथा चतुर्भुजों के क्षेत्रफल ज्ञात करने में हीरोन के सूत्र का अनुप्रयोग का अध्ययन करेंगे।
आइये जानते है, हीरोन के सूत्र को और करीब से...
अब तक हमने पढ़ा हैं, की त्रिभुज का क्षेत्रफल =12× आधार × ऊँचाई होता हैं तो अगर 12 से आधार और ऊँचाई का गुणा करते हैं, तो त्रिभुज का क्षेत्रफल प्राप्त हो जाता हैं। यदि हमे ऐसा त्रिभुज दिया गया हो जिसकी तीनों भुजा की लम्बाई दी गई हो, और उसकी ऊँचाई सरलता से ज्ञात न हो सकती हो, तो ऐसी स्थिति मे त्रिभुज का क्षेत्रफल ज्ञात करने के लिए हीरोन का सूत्र की आवश्यकता पड़ती हैं।
ज्यामिति में हीरोन का सूत्र (Heron's formula) त्रिभुज की तीनों भुजाएँ ज्ञात होने पर उसका क्षेत्रफल निकालने का एक सूत्र है। जिसे हीरो का सूत्र (Hero's formula) भी कहते हैं। सूत्र का यह नाम अलेक्जैण्ड्रिया हीरोन के नाम पर है।
त्रिभुज का क्षेत्रफल
हीरोन के सूत्र की आवश्यकता: यहाँ हम निम्नलिखित त्रिभुजों का क्षेत्रफल ज्ञात करेंगे जो हैं-
1. समकोण त्रिभुज
2. समबाहु त्रिभुज
3.समद्विबाहु त्रिभुज
4.विषमबाहु त्रिभुज
हम जानते हैं कि, त्रिभुज का क्षेत्रफल =12× आधार × ऊँचाई
इस सूत्र का प्रयोग कर समकोण त्रिभुज, समबाहु त्रिभुज और समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं। यदि इनकी ऊँचाई नहीं दी गई हो, तो इन त्रिभुजों की ऊँचाई ज्ञात करने के लिए हम पाइथागोरस प्रमेय का उपयोग कर सकते हैं।
आइए देखते हैं -
समकोण त्रिभुज का क्षेत्रफल

माना कि ABC एक समकोण त्रिभुज है जिसमें ∠ABC=90∘ हैं, तो AB, BC पर लंब हैं।
अतः BC= आधार तथा AB= ऊँचाई हैं।
∴△ABC का क्षेत्रफल
=12× आधार × ऊँचाई
=12(BC×AB)
समबाहु त्रिभुज का क्षेत्रफल

माना कि ABC एक समबाहु त्रिभुज है तथा AD, BC का लम्ब समद्विभाजक है।
अतः AB=BC=CA=a ( माना ) तथा AD त्रिभुज की ऊंचाई हैं।
चूंकि त्रिभुज का क्षेत्रफल
=12× आधार × ऊँचाई
अतः क्षेत्रफल निकालने के लिए इसकी ऊँचाई ज्ञात करनी होगी।
∴△ABD में पाइथागोरस प्रमेय से त्रिभुज की ऊँचाई (AD) ज्ञात कर सकते हैं
(AB)2=(AD)2+(BD)2
चूंकि AB=a और BD=a2
∴(a)2=(AD)2+(a2)2
⇒(AD)2=(a)2−(a2)2 (पक्षांतर)
⇒(AD)2=a2−a24
⇒(AD)2=a2(1−14)
⇒(AD)2=a2(4−14)
⇒(AD)2=3a24
वर्गमूल लेने पर,
AD=√3a24=√3a2
हम जानते हैं कि, त्रिभुज का क्षेत्रफल
=12× आधार × ऊँचाई
∴ त्रिभुज का क्षेत्रफल
=12×BC×AD
=12×a×√3a2
=14√3a2=√3a24
अतः समबाहु त्रिभुज का क्षेत्रफल
=√3a24
जहां a= समबाहु त्रिभुज की भुजा हैं।
समद्विबाहु त्रिभुज का क्षेत्रफल

माना कि ABC एक समद्विबाहु त्रिभुज है तथा AD, BC का लम्ब समद्विभाजक है।
जिसमे AB=AC=a और BC=b तथा AD त्रिभुज की ऊंचाई हैं।
तथा BD=DC=b2
हम जानते हैं कि, त्रिभुज का क्षेत्रफल
=12× आधार × ऊँचाई
△ABD में पाइथागोरस प्रमेय से त्रिभुज की ऊँचाई (AD) ज्ञात कर सकते हैं।
(AB)2=(AD)2+(BD)2
⇒(a)2=(AD)2+(b2)2
⇒(AD)2=(a)2−(b2)2
⇒(AD)2=a2−b24
⇒(AD)2=4a2−b24
⇒AD=√4a2−b22
∴ त्रिभुज का क्षेत्रफल
=12×BC×AD
=12×b×√4a2−b22
=14b(√4a2−b2)
अतः समद्विबाहु त्रिभुज का क्षेत्रफल
=14b(√4a2−b2)
जहां बराबर भुजाओं में से प्रत्येक a है तथा आधार (तीसरी भुजा) b है।
अतः स्पष्ट हैं कि किसी समकोण त्रिभुज, समबाहु त्रिभुज और समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग कर सकते हैं-
त्रिभुज का क्षेत्रफल
=12× आधार × ऊँचाई
लेकिन इस सूत्र का प्रयोग विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए नहीं कर सकते हैं, चूंकि क्षेत्रफल ज्ञात करने के लिए ऊँचाई ज्ञात करनी होगी और अगर विषमबाहु त्रिभुज के प्रश्न में ऊँचाई नहीं दी गई हैं तो इसकी ऊँचाई ज्ञात नहीं कर सकते हैं इसलिए विषमबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए इस सूत्र का प्रयोग नहीं कर सकते हैं।
अतः इसका क्षेत्रफल हीरोन का सूत्र (Heron's formula) से ज्ञात कर सकते हैं जिसे हम आगे पढ़ने वाले हैं।
त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा
माना की ΔABC एक त्रिभुज हैं जिसकी भुजाएँ क्रमशः a, b और c हैं।
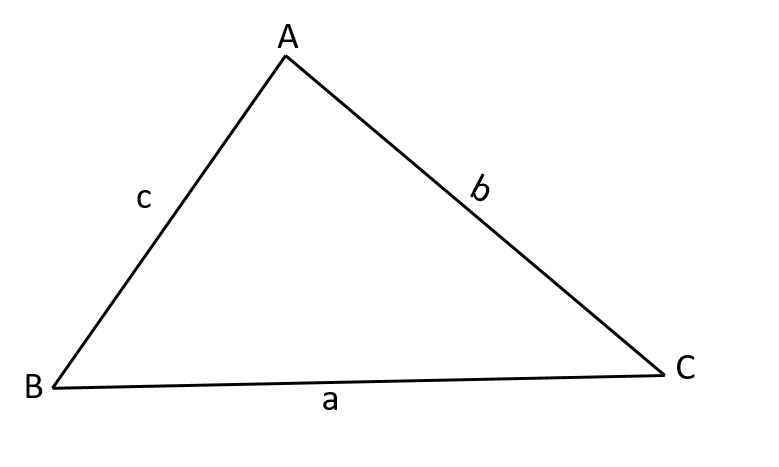
अतः
हीरोन का सूत्र से,
त्रिभुज का क्षेत्रफल =√s(s−a)(s−b)(s−c)
जहाँ s = त्रिभुज का अर्धपरिमाप (semi-perimeter) =a+b+c2
यह सूत्र उस स्थिति में उपयोगी है जब त्रिभुज की ऊँचाई सरलता से ज्ञात नहीं की जा सकती हो।
जैसे - यदि एक त्रिभुज की भुजाएँ 15 m, 11 m और 6 m हैं, त्रिभुज क्षेत्रफल ज्ञात करें।
हल: माना कि △ABC की भुजाएँ a=15 m, b=11 m और c=6 m हैं।
अतः हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल =√s(s−a)(s−b)(s−c)
यहाँ s= त्रिभुज का अर्धपरिमाप
अत:, त्रिभुज का अर्धपरिमाप,
s=a+b+c2=15+11+62=322=16m
=√16(16−15)(16−11)(16−6)
=√16(1)(5)(10)
=√4×4×(1)(5)(5×2)
=4×5√2
=20√2m2
अत: त्रिभुज का क्षेत्रफल 20√2m2 हैं।
उदाहरण 1
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसकी भुजाओं की लम्बाई 13 सेमी, 14 सेमी तथा 15 सेमी है।
दिया हैं,
त्रिभुज की भुजायें 13 सेमी, 14 सेमी और 15 सेमी हैं ।
त्रिभुज का क्षेत्रफल = ?
हम जानते हैं, की हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल =√s(s−a)(s−b)(s−c)
अतः
a=13 सेमी, b=14 सेमी और c=15 सेमी
तथा अर्धपरिमाप s=a+b+c2=13+14+152=21
∴ त्रिभुज का क्षेत्रफल =√21×(21−13)×(21−14)×(21−15)
=√21×8×7×6
=√7×3×8×7×2×3
=√72×42×32
=7×4×3=84 सेमी 2
अतः त्रिभुज का क्षेत्रफल 84 सेमी 2 हैं।
उदाहरण 2
एक समद्विबाहु त्रिभुज का परिमाप 30 सेमी तथा इसकी समान भुजाओं की लम्बाई 12 सेमी है। त्रिभुज का क्षेत्रफल ज्ञात कीजिये।
दिया हैं,
चूंकि समद्विबाहु त्रिभुज की दो भुजा समान होती हैं।

यहाँ दो भुजा AB और AC, 12सेमी हैं।
तथा माना की तीसरी भुजा BC, x सेमी हैं।
परिमाप = 30 सेमी
हम जानते हैं की, परिमाप त्रिभुज की तीनों भुजा की लंबाई का योगफल होता हैं।
∴ परिमाप =AB+BC+CA
⇒30=12+x+12
⇒30=24+x
⇒x=6 सेमी
चूंकि परिमाप 2s=30 सेमी
∴ अर्धपरिमाप s=15 सेमी
अतः क्षेत्रफल =√s(s−a)(s−b)(s−c)
( यहाँ a=b=12 सेमी तथा c=6 सेमी हैं )
=√15×(15−12)×(15−12)×(15−6)
=√15×3×3×9
=√15×9×9
=9√15 सेमी 2
अतः त्रिभुज का क्षेत्रफल 9√15 सेमी 2 हैं।
उदाहरण 3
एक त्रिभुज की भुजाओं का अनुपात 12:17:25 हैं और उसका परिमाप 540 सेमी है त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
माना कि त्रिभुज की भुजाएँ 12x, 17x तथा 25x हैं।
चूंकि परिमाप 540cm हैं
अतः 12x+17x+25x=540
⇒54x=540
⇒x=10
त्रिभुज की भुजाएँ
a=12×10=120cm
b=17×10=170cm
c=25×10=250cm
∴ अर्धपरिमाप s=a+b+c2
=120+170+2502
=5402=270cm
अतः हीरोन के सूत्र से, त्रिभुज का क्षेत्रफल
=√s(s−a)(s−b)(s−c)
=√270×(270−120)
×(270−170)×(270−250)
=√81000000
=9000cm2
अतः दिए गए त्रिभुज का क्षेत्रफल 9000 cm2 हैं।
उदाहरण 4
किसी पार्क में एक फिसल पट्टी (slide) बनी हुई है। इसकी पार्श्वीय दीवारों (side walls) में से एक दीवार पर किसी रंग से पेंट किया गया है उस पर "पार्क को हरा - भरा और साफ़ रखिये '' लिखा हुआ है। यदि इस दीवार की विमाएँ 15 m, 11m और 6 m है, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिये।

दिया हैं,
त्रिभुज की भुजाएँ a=15m,b=11m और c=6m हैं।
अतः हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल
=√s(s−a)(s−b)(s−c)
यहाँ s= त्रिभुज का अर्धपरिमाप
अत:, त्रिभुज का अर्धपरिमाप,
s=a+b+c2
=15+11+62
=322=16m
=√16×(16−15)×(16−11)
×(16−6)
=√16(1)(5)(10)
=√4×4×(1)(5)(5×2)
=4×5√2
=20√2m2
अतः, रंग से पेंट हुए भाग का क्षेत्रफल 20√2m2 है।
चतुर्भुजों का क्षेत्रफल ज्ञात करने में हीरोन के सूत्र का अनुप्रयोग
एक चतुर्भुज जिसकी भुजाएँ तथा एक विकर्ण दिए हों, तो उसका क्षेत्रफल ज्ञात करने के लिए उसे दो त्रिभुजों में विभाजित करके और फिर हीरोन के सूत्र का प्रयोग करके, विभाजित किए गए त्रिभुजों को जोड़ने पर, चतुर्भुज का क्षेत्रफल ज्ञात किया जा सकता है।
आकृति मे देख सकते हैं की चतुर्भुज ABCD में विकर्ण खींचकर दो भागों मे विभाजित किया गया हैं, ΔABC और ΔADC
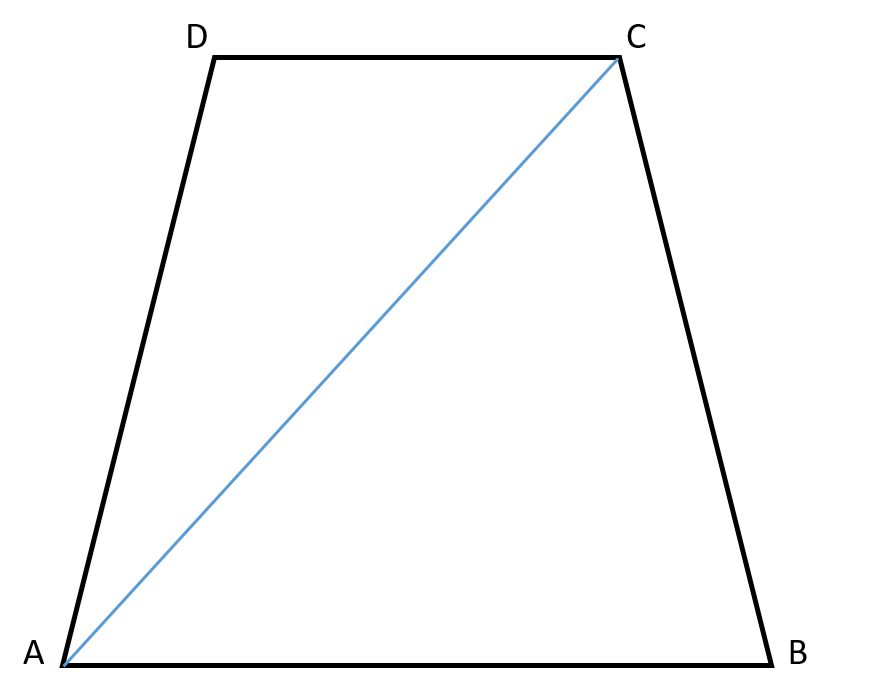
अतः चतुर्भुज ABCD का क्षेत्रफल = त्रिभुज ABC का क्षेत्रफल + त्रिभुज ADC का क्षेत्रफल
चतुर्भुज का क्षेत्रफल ज्ञात करने की आवश्यकता हमें दैनिक जीवन में भी पड़ती है। उदाहरण के लिए किसी किसान के पास एक जमीन का प्लॉट चतुर्भुज आकार का है और वह इसका क्षेत्रफल मालूम करना चाहता है। चतुर्भुज का क्षेत्रफल निकालने के लिए चतुर्भुज को किसी विकर्ण द्वारा दो त्रिभुजों में बाँटकर और तब अलग-अलग हीरोन के सूत्र का प्रयोग से दोनों त्रिभुजों का क्षेत्रफल ज्ञात कर और उन्हें जोड़कर पूरे चतुर्भुज का क्षेत्रफल निकाल सकते है।
उदाहरण 5
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिये जिसकी भुजाएँ क्रमशः 9 मी, 40 मी, 28 मी तथा 15 मी लम्बाई की है और पहली दो भुजाएँ के बीच का कोण समकोण है।
मान लीजिये दिया गया चतुर्भुज ABCD इस प्रकार है
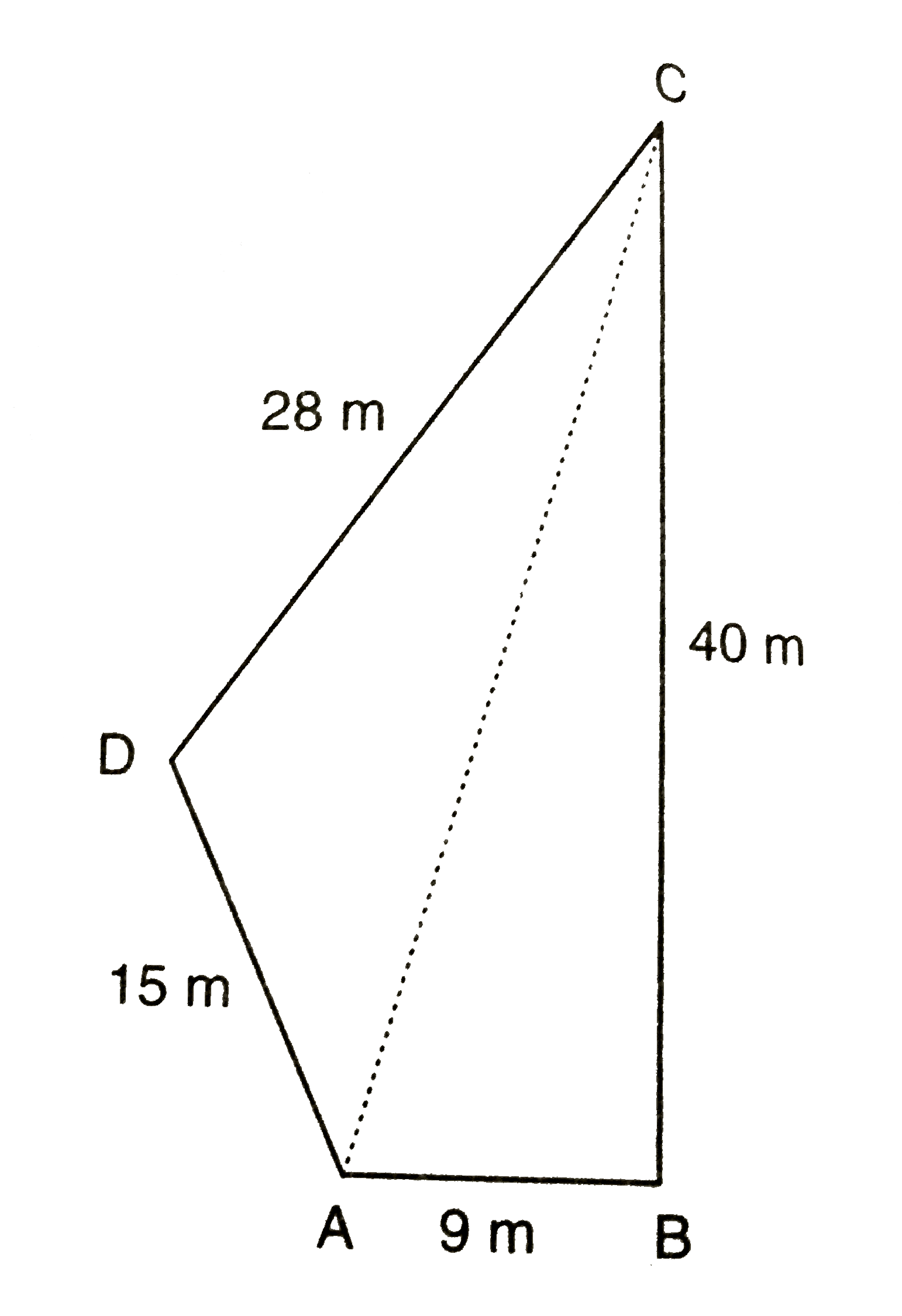
दिया हैं,
पहली दो भुजाओं के बीच का कोण समकोण है।
अतः ∠ABC=90∘
तथा AB=9 मी, BC=40 मी, CD=28 मी, AD=15 मी
चतुर्भुज ABCD का क्षेत्रफल =?
चूंकि चतुर्भुज ABCD को 2 त्रिभुजों ΔACD और ΔABC में विभाजित किया जा सकता है।
अतः चतुर्भुज ABCD का क्षेत्रफल =(ΔABC का क्षेत्रफल ) + (ΔACD का क्षेत्रफल )
ΔABC से, हम AC ज्ञात कर सकते हैं।
AC2=AB2+BC2 [पाइथागोरस प्रमेय द्वारा ]
⇒AC2=92+402=1681
⇒AC=41 मी
∴ΔABC का क्षेत्रफल =12 (आधार × ऊँचाई )
⇒ΔABC का क्षेत्रफल =12(AB×BC)
⇒ΔABC का क्षेत्रफल =12(9×40) मी 2 = 180 मी 2
अब ΔACD में,
AC=41 मी, CD=28 मी तथा DA=15 मी
माना की a=AC=41 मी, b=CD=28 मी तथा c=DA=15 मी
चूंकि अर्धपरिमाप s=a+b+c2=41+28+152=842=42 मी
∴ΔACD का क्षेत्रफल =√s(s−a)(s−b)(s−c)
⇒ΔACD का क्षेत्रफल
=√42(42−41)(42−28)(42−15)
=√42×1×14×27=√14×3×14×27
=√14×14×3×3×9
=√14×14×9×9
=14×9=126 मीटर 2
अतः चतुर्भुज ABCD का क्षेत्रफल =(ΔABC का क्षेत्रफल ) + (ΔACD का क्षेत्रफल )
=(180+126) मी 2
=306 मी 2
अतः चतुर्भुज ABCD का क्षेत्रफल 306 मी 2 हैं।
उदाहरण 6
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिये जिसमे AB=7 सेमी, BC=6 सेमी, CD=12 सेमी, DA=15 सेमी तथा AC=9 सेमी है।
दिया हैं,
AB=7 सेमी, BC=6 सेमी, CD=12 सेमी, DA=15 सेमी तथा AC=9 सेमी
विकर्ण AC चतुर्भुज ABCD को दो त्रिभुजों ΔABC तथा ΔACD में विभाजित करता है।
चतुर्भुज ABCD का क्षेत्रफल =?
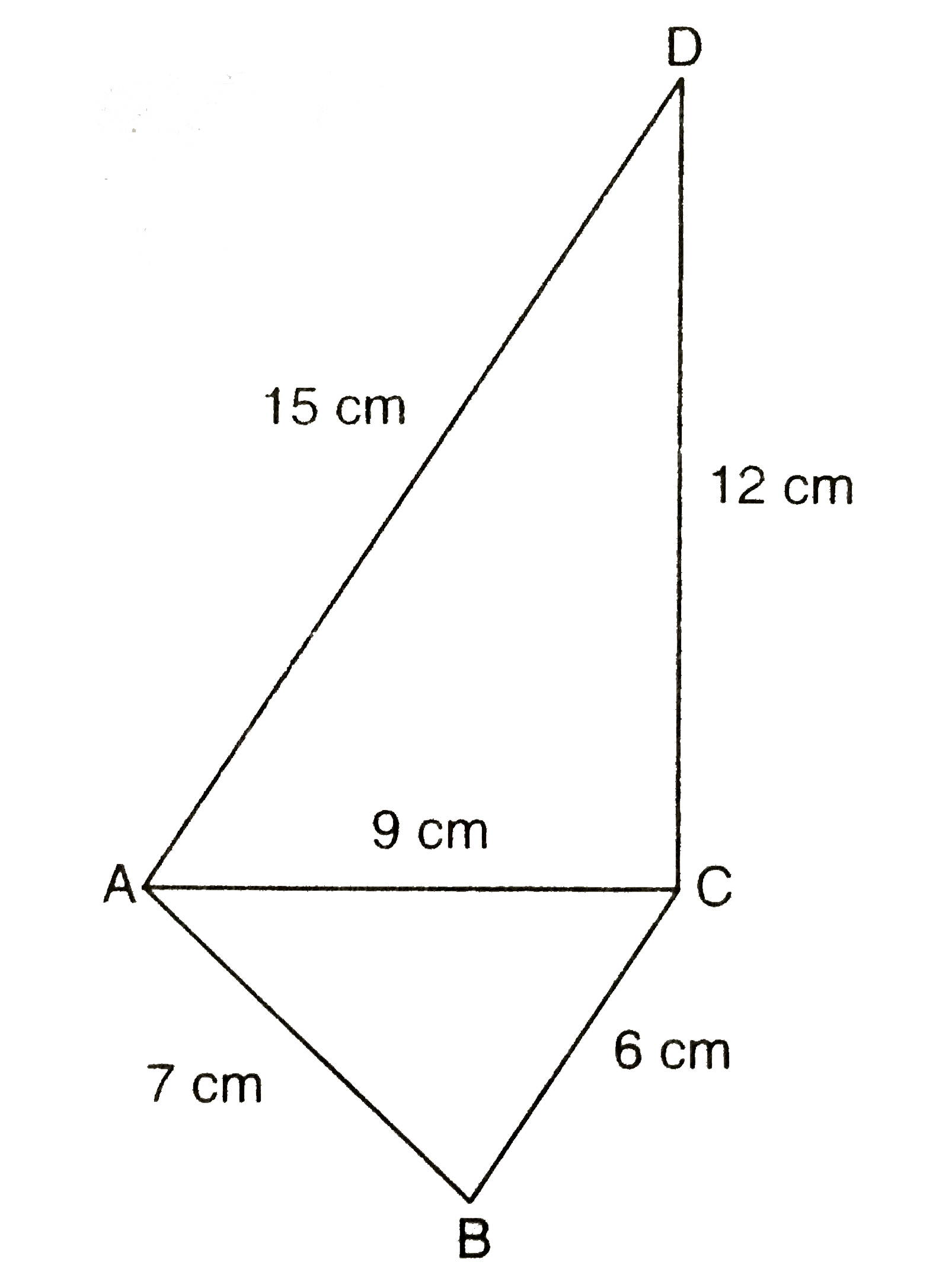
∴ चतुर्भुज ABCD का क्षेत्रफल =ΔABC का क्षेत्रफल +ΔACD का क्षेत्रफल
त्रिभुज ABC के लिए,
अर्द्धपरिमाप s=6+7+92
=11 सेमी
∴ΔABC का क्षेत्रफल
=√s(s−a)(s−b)(s−c)
=√11(11−6)(11−7)(11−9)
=√11×5×4×2
=√440 सेमी 2
=20.98 सेमी 2
त्रिभुज ACD के लिए,
अर्द्धपरिमाप s=9+12+152
=18 सेमी
∴ΔACD का क्षेत्रफल
=√18(18−9)(18−12)(18−15)
=√18×9×6×3=√18×9×6×3
=√2916= 54 सेमी 2
∴ चतुर्भुज ABCD का क्षेत्रफल =(20.98+54) सेमी 2=74.98 सेमी 2
अतः चतुर्भुज ABCD का क्षेत्रफल 74.98 सेमी 2 हैं।
उदाहरण 7
राधा ने एक रंगीन कागज से एक हवाईजहाज का चित्र बनाया, जैसा की आकृति में दिखाया गया है। प्रयोग किये गए कागज का कुल क्षेत्रफल ज्ञात कीजिये।
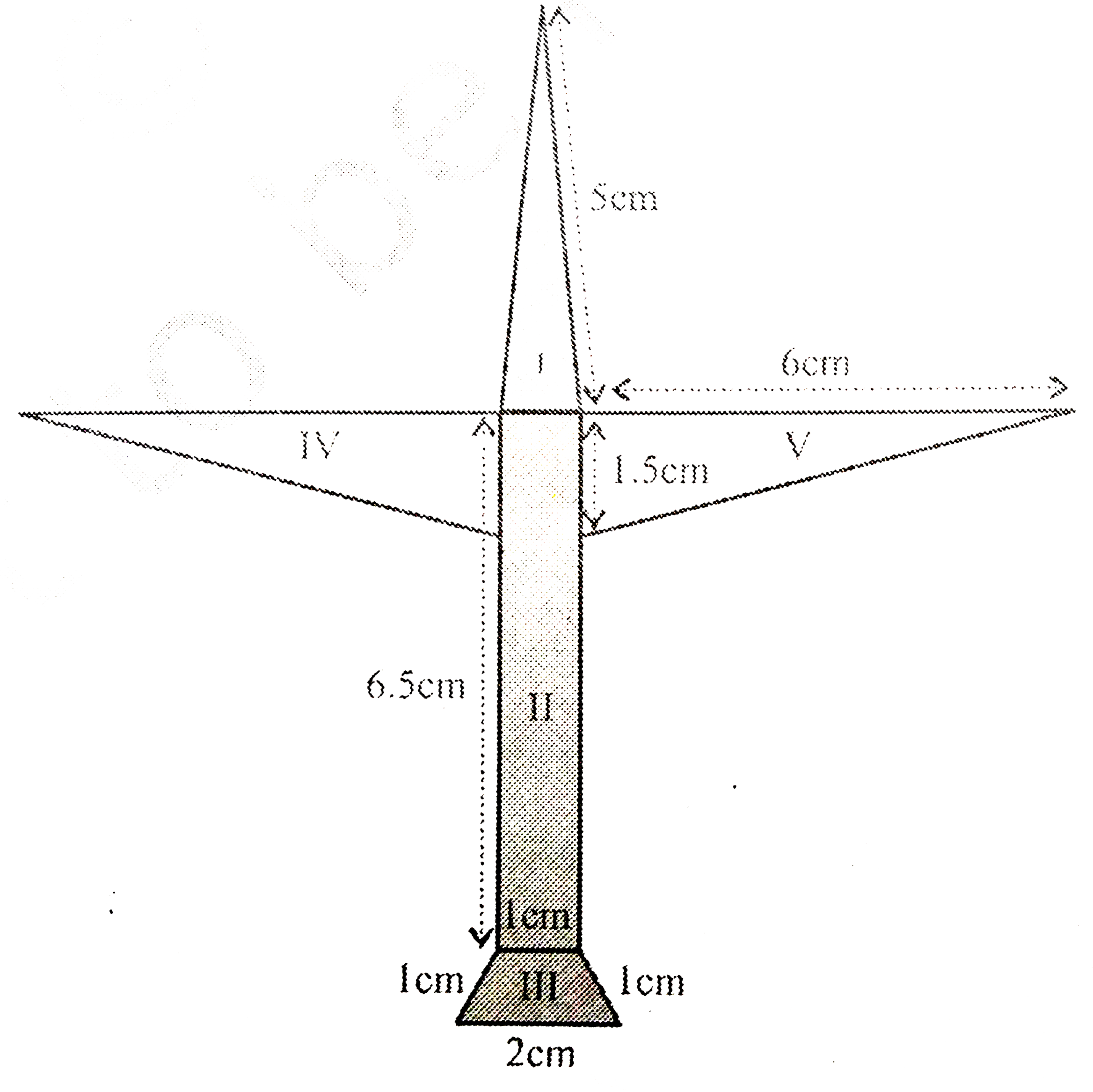
यहाँ कागज को 5 भागों मे विभाजित किया गया हैं।
प्रयोग किए गए कागज का कुल क्षेत्रफल = भाग I का क्षेत्रफल + भाग II का क्षेत्रफल + भाग III का क्षेत्रफल + भाग IV का क्षेत्रफल + भाग V का क्षेत्रफल
भाग I के लिए,
यहाँ, त्रिभुज की भुजाएँ a=5 cm, b=5 cm और c=1 cm हैं।
अत:, त्रिभुज का अर्धपरिमाप,
s=a+b+c2=5+5+12=112=5.5 cm
इसलिए, हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल
=√s(s−a)(s–b)(s−c)
=√5.5(5.5−5)(5.5−5)(5.5−1)
=√5.5(0.5)(0.5)(4.5)
=√6.1875
=2.49cm2
भाग II के लिए,
यहाँ, आयत की भुजाएँ l=6.5cm और b=1 cm हैं|
इसलिए, आयत का क्षेत्रफल =l×b=6.5×1=6.5cm2
भाग III के लिए,
यह एक समलंब चतुर्भुज हैं।
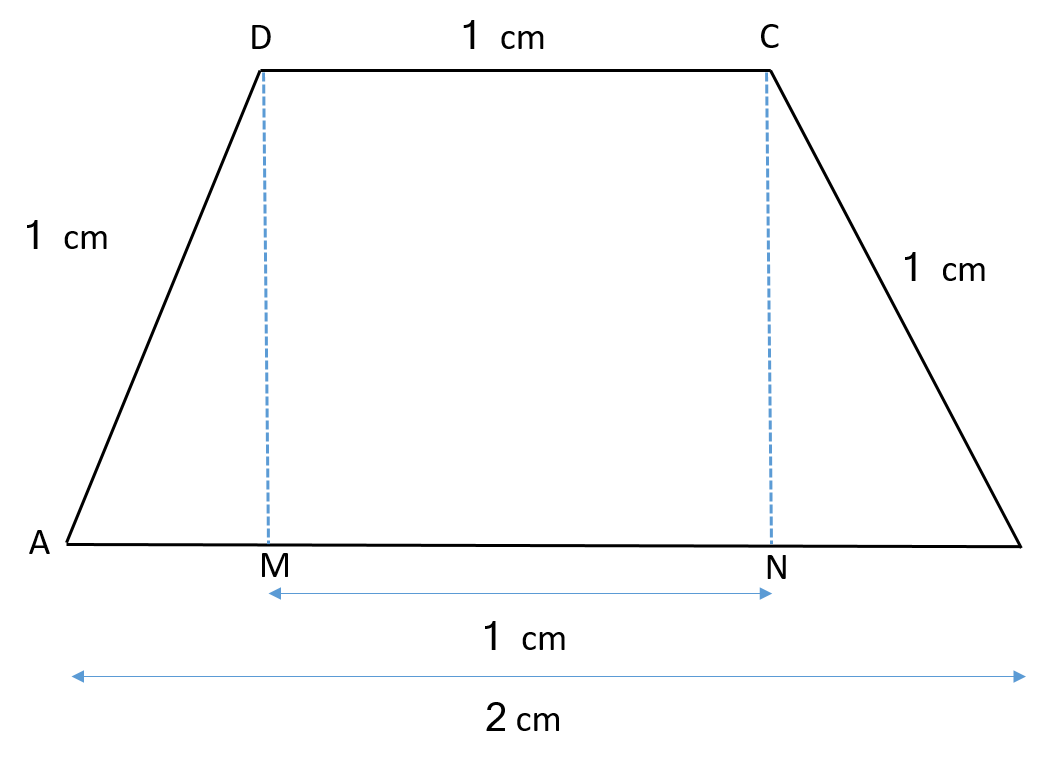
समलंब की ऊंचाई NC=DM=h=√(1)2−(12)2
=√1−14 =√34 =√32 cm
चूंकि समलंब का क्षेत्रफल =12×(a+b)×h
यहाँ भुजा a=1 cm, b= 2 cm तथा ऊँचाई h=√32 cm
समलंब का क्षेत्रफल =12×(1+2)×√32
=12×3×√32
=34×√3
=0.75×√3
=0.75×1.732
=1.29cm2
भाग IV के लिए,
यहाँ, त्रिभुज का आधार 1.5 cm और ऊँचाई 6 cm है।
इसलिए, त्रिभुज का क्षेत्रफल =12× आधार × ऊँचाई
=12×1.5×6
=4.5 cm2
भाग V के लिए,
चूंकि भाग IV और भाग V का दोनों ही त्रिभुज की भुजाओं की लंबाई समान हैं अतः क्षेत्रफल भी समान होगा।
अतः प्रयोग किए गए कागज का कुल क्षेत्रफल = भाग । का क्षेत्रफल + भाग II का क्षेत्रफल + भाग III का क्षेत्रफल + भाग IV का क्षेत्रफल + भाग V का क्षेत्रफल
=2.49+6.5+1.29+4.5+4.5
=19.28cm2
अतः प्रयोग किए गए कागज का कुल क्षेत्रफल 19.28cm2 हैं।
उदाहरण 8
एक पतंग भिन्न -भिन्न शेडों (shades) के कागजों से बनी है। इन्हे आकृति में I,II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6cm, 6 cm और 8 cm भुजाओं का भाग समद्विबाहु त्रिभुज है। ज्ञात कीजिये की प्रत्येक शेड का कितना कागज प्रयुक्त किया है।
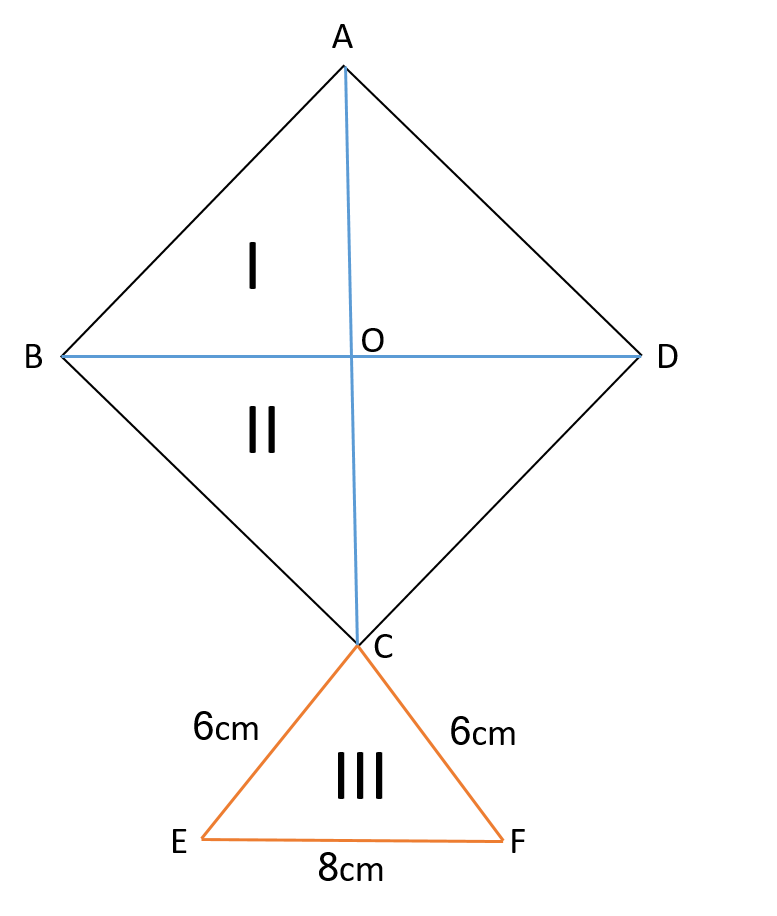
दिया हैं,
विकर्ण AC=BD=32cm
तथा AO=OC=OD=OB=16cm
[वर्ग के विकर्ण एक दूसरे के बराबर होते हैं तथा समद्विभाजित करते हैं।]
प्रत्येक शेड का क्षेत्रफल =?
भाग I में प्रयुक्त कागज =ΔABC का क्षेत्रफल
∴ΔABC का क्षेत्रफल =12× आधार × ऊँचाई
=12×BD×AO
=12×32×16
=12×2×16×16
= 1/cancel(2) xx cancel(2)xx 16 xx 16
=256 cm2
अतः, शेड I में प्रयुक्त कागज 256cm2 है।
इसी प्रकार,
भाग II में प्रयुक्त कागज =ΔCDB का क्षेत्रफल
∴ΔCDB का क्षेत्रफल =12× आधार × ऊँचाई
=12×BD×OC
=12×32×16
=12×2×16×16
= 1/cancel(2) xx cancel(2)xx 16 xx 16
=256 cm2
अतः, शेड II में प्रयुक्त कागज 256cm2 है।
इसी प्रकार,
भाग III में प्रयुक्त कागज =ΔCEF का क्षेत्रफल
हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल =√s(s−a)(s−b)(s−c)
यहाँ a=6 cm, b=6 cm, तथा c=8 cm
अर्धपरिमाप s=a+b+c2=6+6+82=202=10 cm
ΔCEF का क्षेत्रफल =√10(10−6)(10−6)(10−8)
=√10(4)(4)(2)
=√2×5×2×2×2×2×2
=(2×2×2)√5
=8√5
अतः, शेड III में प्रयुक्त कागज 8√5 cm2 है।
सारांश
जहाँ s=a+b+c2 है।