RATIONAL NUMBERS for Class 8 MATHS
Types of Numbers
1. Natural Numbers (N)
Basically jitne bhi counting numbers hote hai wo sab natural number kahlate hai i.e., N=1,2,3...
2. Whole Numbers (W)
Agar hum natural number mein 0 add karde to wo whole numbers khlate hai.
W=0,1,2,3,...
→ Ab humne natural numbers aur whole numbers dono ki baat kr li lekin agar mai aapse puchu ki 0 se pehle kya aata hai to aapka answer hoga −1, aur usse pehle −2,−3.... and so on. Ye sabhi negative numbers khlate hai.
3. Integers (Z)
Bachcho negative numbers aur whole numbers dono ko ek saath hum integers kahte hai. Lekin apko yah dhyan rakhna hai ki aise numbers jo fractional ya decimal form mein hote hai unhe hum integers nhi kahte.
Note : → Negative Integers are {−1,−2,−3,−4,−5,...}
Non negative numbers or whole numbers are {0,1,2,3,4,5,...}
We can put that all together like this:
(Z)={...,−4,−3,−2,−1,0,1,2,3,4,...}
4. Rational Numbers (Q)
Bachcho rational numbers wo numbers hote hai jo ki pq (where p and q are integers), ki form mei represent kiye jate hai, where q≠0.
Properties of Rational Numbers
Closure Property : A set of a number is said to be closed for a specific mathematical operation if the result obtained when that operation is performed on any numbers in the set, is itself a member of that set. If a set of number is said to be closed for a particular operation then it is said to possess the closure property for that operation.
Bachcho in short iska mtlb ye hai ki agar hum kisi number ke collection (N,W,Z,Q) mein koi mathematical operation yani addition, subtraction, multiplication ya division apply karte hai to jo result ayega wo usi set se belong karta hai to wo set closure property show karega otherwise nhi for that mathematical operation.
Whole Number
| Operations | Numbers | Remarks |
|---|---|---|
| Addition | 8+0=8, a whole number 9+7=16, which is a whole number. In general, a+b is whole number for any two whole numbers a and b (Bachcho agar hum kisi bhi 2 whole numbers ko add karte hai to result bhi ek whole number ata hai). |
Whole numbers are closed under addition. |
| Subtraction | 8−9=−1, which is not a whole number while if we subtract 9 from 10 then we get 1 as the result, which is a whole number. (Bachcho hum dekh sakte hai ki agar hum 2 whole numbers ka subtraction kare to ye jaruri nhi hai ki result bhi ek whole number aye) |
Whole numbers are not closed under subtraction. |
| Multiplication | 0×5=0, a whole number 4×6=24, which is a whole number. In general, if a and b are two whole numbers, their product ab is a whole number (Bachcho hum dekh sakte hai ki agar hum 2 whole numbers ka multiplication kare to result ek whole number hi ayega). |
Whole numbers are closed under multiplication. |
| Division | 4÷5=45 which is not a whole number while if we divide 9 by 3 then the result we get 3, which is a whole number. (Bachcho hum dekh sakte ye jaruri nhi hai ki jab hum 2 whole numbers ko divide kare to result bhi ek whole number aye) |
Whole numbers are not closed under division. |
Integers
| Operations | Numbers | Remarks |
|---|---|---|
| Addition | −8+6=−2, is an integer 9+7=16, which is an integer. In general, a+b is an integer for any two integers a and b.(Bachcho hum dekh sakte hai ki jab hum kisi bhi 2 integers ko add karte hai to result ek integer hi ata hai) |
Integers are closed under addition. |
| Subtraction | 8−8=0, is an integer 6−9=−3, which is an integer. In general, a−b is an integer for any two integers a and b. (Bachcho hum dekh sakte hai ki jab hum kisi bhi 2 integers ko subtract karte hai to result ek integer hi ata hai) |
Integers are closed under subtraction. |
| Multiplication | 0×5=0, is an integer 8×6=48, which is an integer. In general, for any two integers a and b, a×b is also an integer. (Bachcho hum dekh sakte hai ki jab hum kisi 2 integers ko multiply karte hai to result mein hume ek integer hi milta hai aur yhi reason hai ki integers closure property show karte hai multiplication ke lie) |
Integers are closed under multiplication. |
| Division | 4÷5=45, which is not an integer while if we divide 6 by 2, then we get 3, which is an integer. (Bachcho isse hum kah sakte hai ki sare integers ke lie ye true nhi hai ki jab hum unko divide kare to result mein hume ek integer hi mile) |
Integers are not closed under division. |
Rational Numbers
| Operations | Numbers | Remarks |
|---|---|---|
| Addition | −83+73=−8+73=−13, is a rational number −35+47=−21+2035=−135, which is a rational number. We find that for any two rational numbers ab and cd, ab+cd is also a rational number. (Bachcho hum dekh sakte hai ki chahey hum kisi bhi 2 rational numbers ko add karle, result mein hume humesha ek rational number hi milta hai) |
Rational numbers are closed under addition. |
| Subtraction | 35−47=21−2035=135, is a rational number −57−23=−15−1421=−2921, which is a rational number. We find that for any two rational numbers ab and cd, (ab)–(cd) is also a rational number. (Bachcho apne notice kiya hoga ki, kisi bhi 2 rational number ko subtract karne se hume result mei ek rational number hi milta hai) |
Rational numbers are closed under subtraction. |
| Multiplication | (−23)×(45)=−815, is a rational number. We find that for any two rational numbers ab and cd, ab×cd is also a rational number. (Bachcho kisi bhi do rational number ko multiply karne se result mein hume ek rational number hi milta hai) | Rational numbers are closed under multiplication. |
| Division | −43÷54=−1615, which is a rational number. We find that for any rational number ab, ab÷0 is not defined. (Bachcho hum dekh sakte hai ki kisi bhi do rational numbers ko divide karne par result mein hume humesha ek rational number hi milta hai except for when the divisor rational number is 0 kyonki tab hume result mein ∞ milta hai jo ki ek rational number nhi hai) |
Rational numbers are not closed under division. However, if we exclude zero then the collection of, all other rational numbers is closed under division |
Commutativity : A set of number is said to be commutative for a specific mathematical operation if the result obtained when changing order of the operands does not change the result.
Bachcho iska mtlb ye hai ki agar hum kisi numbers ke collection mein koi mathematical operation yani addition, subtraction, multiplication ya division apply karte hai to jo result ayega hume usse next step mein check karna hai uss result se jo un numbers ki place ko interchange karne se ayega (with same operation). Agar wo result same ata hai to wo set commutative property show karega for that mathematical operation.
Whole Number
| Operations | Numbers | Remarks |
|---|---|---|
| Addition | 0+8=8+0=8 9+8=8+9=17 We find that, for any two whole numbers a and b, a+b=b+a (Bachcho hum dekh sakte hai ki kisi bhi 2 whole numbers ko add karne par result same ata hai agar hum un numbers ki place ko interchange karde tab bhi) |
Addition is commutative. |
| Subtraction | 5−3=2 but 3−5=−2. So, 5−3≠3−5. We find that, for any two whole numbers a and b, a−b≠b−a. (Bachcho hum dekh sakte hai ki kisi bhi 2 whole numbers ko subtract karne par jo result ata hai wo same nhi hota uss result ke jo ki un numbers ki place ko interchange karne se mila, jaisa ki apne upar dekha jab humne 3 ko 5 se subtract kiya tab 2 aya jabki 5 ko 3 se subtract karne par result −2 aya) |
Subtraction is not commutative. |
| Multiplication | 3×5=5×3=15 We find that, for any two whole numbers a and b, a×b=b×a (Bachcho chahey hum 2 whole numbers ko kaise bhi multiply kyon na karle result same hi ata hai) |
Multiplication is commutative. |
| Division | (3÷5)≠(5÷3) and (6÷3)≠(3÷6). We find that, for any two whole numbers a and b, ab≠ba (Bachcho humne ye dekha ki jab bhi hum kisi do integers ko divide karte hai tab result same nhi ata agar hum un integers ki place ko interchange karde mtlb ki agar hum 6 ko 3 se divide kar rhey hai to result same nhi ayega agar hum 3 ko 6 se divide karenge) |
Division is not commutative. |
Integers
| Operation | Numbers | Remarks |
|---|---|---|
| Addition | −1+5=5+(−1)=4, is an integer. We find that, for any two integers a and b, a+b=b+a. (Bachcho hum dekh sakte hai ki hum integers ko kaise bhi add karle result humesha same aata hai) |
Addition is commutative. |
| Subtraction | −1−5=−6 and 5−(−1)=6⇒−1−5≠5−(−1). We find that, for any two integers a and b, a−b≠b−a. (Bachcho hum dekh sakte hai ki 2 integers ke subtraction ka result same nhi ata agar hum un integers ke place ko interchange karde jaise 5−3 is 2 while 3−5 is −2) |
Subtraction is not commutative. |
| Multiplication | −1×(5)=5×(−1)=−5. We find that, for any two integers a and b, a×b=b×a. (Bachcho hum do integers ko kaise bhi multiply karle result humesha same hi ata hai as you can see above) |
Multiplication is commutative. |
| Division | (−1)÷5=−0.2 and 5÷(−1)=−5 ⇒−1÷5≠5−1. We find that, for any two integers a and b, a÷b≠b÷a. (Bachcho hum dekh sakte hai ki jab hum 2 integers ko divide karte hai tab jo result ata hai wo same nhi hota, agar hum un integers ki place ko interchange kardete hai aur isi wajh se integers are not commutative under division) |
Division is not commutative. |
Rational Numbers
| Operation | Numbers | Remarks |
|---|---|---|
| Addition | −65+(−83)=−5815=(−83)+(−65). We can say that for any two rational numbers ab and cd, ab+cd=cd+ab. (Bachcho hum dekh sakte hai ki 2 rational numbers ke sum ka result humesha same ata hai chahey hum unhey kaise bhi add karle) |
Addition is commutative. |
| Subtraction | 23−54=−712 and 54−23=712 ⇒(23−54)≠(54−23). We find that, for any two rational numbers ab and cd, ab−cd≠cd−ab. (Bachcho hum dekh sakte hai ki 2 rational number ka subtraction ka result unhi rational numbers ke interchange ke subtraction ke result ke equal nhi hota) |
Subtraction is not commutative. |
| Multiplication | −43×54=−53=54×−43. So, we can say that, for any two rational numbers ab and cd, ab×cd=ab×cd. (Bachcho apne notice kiya hoga ki 2 rational numbers multiplication ka result same rhta hai chahey hum unke place ko interchange kyon na karde) |
Multiplication is commutative. |
| Division | (−53)÷(43)≠(43)÷(−53). We can say that, for any two rational numbers a and b, ab≠ba. (Bachcho aap dekh sakte ho ki 2 rational number ke division ka result unke interchange ke division ke result ke equal nhi hota as you can see above) |
Division is not commutative. |
Associativity : A set of numbers is said to be associative for a specific mathematical operation if the result obtained when changing grouping (parenthesizing) of the operands doesn't change the result.
Bachcho iska mtlb ye hai ki agar hum ek numbers ke collection mein koi mathematical operation yani addition, subtraction, multiplication ya division apply karte hai to jo result ayega usse hume next step mein unhi numbers ki grouping change(with same operation) karne ke baad jo result ayega usse check karna hai. Agar result same ata hai to wo set associative property show karega otherwise nhi for that mathematical operation.
Whole Numbers
| Operation | Numbers | Remarks |
|---|---|---|
| Addition | 5+(3+2)=10=(5+3)+2 For any three whole numbers a,b and c, a+(b+c)=(a+b)+c (Bachcho hum dekh sakte hai ki yha humare paas whole numbers ka collection {5,3,2} hai aur jab humne 3 aur 2 ko add kiya aur uske result ko 5 se add kiya tab hume whi result mila jo ki hume tab mila tha jab humne pahle 5 aur 3 ko add kiya then uss result ko 2 se, yhi wajh hai ki whole numbers are associative under addition) |
Addition is associative. |
| Subtraction | 5−(3−2)=4 and (5−3)−2=0⇒5−(3−2)≠(5−3)−2. For any three whole numbers a,b and c, a−(b−c)≠(a−b)−c (Bachcho hum dekh sakte hai ki agar hum pahle 2 ko 3 se subtract karte and then uss result ko 5 se subtract karte hai to hume wo result nhi mila jo ki hume tab mila tha jab humne pahle 3 ko 5 se subtract kiya then uss result mein se 2 ko aur yhi reason hai ki whole numbers are not associative under subtraction) |
Subtraction is not associative. |
| Multiplication | 3×(2×4)=24=(3×2)×4 For any three whole numbers a,b and c a×(b×c)=(a×b)×c (Bachcho aap dekh sakte ho ki hum whole numbers ke collection ko kisi bhi order mei multiply kyon na karle result humesha same aata hai) |
Multiplication is associative. |
| Division | 10÷(4÷2)=5 and (10÷4)÷2=1.25⇒10÷(4÷2)≠(10÷4)÷2. For any three whole numbers a,b and c a÷(b÷c)≠(a÷b)÷c (Bachcho yha pe jab humne pahle 4 ko 2 se divide kiya and then uss result se 10 ko tab hume wo result nhi mila jo ki hume tab mila tha jab humne pahle 10 ko 4 se and then then uss result ko 2 se divide kiya) |
Division is not associative. |
Integers
| Operation | Numbers | Remarks |
|---|---|---|
| Addition | 2+[3+(−4)]=1=[2+3]+(−4) For any three integers a,b and c, a+(b+c)=(a+b)+c (Bachcho yha humare paas ek integers ka collection {2,3,−4} hai aur jab humne 3 aur −4 ko add kiya and then uss result ko 2 se add kiya tab hume whi result mila jo ki hume tab mila jab humne 2 aur 3 ko pahle add kiya and then uss result ko −4 se add kiya aur yhi reason hai ki integers are associative under addition) |
Addition is associative. |
| Subtraction | 8−[3−(−2)]=3 and [8−3]−(−2)=7⇒8−[3−(−2)]≠[8−3]−(−2) For any three integers a,b and c, a−(b−c)≠(a−b)−c (Bachcho yha pe jab humne −2 ko 3 se subtract kiya and then uss result ko 8 se subtract kiya tab hume wo result nhi mila jo ki hume tab mila tha jab humne pahle 3 ko 8 se subtract kiya and then uss result mein se −2 ko) |
Subtraction is not associative. |
| Multiplication | 2×[3×1]=6=[2×3]×1 For any three integers a,b and c a×(b×c)=(a×b)×c (Bachcho aap yha dek sakte ho ki hum integers ke collection ko chahey kisi bhi order mein multiply kare result humesha same hi ata hai) |
Multiplication is associative. |
| Division | 10÷[4÷2]=5 and [10÷4]÷2=1.25⇒10÷[4÷2]≠[10÷4]÷2 For any three integers a, b and c a÷(b÷c)≠(a÷b)÷c (Bachcho yha par jab humne 4 ko 2 se and then uske result se 10 ko divide kiya tab hume wo result nhi mila jo ki hume tab mila tha jab humne 4 se 10 ko divide kiya and then uske result ko 2 se divide kiya, yhi reason hai ki integers are not associative under division) |
Division is not associative. |
Rational Numbers
| Operation | Numbers | Remarks |
|---|---|---|
| Addition | −23+[35+(−56)]=−23+(−730)=−910 [−23+35]+(−56)=−115+(−56)=−910 So, −23+[35+(−56)]=[−23+35]+(−56) For any three rational numbers ab,cd and ef, ab+(cd+ef)=(ab+cd)+ef (Bachcho humare paas yha rational numbers ka collection {−23,35,−56} hai aur jab humne 35 aur −56 ko add kiya and then uske result ko −23 se add kiya tab hume whi result mila jo ki hume tab mila tha jab humne pahle −23 aur 35 ko add kiya and then uske result ko −56 se add kiya aur yhi reason hai ki rational numbers are associative under addition) |
Addition is associative. |
| Subtraction | 54−[311−(−47)]≠[54−311]−(−47) For any three rational numbers ab,cd and ef, ab−(cd−ef)≠(ab−cd)−ef (Bachcho yha par jab humne pahle 311 se −47 ko subtract kiya and then uss result ko 54 se subtract kiya tab hume wo result nhi mila jo ki hume tab mila jab humne pahle 54 se 311 ko subtract kiya and then result mein se −47 ko subtract kiya, yhi reason hai ki rational numbers are not associative under subtraction) |
Subtraction is not associative. |
| Multiplication | 23×[45×72]=2815=[23×45]×72 For any three rational numbers ab,cd and ef ab×((cd)×ef)=(ab×cd)×ef (Bachcho hum rational numbers ke collection ko chahey kisi bhi order mein multiply kare, result humesha same milta hai) |
Multiplication is associative. |
| Division | 43÷[23÷−67]≠[43÷23]÷−67 For any three rational numbers ab, cd and ef, ab÷(cd÷ef)≠(ab÷cd)÷ef (Bachcho yha par jab humne 23 ko −67 se divide kiya and then uss result se 43 ko divide kiya tab hume wo result nhi mila jo ki hume tab mila tha jab humne pahle 43 ko 23 se divide kiya and then uss result ko −67 se divide kiya aur yhi reason hai ki rational number are not associative under division) |
Division is not associative. |
Definition 1
Additive identity is a number, which when added to any number, gives the sum as the number itself.
The role of zero {0}
Bachcho additive identity ka mtlb ye hai ki ek aisa number ho jise kisi bhi number mein add karne se given number mein koi change na aye. Aur jaisa ki aap sab jante ho ki aisa sirf ek hi number exist karta hai jisse kisi bhi number mein add kare to uss number mein ko change nhi ata and that is 0.
Bachcho yhi reason hai ki hum isko role of zero {0} topic ke naam se padhte hai.
Let's see.
3+0=0+3=3 [Addition of 0 to a whole number]
−7+0=0+(−7)=−7 [Addition of 0 to an integer]
54+0=0+54=54 [Addition of 0 to a rational number]
Bachcho abhi apne dekha ki jab hume whole number, integer aur rational number mein 0 ko add kiya to unme koi change nhi aya.
Isse hum kah sakte hai ki rational numbers, integers aur whole numbers ke lie 0 additive identity hai.
Definition 2
According to the multiplicative identity, any number multiplied by 1, gives the same result as the number itself.
The role of one {1}
Bachcho multiplicative identity ka mtlb ye hai ki agar hum kisi bhi number ko 1 se multiply karenge to usme koi change nhi ayega.
Let's see.
2×1=1×2=2 [Multiplication of 1 with a whole number]
(−7)×1=1×(−7)=−7 [Multiplication of 1 with a integer]
23×1=1×23=23 [Multiplication of 1 with a rational number]
Bachcho abhi aap sabne dekha ki jab humne 1 se whole number, integer aur rational number ko multiply kiya tab unme koi change nhi aya.
Isse hum kah sakte hai ki rational numbers, integers aur whole numbers ke lie 1 multiplicative identity hai.
Definition 3
The additive inverse of a number a is the number that, when added to a, yields zero. This number is also known as the opposite, sign change, and negation.
Negative of a number
Bachcho kisi bhi number a ke lie wo number additive inverse kahlata hai jisse usme add karne par result zero aye. Aur jaisa ki aap jante ho ki aisa tabhi possible hai agar hum a ka sign change karke usme add karde.
Let's see.
For a whole number 2 we have,
2+(−2)=0 [Here additive inverse for 2 is −2.]
For an integer −2, we have
−2+2=0 [Here 2 is the additive inverse for integer −2.]
For a rational number −57, we have
−57+57=0 [Here 57 is the additive inverse for rational number −57]
In general, for a rational number ab, we have ab+(−ab)=(−ab)+ab=0. We can say that −ab is the additive inverse of ab and ab is the additive inverse of (−ab).
Definition 4
Multiplicative inverse or reciprocal for a number x, denoted by 1x or x⁻¹, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction ab is ba.
Reciprocal
Bachcho asaan bhasha mein multiplicative inverse ka ye mtlb hai ki agar hume koi number given hai x to agar hum usme uska reciprocal 1x multiply karenge to result 1 ayega aur uska reciprocal hi
uss number ke lie multiplicative inverse kahlayega.
Let's see.
For a rational number 817, we have
817×178=1 [Here 178 is the reciprocal of rational number 817.]
Bachcho aap sab jante ho ki 0 ko hum rational number ki form mein represent kar sakte hai magar aisa koi number exist nhi karta jisse 0 se multiply karne se result 1 aye kyonki agar hum kisi bhi number ko 0 se multiply karenge to result 0 ata hai. So, we can conclude that 0 has no reciprocal.
Distributive property of multiplication over addition and subtraction for rational numbers
The distributive property of multiplication is :
Over Addition : a(b+c)=ab+ac
Isse hum ek example se samjhte hai jisme hume rational numbers given hai 23, 54 and −34.
23×{54+(−34)}=23×12=13 ...(i)
(23×54)+(23×−34)=56−12=5−36=13 ...(ii)
From (i) and (ii), we get
23×{54+(−34)}=(23×54)+(23×−34)
Over Subtraction : a(b−c)=ab−ac
Isse hum ek example se samjhte hai jisme hume rational numbers given hai 23, 54 and −34.
23×{54−(−34)}=23×2=43 ...(i)
(23×54)−(23×−34)=56+12=43 ...(ii)
From (i) and (ii), we get
23×{54−(−34)}=(23×54)−(23×−34)
Note : When you use distributivity, you split a product as a sum or difference of two products.
Example 1
Express −3344 in standard form.
We can see that given number is a rational number.
−3344=−1×11×311×4=−34
Standard form of −3344 is −34.
Example 2
Verify that : (i)23×[67×−415]=[23×67]×−1415
(ii)56×[−45+(−710)]=[56×−45]+[56×−710]
(i) We have,
LHS:23×[67×−415]=23×[−835]=−16105
RHS:[23×67]×−1415=[47]×−1415=−815≠LHS.
Hence this is not true.
(ii) We have,
LHS:56×[−45+(−710)]=56×[−1510]=−54
RHS:[56×−45]+[56×−710]=[−23]+[−712]=−1512=−54=LHS
Hence verified.
Example 3
Find the additive inverse of :
(i)59 (ii)−911
(i) Additive inverse of 59 is −59 because (59)+(−59)=0.
(ii) Additive inverse of −911 is 911 because (−911)+(911)=0.
Example 4
Find the reciprocal of each of the following :
(i)56
(ii)−1417
We know that, for a rational number ab reciprocal will be cd if ab×cd=1, so
(i)56×cd=1⇒cd=156=65
(ii)−1417×cd=1⇒cd=1−1417=−1714
Example 5
Representation of Rational Numbers on the Number Line
Bachcho apne pichli classes mein natural numbers, whole numbers aur integers ko number line mein represent karna sikha tha lekin ab hum rational numbers ko number line mein represent karna sikhenge.
(i) Natural Numbers
Bachcho natural numbers ke lie number line 1 ke right hand side mein indefinitely extend karta hai.
(ii) Whole number
The line extends indefinitely to the right, but from 0. There are no numbers to the left of 0 kyonki aap sab jante hai ki whole numbers 0 se start hote hai.
(iii) Integers
The line extends indefinitely on both sides
kyonki aap sab jante ho ki integers mein negative numbers aur whole numbers included hai.
(iv) Rational Numbers
Bachcho aap jante ho ki rational number wo numbers hote hai jinhe hum pq (p and q are integers and q≠0) ki form mein represent kar sakte hai. Hum inhe number line mein easily represent kar sakte hai lekin usse pahle hum 2 points dekhenge jo niche mentioned hai.
1. Represent 34 on the number line.
Soln. Yha rational no. positive hai islie isse number line mein 0 ke right side mein represent kiya jayega aur denominator ki value 4 hai, so sabse pahle hum 0 se 1 ko 4 equal parts mein divide kar denge. Un 4 parts mein se 3rd part 34 ko represent karega.
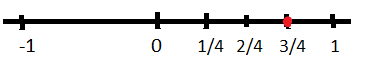
2. Represent −35 on the number line.
Soln. Yha aap dekh sakte ho ki rational no. ki value 0 se chhoti aur −1 se badi hogi kyonki sign negative aur num. value deno. value se chhoti hai. Isse number line mein represent karne ke lie hum 0 se −1 ko 5 equal parts mein divide kardenge kyonki deno. value 5 hai aur un fifth parts mein se 3rd part −35 ko represent karega.
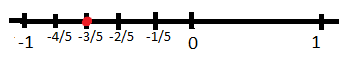
Chalo isse example se samjhte hai.
1. Represent 95 on the number line.
Soln. Bachcho yha given rational number ki value 1 se badi hogi kyonki num. value deno. value se badi hai aur ye +ve hai islie origin ke right side mein represent kiya jayega. Sabse pahle hum 95 ko mixed fraction mein change karenge jisse hume 145 mila i.e., rational number lie between 1 and 2. Ab hum 1 aur 2 ke beech mein number line ko 5 equal parts mein divide karenge jisme fourth part required rational number ko number line mein represent karega.
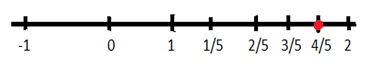
Rational Numbers between Two Rational Numbers
Bachcho agar mai apse puchu ki 6 aur 9 ke beech ke natural numbers batao to apka answer hoga 7 aur 8.
Whole numbers between 9 and 11 is 10.
Integers between −1 and 3 are 0,1, and 2.
Isse hum kah sakte hai ki kisi bhi 2 integers, whole numbers aur natural numbers ke beech mein definite numbers exist karte hai.
Lekin kya hoga agar koi apse 2 rational numbers ke beech ke rational numbers nikalne ke lie kahe. Chalo ab hum isse sikhte hai.
How many rational numbers are there between 310 and 710 ?
Apne socha hoga ki 410,510 and 610. Lekin kya hum 310 ko 30100 aur 710 ko 70100 nhi likh sakte ? Answer is yes we can. To iska mtlb hai 31100,32100,...,69100 numbers lie karte hai 310 aur 710 ke beech mein.
Hum 310 ko 3001000 aur 710 ko 7001000 bhi likh sakte hai jiska mtlb hai ki 3011000,3021000,...,6991000 numbers lie karte hai 310 aur 710 ke beech mein and so on.
Apne notice kiya hoga ki two rational numbers ke beech mein countless rational numbers lie karte hai.
Note : Between any 2 numbers, it is not necessary that there will be a natural number, whole number or integer but there is always a rational number.
Example 6
Find five rational numbers between 35 and 45.
Since the numbers have same denominator and we have to find 5 rational numbers between 35 and 45.
Since we have to find 5 rational numbers, we multiply the numbers by 66.
35=35×66=1830
45=45×66=2430
Thus 5 rational numbers 35 and 45 are
1930,2030,2130,2230,2330.
Example 7
Represent these numbers on the number line.
(i)74 (ii)−56
(i) Firstly we will convert 74 into mixed fraction and that is 134. From the mixed fraction we came to know that the given rational number lies between 1 and 2 on the number line. Then we will divide the number line between 1 and 2 into 4 equal parts [because denominator is 4] in which 3rd part from 1 represent the given rational number.
(ii) Given rational number is negative so it is represented on the left side of origin between 0 and −1 because here numerator is less than denominator and sign is negative. Then we will divide the number line between 0 and −1 into 6 equal parts in which the fifth parts from the origin represents the given rational number.
Example 8
The product of two numbers is −2827. If one of the numbers is −49, find the other.
Let the other rational number be x, then
(x)×−49=−2827
⇒x=−2827−49=−2827×−94=252108=73
The required answer is 73.
Example 9
Arrange the numbers −35,−710 and −58 in ascending order.
To arrange the given numbers in ascending order we have to first make the denominator same [which could be done by taking LCM of denominators of given numbers] of all given rational numbers. So, −35,−710 and −58 can be written as
−35=−2440;−710=−2840;−58=−2540
Now we can arrange all those numbers easily and that is −2440>−2540>−2840. So the required answer is −35>−58>−710.
Example 10
The sum of two rational numbers is −5. If one of them is −136, find the other.
Let the other rational number be x. So according to given question,
x+−136=−5
⇒x=−5+136=−176
Required answer is −176.
Example 11
Summary
1. Rational numbers are closed under the operations of addition, subtraction and multiplication.
2. The operations addition and multiplication are
(i) commutative for rational numbers.
(ii) associative for rational numbers.
3. The rational number 0 is the additive identity for rational numbers.
4. The rational number 1 is the multiplicative identity for rational numbers.
5. The additive inverse of the rational number ab is −ab and vice versa.
6. The reciprocal or multiplicative inverse of the rational number ab is cd if ab×cd=1.
7. Distributivity of rational numbers: For all rational numbers a, b and c
a(b+c)=ab+ac and a(b–c)=ab–ac
8. Rational numbers can be represented on a number line.
9. Between any two given rational numbers there are countless rational numbers. The idea of mean
helps us to find rational numbers between two rational numbers.
Let's Revise
- Rational numbers are those which can be represented in the form of pq where p and q are integers and q≠0.
- Rational numbers are closed under addition, subtraction and multiplication but not under division (but if we exclude 0 it is)
- Rational numbers are commutative under addition and multiplication but not under subtraction and division.
- Rational numbers are associative under addition and multiplication but not under subtraction and division.
- The rational number 0 is the additive identity for rational numbers.
- The rational number 1 is the multiplicative identity for rational numbers.
- The additive inverse of the rational number ab is −ab and vice versa.
- The reciprocal or multiplicative inverse of the rational number ab is cd if ab×cd=1.
0 has no reciprocal. - a(b+c)=ab+ac
- a(b−c)=ab−ac
- There are indefinite number of rational numbers between two rational number.
- We can represent rational numbers on the number line but for that we need to know that which type of fraction was that proper fraction or improper fraction.