PRACTICAL GEOMETRY for Class 8 MATHS
INTRODUCTION
Bachcho apne pichli class mein triangle ko draw karna sikha tha aur apne ye bhi dekha tha ki ek unique triangle ko draw karne ke lie 3 measurements (of side and angle) ki jarurat hoti hai.
To ab question ye arise hota hai ki kya ek 4 sided unique closed figure banane ke lie 4 measurements sufficient hongi ? To es chiz ko samjhne ke lie chalo hum ek experiment perform karte hai jisme humare paas 4 sticks hai jinme se 2 sticks ki length 10cm hai aur baki 2 sticks ki length 8cm hai. Agar hum unko perpendicularly join kare to hume ek rectangle ABCD milega jiski length 10cm hogi aur width 8cm. Agar hum us rectangle ko uski width ke along push karte hai to hume ek ||gm milega. Aur agar hum usi rectangle ko different direction mein push karte to hume ek different parallelogram milega jabki un 4 sticks ki measurement same rahegi. To es experiment se hum ye conclude karte hai ki ek quadrilateral banane ke lie 4 measurements sufficient nhi hai. To kya 5 measurements sufficent hongi ? Let's see.
Humare paas jo rectangle ABCD hai usme hum ek aur stick introduce karenge jiski length BD yani diagonal of rectangle ke equal hogi aur us length ko hum BD ke along tie kardenge. To ab hum ye dekh sakte hai ki rectangle ko open kiye bina hum usse push karke ek ||gm nhi bana sakte kyonki BD ye nhi hone dega i.e., 5th stick ki wajh se hume ek unique rectangle mila aur isse hum kah sakte hai ki given sides se dusra koi quadrilateral formed nhi hoga.
To ab hum ye kah sakte hai ki 5 measurements ek unique quadrilateral form kar sakte hai. Aap ye soch rhe honge ki kya 5 measurements (of sides and angles) sufficient hongi ek unique quadrilateral banane ke lie ? Hum iss chapter mein yhi sab sikhne wale hai. So let's begin our study.
Recall!
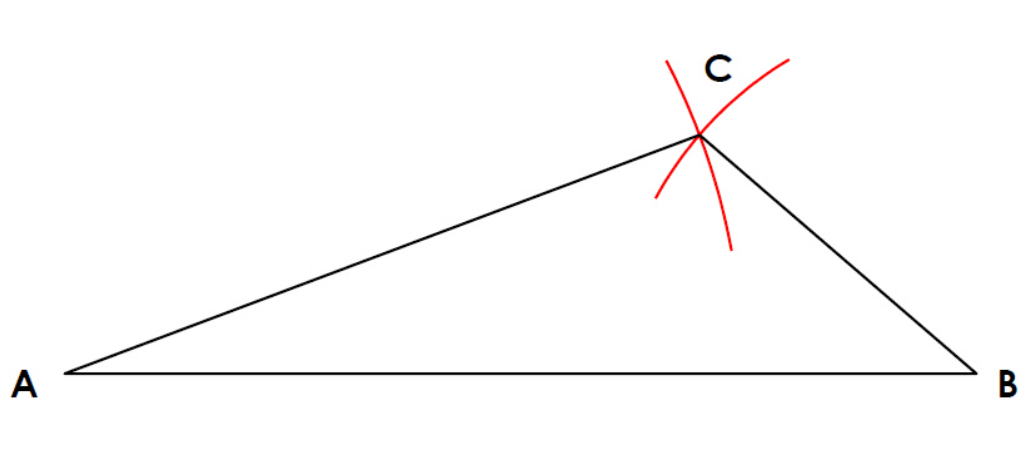
Baccho, before starting with construction of quadrilaterals, hum phle SSS construction condition se triangle kaise draw karte hai wo recall karenge.
Bachcho kisi ΔABC jiski sides, AB=x cm, BC=y cm aur CA=z cm given ho usse hum in steps se construct ya draw kar sakte hai.
In sare steps ke baad humara ΔABC hume mil jayega..
Constructing a Quadrilateral
Bachcho ab hum dekhenge ki kaise ek unique quadrilateral ko draw kiya jata hai jab 5 measurement is tarh given ho,
• When four sides and one diagonal are given.
• When two diagonals and three sides are given.
• When two adjacent sides and three angles are given.
• When three sides and two included angles are given.
• When other special properties are known.
When the lengths of four sides and a diagonal are given
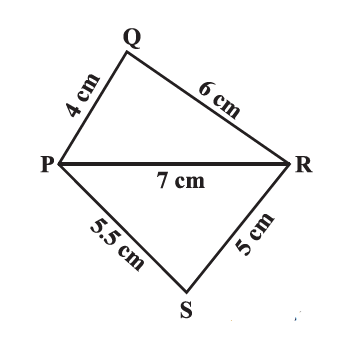
Bachcho maan lo ki hume ek quadrilateral PQRS draw karna hai where PQ=4 cm, m, QR=6 cm, RS=5 cm, PS=5.5 cm aur PR=7 cm.
Step 1 : Bachcho sabse pahle hume ek rough sketch draw karna hai jisse hum quadrilateral ko visualize kar sake aur usme hum measurements ko mark kar denge.
Baccho, hume pta hai ki har quadrilateral do triangles m divide ho skta hai. To ab hum rough figure m quadrilateral ko do triangles ki tarah visualize krenge.
Step 2 : Ab hum ΔPQR construct krke using SSS construction, jisme PQ=4cm,QR=6cm,andPR=7cm
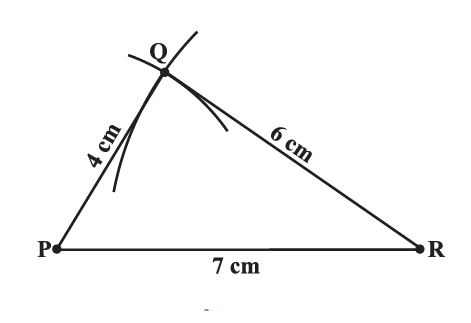
Baccho, traingle construct krne k baad hum ye dekh skte hai ki hume humare quadrilateral k three corner already mil chuke hai. Now we need the fourth corner to complete our quadrilateral.
Step 3 : Quadrilateral k fourth point (S) ko locate krne k lie hum, P and R se do arcs draw krenge. Inn dono arcs ka radius humare quadrilateral ki bachi hui dono sides k length k jitna hoga.
Because S is 5.5cm away from P, draw an arc from P of radius 5.5cm.
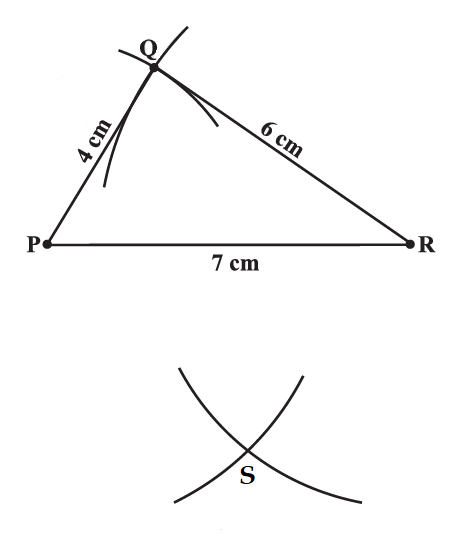
Step 5 : Similarly, kyunki Q 5cm door hai S se, we will draw an arc of radius 5cm from Q and let it cut our previous arc at point S.
Ye humare quadrilateral ka fourth point bnjaaega.
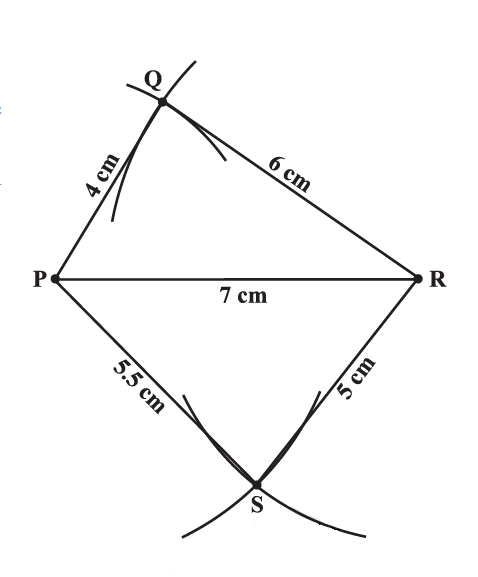
And with this, we constructed a quadrilateral when four sides and one diagonal were given.
Example `1`
Construct a quadrilateral ABCD in which AB=4.6cm, BC=2.6cm, CD=3.5cm, AD=2.6cm and the diagonal AC=4.9cm.
Step 1: Draw a line segment AB=4.6 cm.
Step 2: With A and B as the centers,draw two arcs of radii 4.9 cm and 2.6 cm respectively to intersect each other at C.
Step 3: With C and A as the centers, draw two arcs of radii 3.5 cm and 2.6 cm respectively to intersect at D.
Step 4: Join BC, CD and AD to form quadrilateral ABCD.
ABCD is the required quadrilateral.

Let's Brainstorm together!
Baccho, humne abhi seekha ki hum kaise ek quadrilateral construct kr skte hai jab hume uski four sides aur diagonal ki measurements given ho yaani ki hume in total five measurements given thi. But can you construct a parallelogram when only three of it's measurements are given? Look at the following question:
Can you draw a parallelogram BATS where BA = 5 cm, AT = 6 cm and
AS = 6.5 cm? Why?
Baccho, hum jaante hai ki parallelogram (∣∣gm) ki opposite sides equal hoti hai, to agar hume ek parallelogram ki do adjacent sides given ho, to hum baaki dono sides bhi pta laga skte hai.
∴ In the given question, since BA=5cm,andAT=6cm,
⇒ TS=BA=5cmandBS=AT=6cm
Now we have all the five measurements and we can easily construct this parallelogram. Try it out!
Baccho, ye same concept rectangles and squares m bhi apply ho skta hai. If you are given two adjacent sides of a rectangle and its diagonal, you can construct it. And if you are given one side and the diagonal of a square, you can easily construct it too kyunki square ki saari sides equal hoti hai.
When two diagonals and three sides are given
Bachcho ab hum seekhenge ki agar hume ek quadrilateral k do diagonals aur teen sides ki measurements given ho to hum use kaise construct krenge. So let's consider the following measurements:
In quadrilateral ABCD,BC=4.5cm,AD=5.5cm,CD=5cm the diagonal AC=5.5cm and diagonal BD=7cm
Step 1 : Bachcho firse hum pahle ek rough sketch draw krenge with measurements for better visualization.
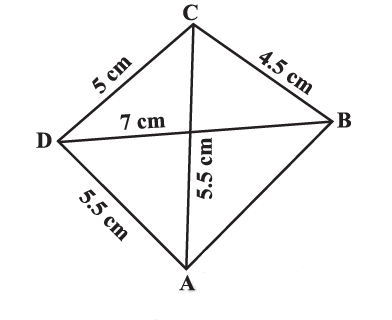
Step 2 : Ab hum △ACD construct krenge using SSS
construction, jisme AC=5.5cm,CD=5cmandAD=5.5cm
Baccho, iss triangle ko construct krne k baad ab hume quadrilateral k fourth point B locate krna hai.
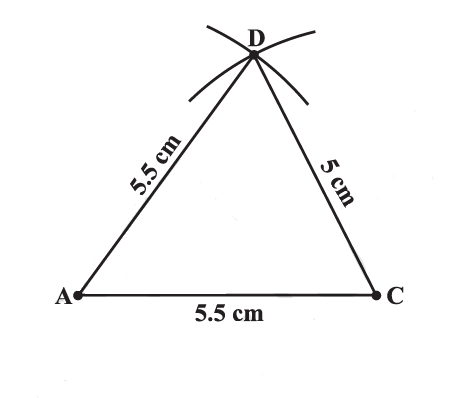
Step 3 : To locate point B, hum D ko centre lekr ek 7.7cm k radius ki arc draw krenge
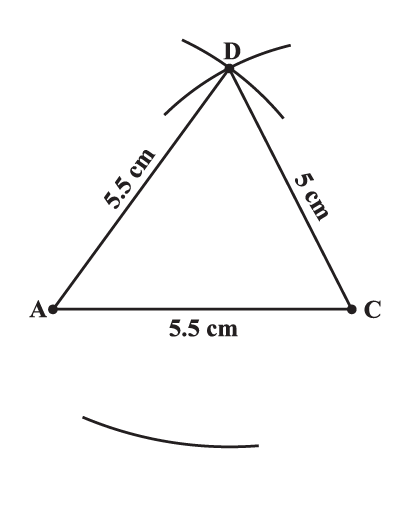
Step 4 : Baccho, kyunki hume third side BC=4.5cm given hai, hum C ko centre lekr ek 4.5cm k radius ki arc draw krenge which would cut our previous arc at B.
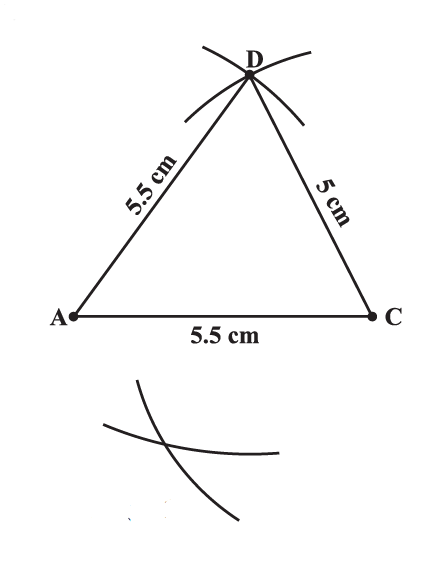
Step 5 : Join ABandBC, to complete the quadrilateral ABCD.
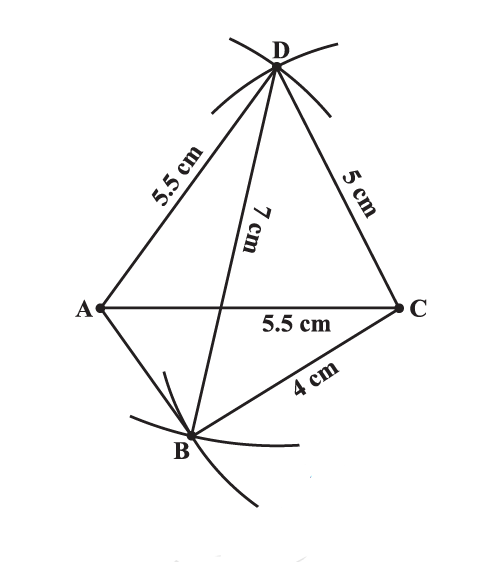
Example `2`
Construct Quadrilateral ABCD , in which
BC=4.5cm
AD=5.5cm
CD=5cm
AC=5.5cm
BD=7cm
Refer to the video for the solution.
When two adjacent sides and three angles are given
Bachcho ab hum seekhenge ki agar hume ek quadrilateral k do diagonals aur teen sides ki measurements given ho to hum use kaise construct krenge. So let's consider the following measurements:
In quadrilateral ABCD,BC=4cm,AD=5.5cm,CD=5cm the diagonal AC=5.5cm and diagonal BD=7cm
Step 1 : Bachcho firse hum pahle ek rough sketch draw krenge with measurements for better visualization.
Step 2 : Ab hum △ACD construct krenge using SSS
construction, jisme AC=5.5cm,CD=5cmandAD=5.5cm
Baccho, iss triangle ko construct krne k baad ab hume quadrilateral k fourth point B locate krna hai.

Step 3 : To locate point B, hum D ko centre lekr ek 7cm k radius ki arc draw krenge

Step 4 : Baccho, kyunki hume third side BC=4cm given hai, hum C ko centre lekr ek 4cm k radius ki arc draw krenge which would cut our previous arc at B.

Step 5 : Join ABandBC, to complete the quadrilateral ABCD.

Example `3`
Construct a quadrilateral ABCD , where AB=3.5cm,BC=6.5cm,∠A=750,∠B=1050and∠C=1200
Refer to the video for the solution.
When three sides and two included angles are given
Bachcho ab hum seekhenge ki agar hume three sides aur two included angles given ho to hum ek quadrilateral kaise construct krskte hai. Let;s consider the following question :
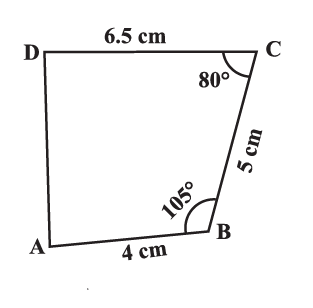
Construct a quadrilateral ABCD, where
AB=4cm,BC=5cm,CD=6.5cmand∠DB=105°and∠DC=80°.
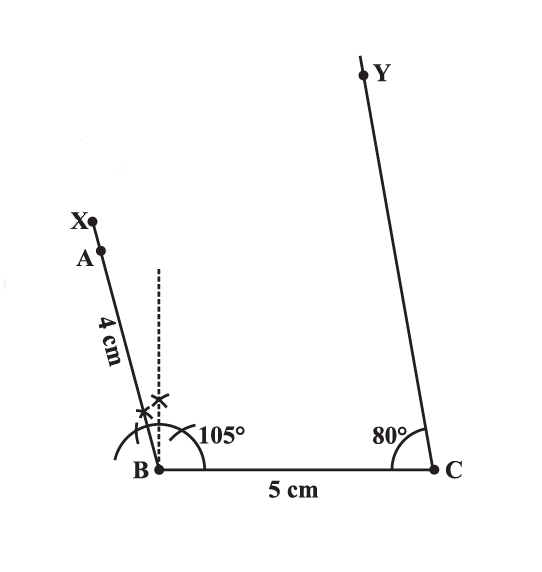
Step 1 : Hum sabse phle ek rough figure bnaaenge and saari measurements clearly mark krlenge.
Step 2 : Baccho, we'll draw a line segment BC of length 5cm. Uske baad we'll construct an angle ∠CBX=105° On ray BX, mark A at a distance of 4cm away from B. Now, we have three corners of the quadrilateral (A,B,C).
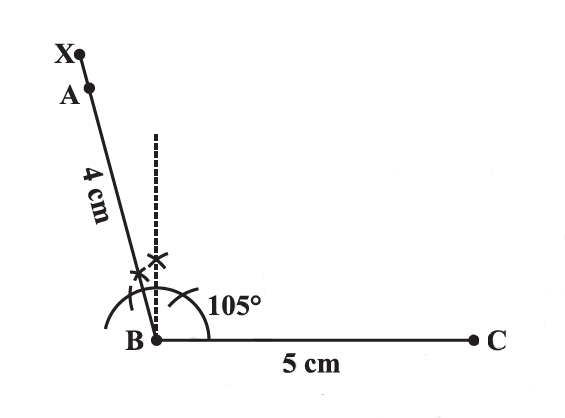
Step 3 : Fourth point D ko locate krne k lie, hum point C par ∠BCY=80° construct krenge.
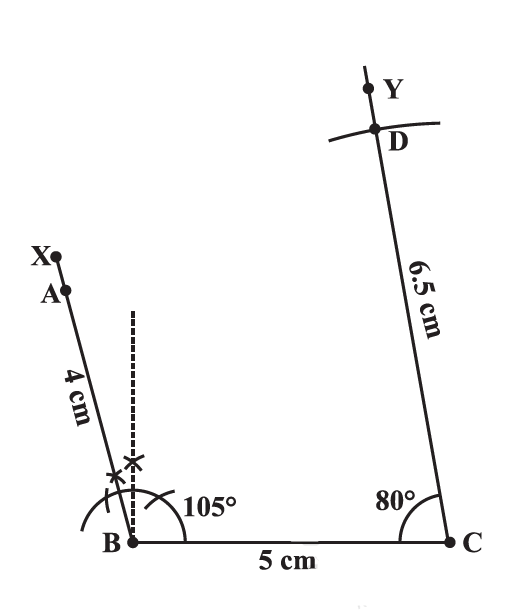
Step 4 : Now, on ray CY, we'll mark D at a distance of 6.5cm away from C.
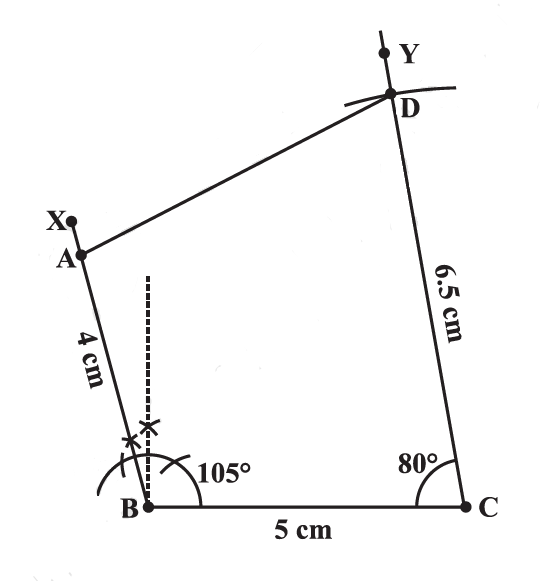
Step 5 : Join A and D to get the fourth side of the quadrilateral ABCD.
Example `4`
Construct a quadrilateral PQRS, in which ∠Q=450,∠R=900,QR=5cm,PQ=9cmandRS=7cm
Refer to the video for the solution.
When other special properties are known
Baccho now we'll consider some special cases of constructing quadrilaterals. Before starting let us revise the different types of quadrilaterals.
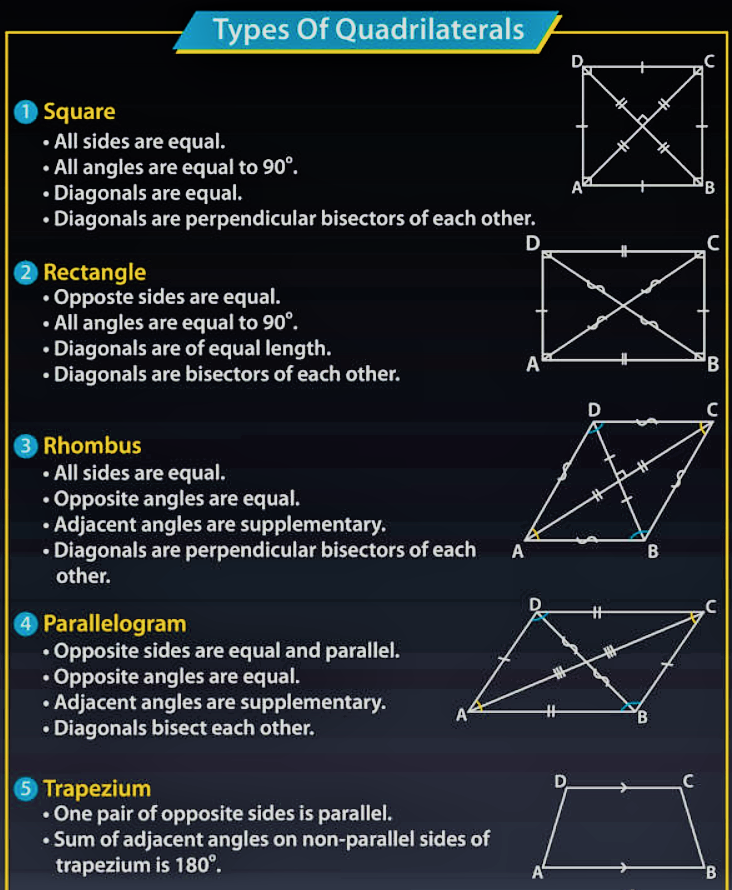
Baccho, abhi tk humne dekha ki we were given various measurements of sides and angles of the quadrilateral. But what if we're given only a few measurements of a specific quadrilateral? Let's consider the following examples :
1) Draw a square ABCD of side 4.5 cm.
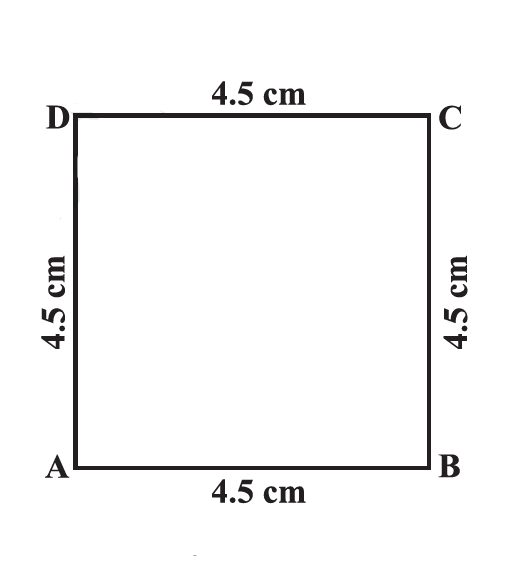
Baccho, as you can see, we're given only one measurement but also, we are given that the quadrilateral is a square and we know that a square has all its sides equal and all its angles equal to 90°. So let's see how to construct it!
Step 1 : Draw a line segment AB of length 4.5cm.
Step 2 : At B, construct an angle equal to 90°. On the other arm of the angle, mark C at a distance of 4.5cm away from B. Baccho, jab aap AandC ko join krenge, you'll see that you have got a △ABC using SAS rule.
Step 3 : Baccho ab aap easily point D locate kr skte hai by drawing two arcs of radii 4.5cm from points AandC.
Step 4 : Join all the points and you'll have a square ABCD.
2) Construct a rhombus ABCD where AC=6cmandBD=7cm
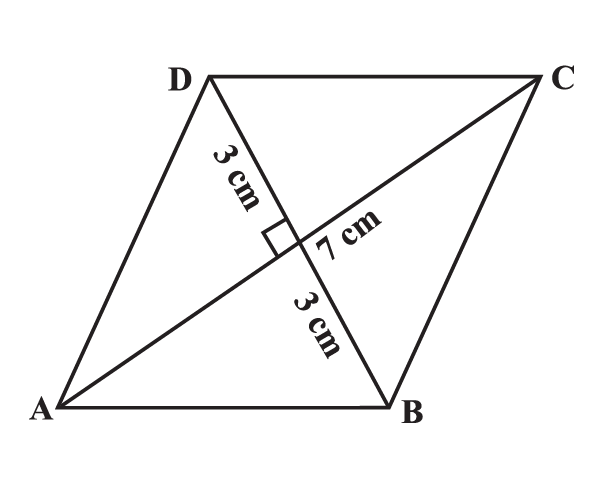
Baccho, iss case m bhi hume sirf rhombus k dono diagonals given hai. We are not given any measurements of sides or its angles, so how will we construct it? We know that ABCD is a rhombus and rhombus ki saari sides equal hoti hai and the diagonals of a rhombus are perpendicular bisectors of each other!. So let's construct this :
Step 1 : Draw a line segment BD=7cm.
Step 2 : Baccho, ab hum BD ka perpendicular bisector construct krenge.
Step 3 : To get our other diagonal, we'll cut the perpendicular bisector with an arc of radius 3cm(62) on either sides of BD and we'll mark both the points as A and C. Isse hume humara dusra diagonal AC miljaaega.
Step 4 : Join the end points of both the diagonals (A,B,CandD) to get rhombus ABCD.
Example `5`
Construct a square of side 3cm.
Steps:
1. Draw a line segment PQ=3cm.
2. Construct ∠PQX=90∘.
3. Mark the point R on −−→QX such that QR=3cm.
4.With R and P as centres and with radii of 3cm each , draw two arcs to intersect each other at S.
5. Join PS and RS to form the required square PQRS.

Let's Summarize
- Five measurements can determine a quadrilateral uniquely.
- A quadrilateral can be constructed uniquely if the lengths of its four sides and a diagonal is given.
- A quadrilateral can be constructed uniquely if its two diagonals and three sides are known.
- A quadrilateral can be constructed uniquely if its two adjacent sides and three angles are known.
- A quadrilateral can be constructed uniquely if its three sides and two included angles are given.
Let's Revise
1) Baccho iss chapter m humne seekha ki ek unique quadrilateral ko bnane k lie five measurements ki zaroorat pdhti hai. We learnt how to construct different quadrilaterals jisme kahi p sides aur kahi p angles k measurements given hote hai using only compass and ruler.
2) Humne seekha ki agar kisi quadrilateral ki four sides aur ek diagonal ka measurement given ho to hum kaise use construct kr skte hai by constructing a triangle first using SSS construction condition.
3) We also learnt the construction of a quadrilateral jiski hume sirf teen sides aur do diagonals ki measurements given ho.
4) Then we learnt about the construction of a quadrilateral where we are given its two adjacent sides and three angles.
5) Fir humne seekha ki agar ek quadrilateral ki sirf teen sides aur do included angles given ho to use kaise construct kia jaata hai.
6) Finally, we revised our types of quadrilaterals and learnt special cases where only a few of the details are given.