PLAYING WITH NUMBERS for Class 8 MATHS

Baccho, aaj hum "Playing with numbers" chapter pdhenge. Baacho, aapne apni previous classes m number system aur types of numbers k baare m pdha hua hai like integers, natural numbers, etc. Iss chapter m hum inn numbers se related aur cheezein explore krenge based on their interesting properties and rules. We will also learn justifications of various divisibility rules that we have learnt in our previous classes. So let's begin!

Baccho. numbers ko general form m likhna is similar to writing numbers in expanded form. Aapne apni previous classes m place values k baare m pdha aur aap jaante hai ki har number k har digit ki ek place value hoti hai which starts with ones, tens, hundreds, thousands and so on starting from rightmost digit.
Expanded form is useful to split and present the higher digit number in its units, tens, hundreds, thousands form. An expanded form helps to better understand and rightly read the higher digit numbers. A number of the form $10,030$, is sometimes difficult to understand directly and can be represented in expanded form as $10030=10,000+30$.
Some more examples of the expanded form are provided in the following table.

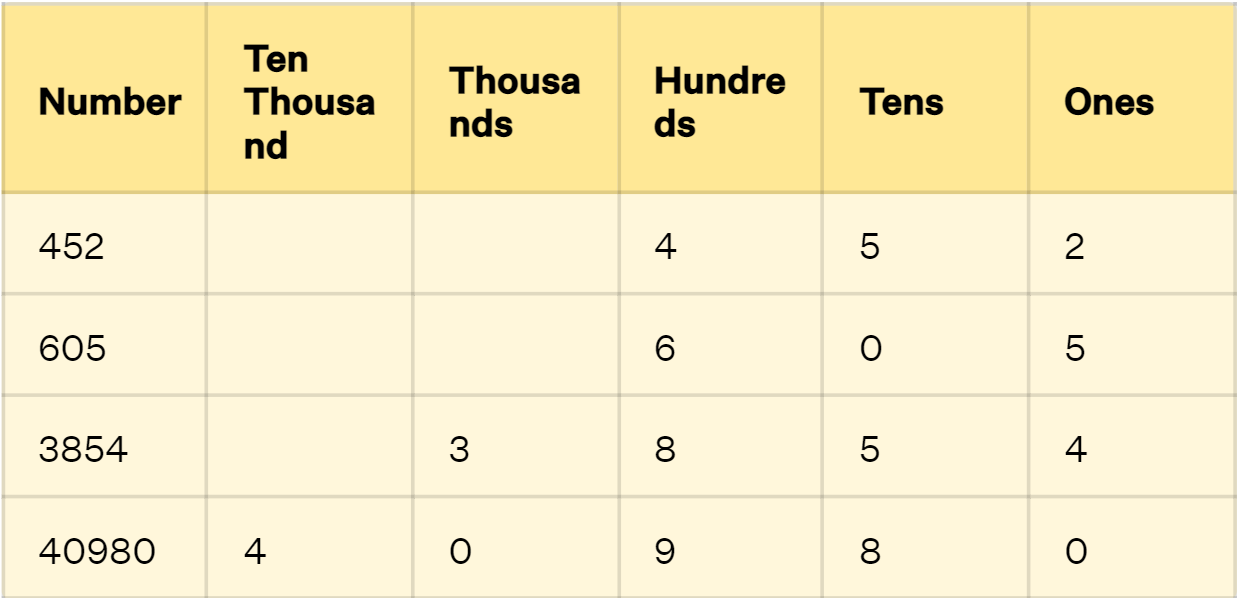
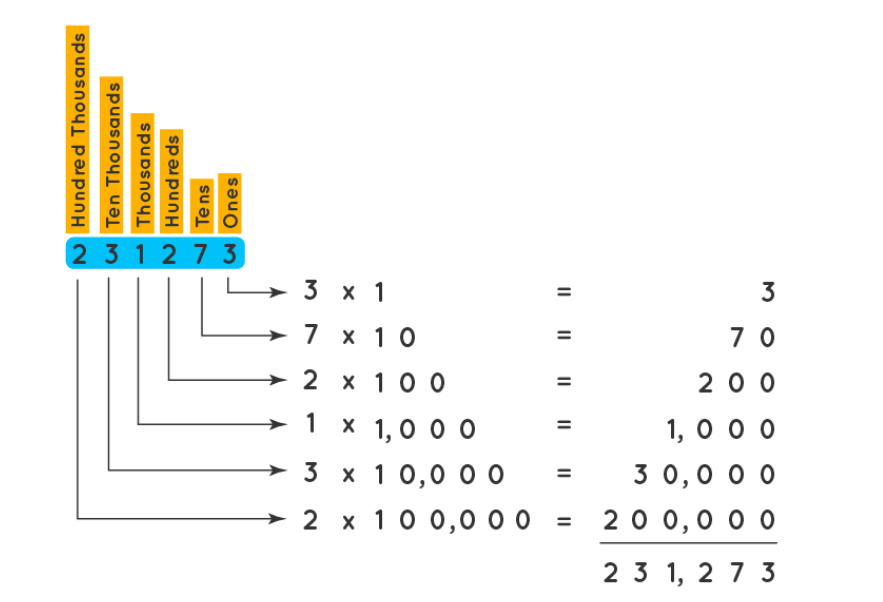
The expansion of a number is the separation of numbers based on place values. This is the intermediate step that helps us understand how the number has to be read. The expanded form helps us to know the place value of each digit within a number. Further, there are three different ways to write numbers in expanded form. The number $4537$ can be written in one way of expanded form as $4531=4000+500+30+7$, in the second way as $4531=4\times 1000+5\times 100+3\times 10+7\times 1$, and in the third way as $4537=4\times \text{thousands}+5\times \text{hundreds}+3\times \text{tens}+7\times \text{ones}$.
Expanded Form in Maths: Here are the below steps, which you can follow to write the expanded form:

$\text{(i) Reversing the digits – two digit number}$
Baccho, iss section ko hume ek game se start krenge! Follow the given steps and observe:

Baccho, iss section m hum kuch puzzles dekhenge jinme ek digit ki jagah ek letter hoga in an arithmetic sum and we'll have to find out which digit does that letter represent in a way that it satisfies the sum. We'll deal with problems of addition and multiplication.
Here are two rules we follow while doing such puzzles.
$1.$ Each letter in the puzzle must stand for just one digit. Each digit must be represented by just one letter.
$2.$ The first digit of a number cannot be zero. Thus, we write the number “sixty three” as $63$, and not as $063$, or $0063$.
A rule that we would like to follow is that the puzzle must have just one answer.
Example 1: Find the values of the letters in the following.

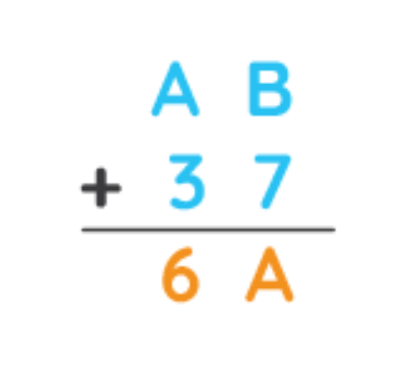
Solution:
Each letter in the given puzzle must stand for just one digit.
The operation performed here is addition.
The addition of $A$ and $3$ is giving $6$. There can be two cases.
$\left(a\right)$ First step is not producing a carry. In that case, $A$ turns out to be $3$ as $3+3=6$. Considering the first step in which the addition of $B$ and $7$ is giving $A$ (i.e., $3$), $B$ should be a number such that the unit’s digit of this addition comes to be $3$. It is possible only when $B=6$.
In this case, $B=6+7=13$.
However, $A$ is a single-digit number. Hence, it is not possible.
$\left(b\right)$First step is producing a carry. In that case, $A$ turns out to be $2$ as $1+2+3=6$.
Considering the first step in which the addition of $B$ and $7$ is giving $A$ (i.e., $2$), $B$ should be a number such that the unit’s digit of this addition comes to be $2$. It is possible only when $B=5$ and $5+7=12$.

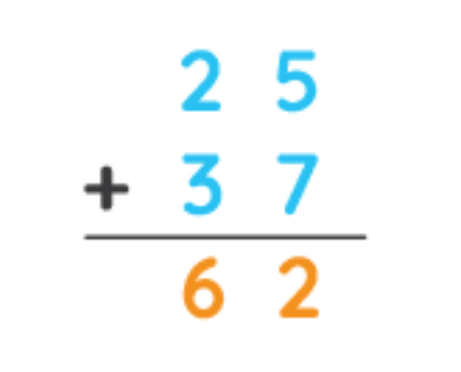
Hence, the values of $A$ and $B$ are $2$ and $5$ respectively.
Example 2: Find the values of the letters in the following and give reasons for the steps involved.

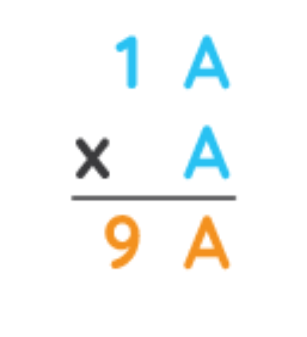
Solution:
Each letter in the given puzzle must stand for just one digit.
The operation performed here is multiplication.
The multiplication of $A$ and $A$ gives a number whose one’s digit is $A$ again.
Hence, $A$ must be $1$ or $6$.
Let $A$ be $1$. Therefore, $A\times A=1\times 1=1\ne 9$. So, the value of $A$ cannot be $1$.
Hence, $A$ must be $6$ only. For $A=6$, we get $A\times A=6\times 6=36$ and $3$ will be a carry for the next step.
Therefore, $A\times 1=6\times 1+3$(Carried on) $=9$

Hence, the value of $A=6.$
Look at more examples to understand better.

Find $Q$ in the addition. $31Q+1Q3=501$

Here, $31Q+1Q3=501$
If we add unit digits $Q$ and $3$, it becomes $Q+3$.
So, $Q+3$ should be equal to the unit digit of $501$ that is $1$.
So, $Q$ can be $8$. If we replace $Q$ by $8$ and verify the addition, it satisfies the addition. So,
$Q=8$

Find the values of the letters and give reasons for the steps involved. $2AB+AB1=B18$

$2AB+AB1=B18$
If we look at the unit digits of the given equation,
only value possible for $B$ is $7$ as $7$+$1$ = $8$.
So,
$2A7+A71=718$
Now, only possible value for $A$ can be $4$ as $4$+$7$ =$11$.
If we try $A=4$ and $B=7$, then, it satisfies our addition. So, this is the correct answer.

Find the values of the letters and give reasons for the steps involved. $3A+25=B2$

$3A+25=B2$
If we add only unit digits, then,
$A+5=2$
Only possible value for $A$ is $7$.
So, addition is $37+25=62$.
So, $B=2$.

Baccho, aapne apni previous classes m $10,5,2,3,6,4,8,9,11$ k divisibility tests k baare m pdha hua hai. Iss section m hum pdhenge ki why do these divisibility tests work.
$\text{1.Divisibility by 10}$
Baccho $10$ ka divisibility test sabse easy hota hai smjhne k lie. Let's start by observing multiples of $10$: $10,20,30,40,50...$ and so on.
Jaisa ki aap dekh skte hai $10$ k saare multiples $0$ p end hote hai. Which implies that if a number has $0$ at its ones place then it is divisible by $10$.
We only need to remember the rules of place value. Take the number. $...cba$; this is a short form for:
$...+100c+10b+a$
Here $a$ is the one’s digit, $b$ is the ten’s digit, $c$ is the hundred’s digit, and so on. The dots are there to say that there may be more digits to the left of $c$.
Since $10,100,...$ are divisible by $10$, so are $10b,100c,...$ . And as for the number $a$is concerned, it must be a divisible by $10$ if the given number is divisible by $10$. This is possible only when $a=0$.
Hence, a number is divisible by $10$ when its one’s digit is $0$.
$\text{2. Divisibility by 5}$
Look at the multiples of $5$:
$5,10,15,20,25,30,35,40,45,50$
We see that the one’s digits are alternately $5$ and $0$, and no other digit ever appears in this list.
So, we get our test of divisibility by $5$.
If the ones digit of a number is $0$ or $5$, then it is divisible by $5$.
Let us explain this rule. Any number $...cba$ can be written as:
$...+100c+10b+a$
Since $10,100$ are divisible by $10$ so are $10b,100c,...$ which in turn, are divisible by $5$ because $10=2\times 5$. As far as number $a$ is concerned it must be divisible by $5$ if the number is divisible by $5$. So $a$ has to be either $0$ or $5$.
$\text{3. Divisibility by 2}$
Baccho, humne pdha hai ki $2$ ki divisibility test k lie hum dekhte hai ki agar ek number k ones place p even digits (0,2,4,6,8) hai ya nahi. If they are even then the whole number is divisible by $2$.
The explanation for this is as follows:
Any number cba can be written as $100c+10b+a$ First two terms namely $100c,10b$ are divisible by $2$ because $100$ and $10$ are divisible by $2$. So far as $a$ is concerned, it must be divisible by $2$ if the given number is divisible by $2$. This is possible only when $a=0,2,4,6\text{or}8.$
$\text{4.Divisibility by 9 and 3}$
The divisibility rule of $3$ and the divisibility rule of $9$ are slightly similar.
$\left(i\right)$ A number $N$ is divisible by $9$ if the sum of its digits is divisible by $9$. Otherwise it is not divisible by $9$.
$\left(ii\right)$ A number $N$ is divisible by $3$ if the sum of its digits is divisible by $3$. Otherwise it is not divisible by $3$.
If the number is $‘cba’$, then, $100c+10b+a=99c+9b+(a+b+c)=9(11c+b)+(a+b+c)\{where,$9(11c+b)$is÷isib\le by\perp h$3$\text{and}$9$\}<br>Hence,÷isibilityby$9$(\text{or}$3$)ispossib\le if$a + b + c$is÷isib\le by$9$(\text{or}$3).

Check the divisibility of $21436587$ by $9$.

The sum of the digits of $21436587$ is $2+1+4+3+6+5+8+7=36$. This number is divisible by $9$ (for $36÷9=4)$. We conclude that $21436587$ is divisible by $9$.

Check the divisibility of $152875$ by $9$.

The sum of the digits of $152875$ is $1+5+2+8+7+5=28$. This number is not divisible by $9$. We conclude that $152875$ is not divisible by $9$.

If the three digit number $24x$ is divisible by $9$, what is the value of $x$?

We know that sum of numbers should be multiple of $9$
$2+4+x=9$
$6+x=9$
$x=3.$

Check the divisibility of $2146587$ by $3$.

The sum of the digits of $2146587$ is $2+1+4+6+5+8+7=33$. This number is divisible by $3(f\text{or}33÷3=11)$. We conclude that $2146587$ is divisible by $3$.

$1.$ Numbers can be written in general form. Thus, a two digit number $ab$ will be written as $ab=10a+b$.
$2.$ The general form of numbers are helpful in solving puzzles or number games.
$3.$ The reasons for the divisibility of numbers by $10,5,2,9$ or $3$ can be given when numbers are written in general form.

$1.$ Baccho iss chapter m humne apni previous knowledge related to number system ko use krke aur topics explore kiye.
$2.$ We learnt about how to express a number in general/expanded form and how we can use the same knowledge to learn about tricks related to numbers.
$3.$ Humne ye bhi seekha ki agar hume ek given sum ya multiplication m ek digit k jagah ek alphabet given ho to hum use kaise crack krke uss alphabet ki numerical value nikaal skte hai.
$4$. Lastly, we used variables to justify various divisibility tests for numbers like $10,5,2,3,9$.