MENSURATION for Class 8 MATHS
INTRODUCTION
Baccho, mensuration mathematics ki vo branch hoti hai jo ki geometrical shapes aur unke area, surface area, volume and perimeters se deal krti hai.. Aap sabne apne previous classes m iss topic k baare m pdha hua hai aur hum jaante hai ki mensuration hume day to day activities m bohot help krta hai. For example, using mensuration, we can find the number of tiles needed to cover a particular floor, or cost of painting a particular wall or the length of cloth needed to make a particular shaped dress, etc. Iss chapter m hum aur plane figures k areas nikaalna seekhenge aur ye bhi jaanenge ki hum 3D shapes (cube, cuboid, cylinder, etc) k surface area aur volume kaise nikaal skte hai. So let's begin!
Let us Recall
Baccho, before learning about new concepts, let's recall some topics from our previous classes.
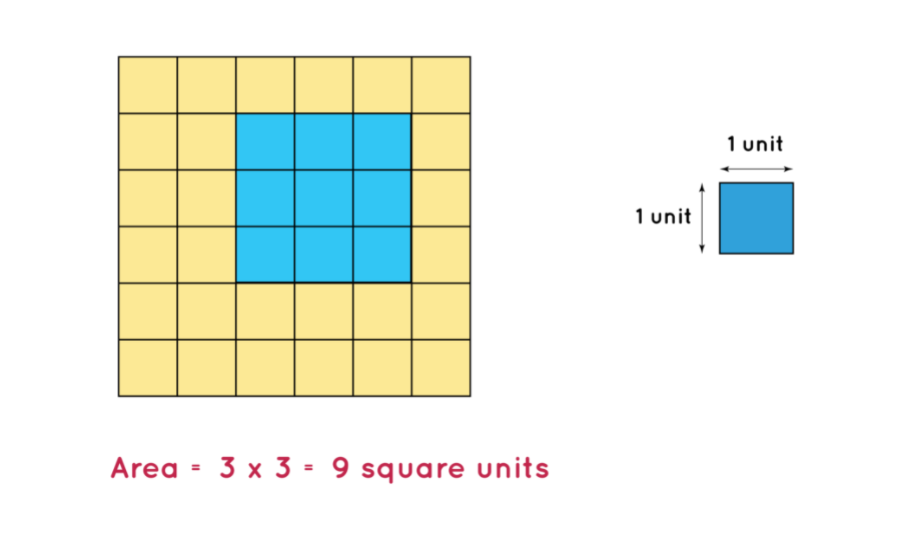
Definition of Area
Area is defined as the amount of space that is occupied by any shape, object, or flat surface. The total number of square units that can fit into a shape or an object or a flat surface defines the actual area. The concept of finding an area can easily be understood by using a square grid paper. The total number of unit square enclosed in the figure gives the area of that figure. For example, the blue square occupies 9 squares, which means the area of the square is 9 square units. In real life, we use the concept of area to find out the amount of space that is to be painted in a wall, the dimensions of a room, the space in the floor of a room that is to be covered by tiles, making a lawn at the backyard and so on.
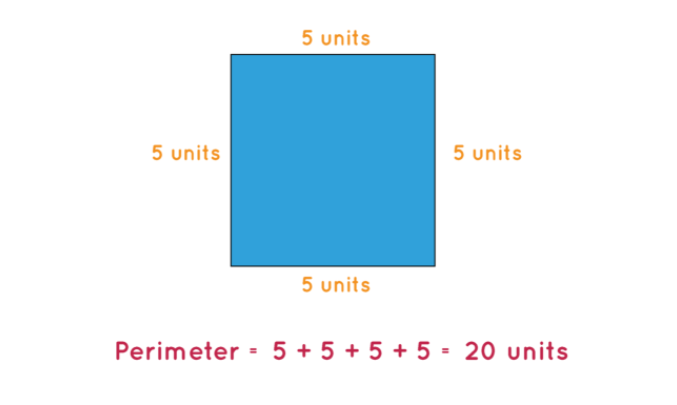
Definition of Perimeter
The word 'perimeter' is derived from the Greek word 'Perimetron'. 'Peri' means 'around' and 'Metron' means 'measure'. The perimeter of a shape is calculated by adding up the length of all the sides or by measuring the outer boundary of a shape or an object. Some real-life uses of the perimeter are to know about the size of a photo frame, length of a lawn that for which we need to put a fence. Perimeters of small objects can be found by taking a string or a thread around the object for which perimeter is to be found. In the case of polygons, their perimeter can be found by adding up the sides of the polygon and expressing them in the given units. The figure given below shows the perimeter of a square, which is 20 units.
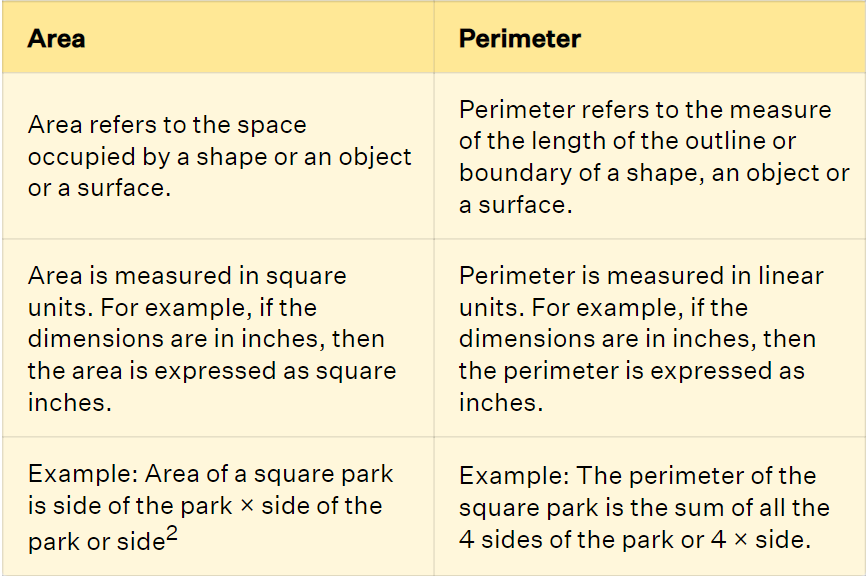
What is the Difference Between Area and Perimeter?
The following table lists the important differences between area and perimeter.
Area and Perimeter Formula
The table given below lists some important formulas for the area and perimeter of some common shapes.

Area of Trapezium
Baccho, aap sabne quadrilterals k baare apni previous classes m pdha hai. Aap sab jaante hai ki square aur rectangle k areas kaise nikaale jaate hai. Iss section m hum ek special quadrilateral k area k baare m pdhenge jise kehte hai trapezium. The area of a trapezium is defined as the number of unit squares that can fit into it and it is measured in square units (like cm2,m2,∈2, etc). A trapezium is a type of quadrilateral that has one pair of parallel sides(generally referred to as bases). The other pair of sides of a trapezium can be non-parallel and are known as legs. The area of a trapezium is the total space covered by a trapezium in a two-dimensional plane. For example, if 20 unit squares each of length 1 ∈ can be fit inside a trapezium, then its area is 20∈2. It is not always possible to draw unit squares and hence measure the area of a trapezium. We will learn about the area of a trapezium and the formula to calculate it on this page.
Area of Trapezium Formula
The area of a trapezium can be calculated using the lengths of two of its parallel sides and the distance (height) between them. The formula to calculate the area (A) of a trapezium using base and height is given as,
A=12(a+b)h where,
a and b= bases of trapezium, and,
h= height (the perpendicular distance between a and b)

Area of a General Quadrilateral
Baccho, for special quadrilaterals, we have formulas to calculate their area but there's a method which can be used to find the area of quadrilaterals in general. Iss method ko kehte hai "Triangulation". Iss method m basically hum ek quadrilateral ko triangles m breakdown krte hai aur triangle k area k formula se we get to calculate the area of the quadrilateral.
If the quadrilateral does not belong to one of the types that are mentioned above, then we can find its area either by dividing it into two triangles. Consider a quadrilateral ABCD in which the length of the diagonal BD is known to be d. ABCD can be divided into two triangles by the diagonal BD. To find its area, we should be knowing the heights of the triangles ABD and BCD. Let us assume that the heights of the triangles BCD and ABD are given to be h1 and h2 respectively. We will find the area of the quadrilateral ABCD by adding the areas of the triangles BCD and ABD.
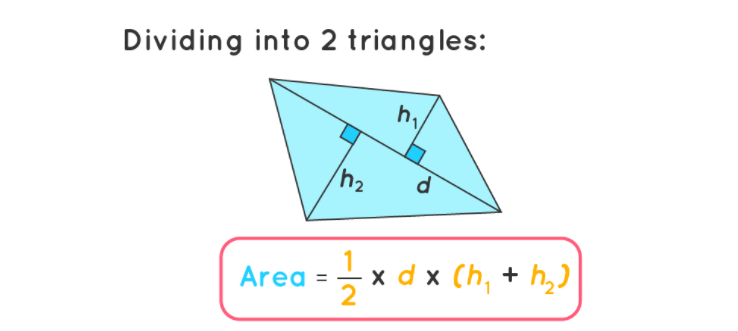
Here, the area of the triangle BCD=(12)×d×h1.
The area of the triangle ABD=(12)×d×h2.
From the above figure, the area of the quadrilateral ABCD= "area of" △BCD+area of△ABD.
Thus, the area of the quadrilateral ABCD=(12)×d×h1+(12)×d×h2
=(12)×d×(h1+h2).
Thus, the formula used to find the area of a quadrilateral when one of its diagonals and the heights of the triangles (formed by the given diagonal) are given is,
Area=(12)×Diagonal×(Sum of heights)
Area of special quadrilaterals
Baccho, for special quadrilaterals, we have formulas to calculate their area but there's a method which can be used to find the area of quadrilaterals in general. Iss method ko kehte hai "Triangulation". Iss method m basically hum ek quadrilateral ko triangles m breakdown krte hai aur triangle k area k formula se we get to calculate the area of the quadrilateral.
If the quadrilateral does not belong to one of the types that are mentioned above, then we can find its area either by dividing it into two triangles. Consider a quadrilateral ABCD in which the length of the diagonal BD is known to be d. ABCD can be divided into two triangles by the diagonal BD. To find its area, we should be knowing the heights of the triangles ABD and BCD. Let us assume that the heights of the triangles BCD and ABD are given to be h1 and h2 respectively. We will find the area of the quadrilateral ABCD by adding the areas of the triangles BCD and ABD.
IMAGE 6
Here, the area of the triangle BCD=(12)×d×h1.
The area of the triangle ABD=(12)×d×h2.
From the above figure, the area of the quadrilateral ABCD= "area of" △BCD+area of△ABD.
Thus, the area of the quadrilateral ABCD=(12)×d×h1+(12)×d×h2
=(12)×d×(h1+h2).
Thus, the formula used to find the area of a quadrilateral when one of its diagonals and the heights of the triangles (formed by the given diagonal) are given is,
Area=(12)×Diagonal×(Sum of heights)
Area Formulas of Different Types of Quadrilaterals
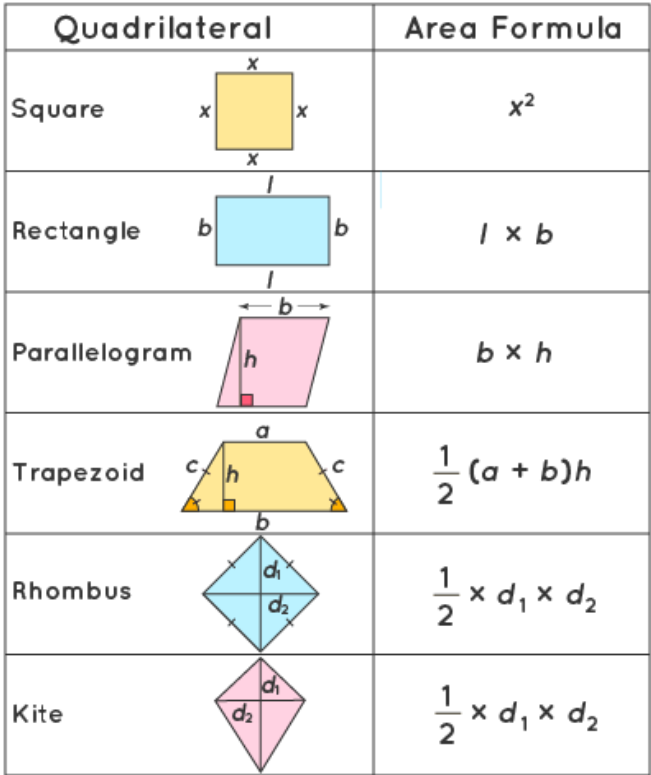
Example 1
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45cm and 30cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs.4.
Area of a rhombus=12×D1XXD2 Where D1 and D2 are diagnols of rhombus.
substituting values we get=>12×45×30=675(cm)2
area of 3000 such tiles=3000×675=2025000(cm)2=202.5(m)2
cost of polishing=202.5×4=Rs.810
Area of a Polygon
Baccho, humne jo triangulation ka concept seekha, hum use expand krke baaki polygons bhi apply kr skte hai. Hum complex polygons ko lekr unhe triangles k form m divide kr skte hai to calculate area. Look at the following diagram to understand how:

Example 2
The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1m and 1.2m and perpendicular distance between them is 0.8m.
Area=1/2* Sum of parallel sides*perpendicular distance
Area=1/2(1+1.2)(0.8)
Area=0.88m2.
Example 3
The area of a trapezium is 34cm2 and the length of one of the parallel sides is 10cm and its height is 4cm. Find the length of the other parallel side.
Area of a trapezium, A = 1/2**(Sum of parallel sides)**distance between parallel sides
One of parallel side =10 cm
Let other parallel side =x cm
Distance between parallel sides =4 cm
So,
34=12∗(10+x)∗4
684=10+x⇒x=17−10=7
So, length of other paralel side is 7cm.
Example 4
The area of a rhombus is 240cm2 and one of the diagonals is 16cm. Find the other diagonal.
area=1/2*multiplication of diagnols
240=1/2*x*16
x=30cm.
Example 5
There is a regular hexagon MNOPQR of side 5cm . aman and ridhima divided it into two different ways . Find the area of this hexagon both ways.
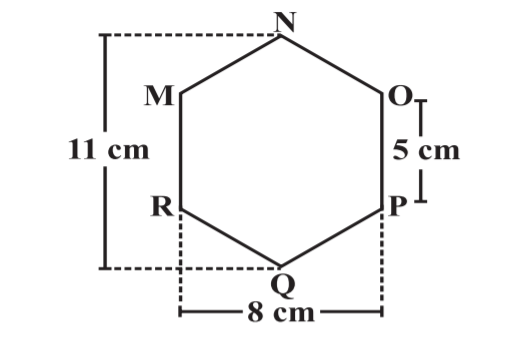
for ridhima
total area = area 1 + area 2 + area 3
=2×area1 + area 2
=2×12×8×3+8×5
=24+40=64cm2
for aman
total area = area of 1 + area of 2
= area of 1
=2×12×(5+11)×4
=64cm2
Solid Shapes
Solid shapes are nothing but solids that consist of 3 dimensions, namely length, breadth, and height. Solid shapes are also known as 3D shapes. These solid shapes occupy space and are found in our day-to-day life. We touch, feel, and use them.
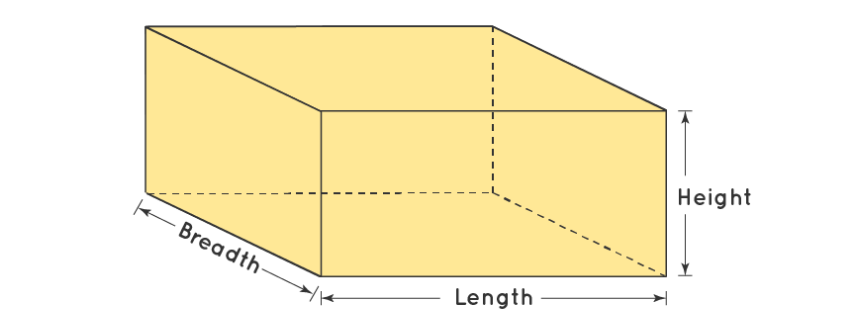
1.Cuboid
A cuboid is a three-dimensional solid shape that has 6 faces, 8 vertices, and 12 edges. It is one of the most commonly seen shapes around us which has three dimensions: length, width, and height. Sometimes a cuboid is confused with a cube since it shares some properties of a cube, however, they are different from each other.
2.Cube
A cube is a three-dimensional object that has 6 congruent square faces. Dimensions of all the 6 square faces of the cube are the same. A cube is sometimes also referred to as a regular hexahedron or as a square prism. It is one of the 5 platonic solids. Some real-life examples of a cube are an ice cube, a Rubik's cube, a regular dice, etc.
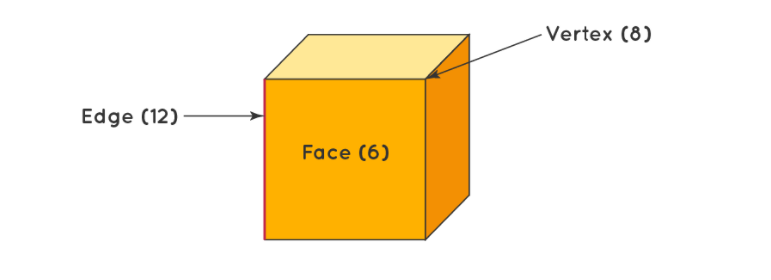
The properties are:
3.Cylinder
A cylinder is a 3D solid shape that consists of two identical and parallel bases linked by a curved surface. These bases are like circular disks. The line passing from the center or joining the centers of two circular bases is called the axis of the cylinder shape. The distance between the two bases is called perpendicular distance and is represented as height, “h”. The two circular bases have a distance from the center to the outer boundary which is known as the radius of the cylinder, represented by “r”. The cylinder is a combination of 2 circles +1 rectangle. Look at the given image showing the formation of the cylinder shape.
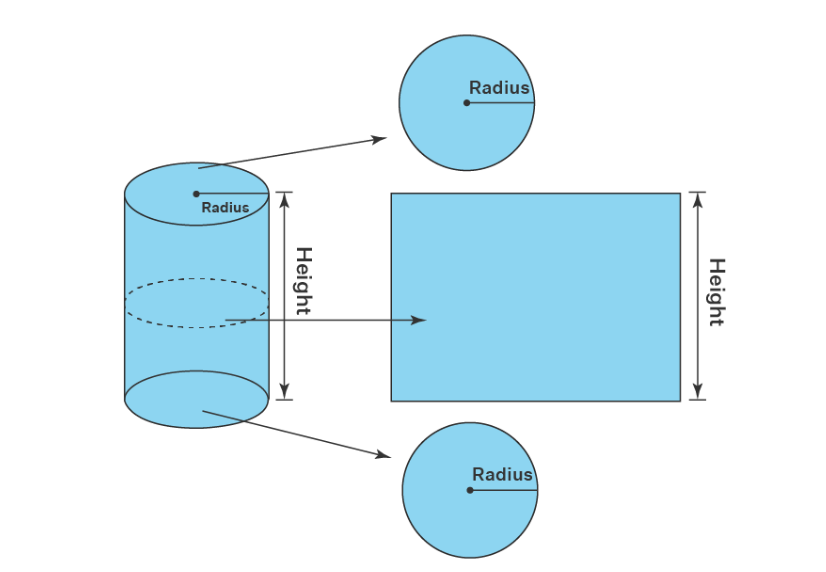
Surface Area of Cube, Cuboid and Cylinder
Baccho, surface area ka mtlb hota hai kisi shape k faces ka area. There are two types of surface areas: Total surface area (TSA) and Lateral surface area (LSA).
Baccho, jab hum ek shape ko cut open krte hai to hume uske saare faces alag alag mil jaate hai. Inn saare faces k areas ko milakr hume uss solid shape ka total surface area milta hai. Jab hum iss Total Surface Area m se top and bottom faces ka area subtract krdete hai to hume miljaata hai Lateral Surface Area (LSA) ya Curved Surface Area(CSA).
1.Surface Area of Cuboid
The surface area of the cuboid is the total area of all its surfaces. As a cuboid is a three-dimensional (dimensions being length, breadth, and height) solid shape, the value of its surface area will depend on the dimensions of length, breadth, and height. The change in any of the dimensions of a cuboid changes the value of the surface area of a cuboid. The unit of the surface area of a cuboid is given as the (unit)^2.
A cuboid can have two kinds of surface areas:
The total surface area of the cuboid is obtained by adding the area of each face while the lateral surface area of the cuboid is found by finding the area of each face excluding the base and the top. The total surface area is denoted by "TSA" while the lateral surface area is denoted by "LSA". The total surface area and lateral surface area can be expressed in terms of length (l), breadth(b), and height of cuboid(h) as:
Total Surface Area of Cuboid, TSA = 2 (lb + bh + lh)
Lateral Surface Area of Cuboid, LSA = 2h (l + b)
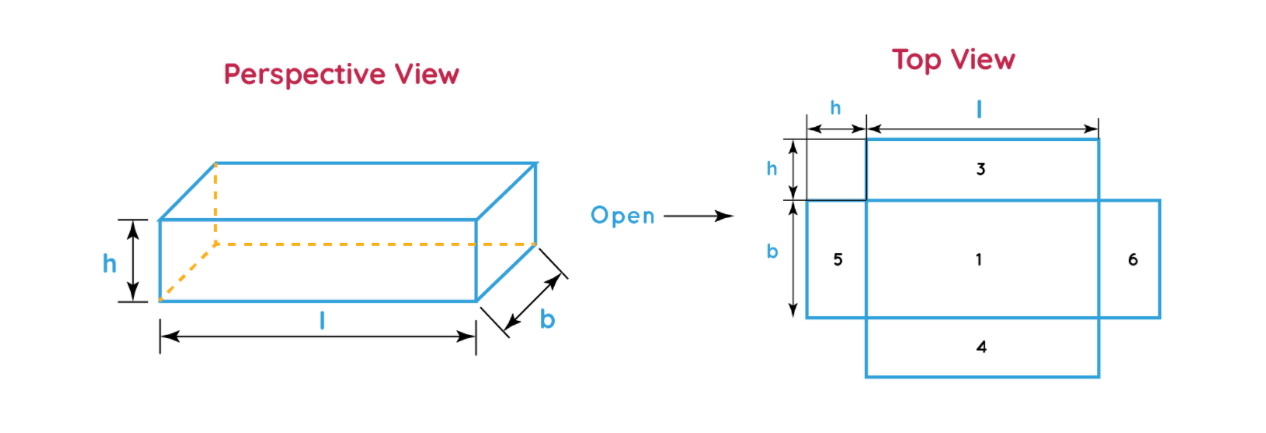

Hence, the total surface area of six faces =(l×b)+(l×b)+(l×h)+(l×h)+(b×h)+(b×h).
Clearly, total surface area, TSA=(2×l×b)+(2×b×h)+(2×l×h)
Thus, the surface area TSA of any cuboid of dimensions l,b, and h will be TSA=2(lb+bh+lh)
The lateral surface area of a cuboid is the combined surface area of the four vertical faces. In the diagram above, the two horizontal faces (that is, face 1 and face 2) will be removed from the total surface area and only the vertical faces remain. The lateral surface area of cuboid will be, LSA=2(lb+bh+lh)−(2×l×b)=(2×l×h)+(2×b×h)=2h(l+b).
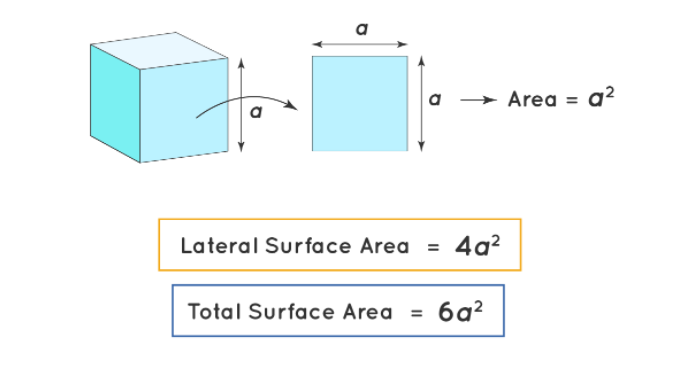
2.Surface Area of a Cube
There are two types of surface areas of a cube - Lateral surface area and Total surface area
Lateral Surface Area of a Cube
The lateral area of a cube is the sum of areas of all side faces of the cube. There are 4 side faces so the sum of areas of all 4 side faces of a cube is its lateral area. The lateral area of a cube is also known as its lateral surface area (LSA), and it is measured in square units.
LSA of a Cube =4a2
where a is the side length.
Total Surface Area of a Cube
The total surface area of the cube will be the sum of the area of the base and the area of vertical surfaces of the cube. Since all the faces of the cube are made up of squares of the same dimensions then the total surface area of the cube will be the surface area of one face added five times to itself. It is measured as the "number of square units" (square centimeters, square inches, square feet, etc.). Therefore, the formula to find the surface area of a cube is:
Total Surface Area (TSA) of a Cube =6a2
where a is the side length.
3.Surface Area of a Cylinder
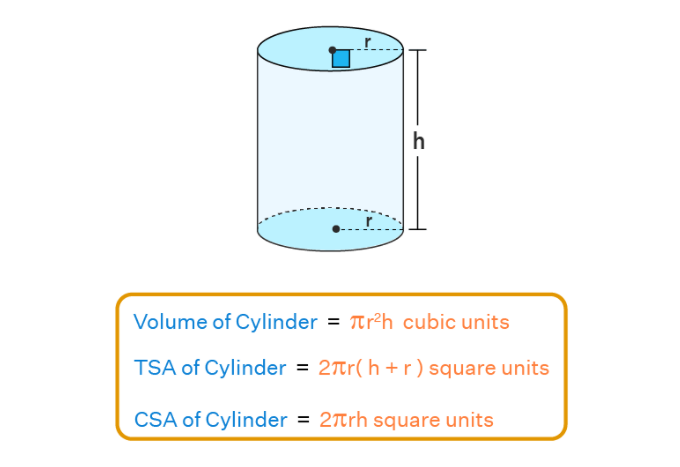
Curved Surface Area of Cylinder
The curved surface area is also termed lateral surface area. The area formed by the curved surface of the cylinder i.e. space occupied between the two parallel circular bases is known as its CSA. The formula for cylinder curved surface area is given as,
Curved Surface Area (CSA) =2πrh square units
(Note: ‘h’ is the height, ‘r’ is the radius, and the value of π is 227 or 3.14 approximately).
Total Surface Area of Cylinder
The total surface area defines the total area that it occupies including the bases. The cylinder consists of two circles and one curved sheet. So, in order to find out the total surface area of a cylinder, we calculate the curved surface area and the area of two circles.
Curved Surface Area (CSA) = Circumference × Height
CSA=2πr×h
Area of a Circle = πr2
Total Surface Area (TSA)= Curved Surface Area + 2(Area of a circle)
Total Surface Area (TSA)=2πrh+2πr2=2πr(h+r) square units
(Note- ‘h’ is the height and ‘r’ is the radius. There are two circles, so we multiply the area of the base circle by 2)
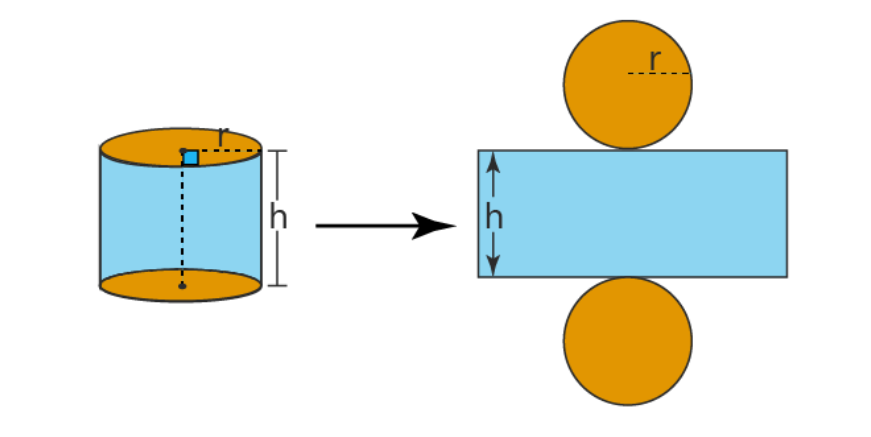
Example 6
An aquarium is in the form of a cuboid whose external measures are 80cm×30cm×40cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed?
Required Area will be A = Area of base + Area of both side faces + Area of back face
A=lb+2bh+hl
where l is length, b is breadth and h is height.
Here, l=80cm,b=30cm,h=40cm
So, A=(80∗30+2∗30∗40+80∗40)cm2
A=2400+2400+3200=8000cm2
Example 7
The internal measures of a cuboidal room are 12m×8m×4m . Find the total cost of whitewashing all four walls of a room, if the cost of white washing is Rs 5 per m2. What will be the cost of white washing if the ceiling of the room is also whitewashed.
total area to be white washed= area of 1+ 2+3 +4
= 2(area of (1) + (2))
= 2⋅(4×8+12×4)
= 2×(32+48)
= 160m2
cost of painting = 5×160
=800rs
Area = 160m2+area of ceiling
=160+12×8
=256m2
total cost = 256×5=1280 rs
Example 8
Find the height of a cylinder whose radius is 7cm and the total surface area is 968cm2.
The total surface area of a cylinder A=2πr(r+h)
Here, A=968cm2,r=7cm
So,
968=2∗227∗7(7+h)
96844=7+h⇒h=22−7=15cm
Volume of Cube, Cuboid and Cylinder
Baccho, volume ka mtlb hota hai koi solid shape kitna space occupy krti hai. For example, aapki almirah ka volume aapke room k volume se kam hota hai kyunki aapka room zyada space occupy krrha hota hai. Humne abhi three basic solid shapes k surface areas k baare m pdha, ab hum unhi shapes k volumes k baare m study krenge. Baccho, hum volumes apni daily life m bohot jagah use krte hai, for example, while filling a cylinderical container with milk, or keeping cuboidal books insider a cuboidal box, etc. So let's study how to calculate these volumes.
1.Volume of Cuboid
The volume of the cuboid is the measure of the space occupied within a cuboid. The cuboid is a three-dimensional shape that has length, breadth, and height. If we have a rectangular sheet and we go on stacking such sheets, we will end up getting a shape that has some length, breadth, and height. This stack of sheets looks like a shape that has 6 faces, 12 edges, and 8 vertices hence giving us the shape of a cuboid. The unit of volume of cuboid is given as the (unit)3
The volume of the cuboid depends on the length, breadth, and height of the cuboid, hence changing any one of those quantities changes the volume of the shape.
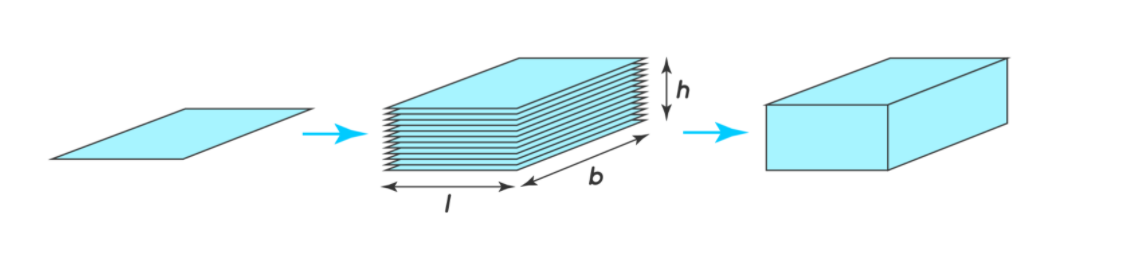
Formula
The formula for the volume of the cuboid can be derived from the concept explained on rectangular sheets. Let the area of a rectangular sheet of paper be 'A', the height up to which they are stacked be 'h' and the volume of the cuboid be 'V'. Then, the volume of the cuboid is given by multiplying the base area and height.
The volume of cuboid = Base area xx Height
The base area for cuboid =l×b
Hence, the volume of a cuboid, V=l×b×h=lbh
2. Volume of a Cube
The volume of a cube is the space occupied by the cube. The volume of a cube can be found out by finding the cube of the side length of the cube. To determine the volume of a cube, there are different formulas based on different parameters. It can be calculated using the side length or the measure of the cube's diagonal and it is expressed in cubic units of length. Hence, the two different formulas to find the volume of the cube are:
The Volume of a Cube =a3
where a is the length of the side of a cube.
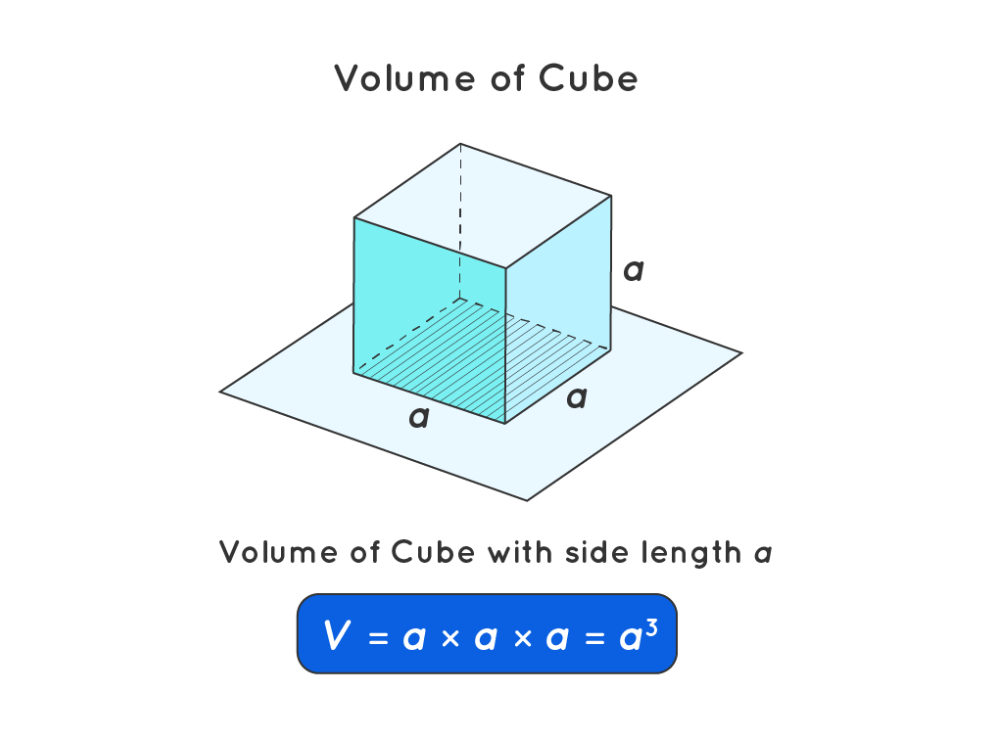
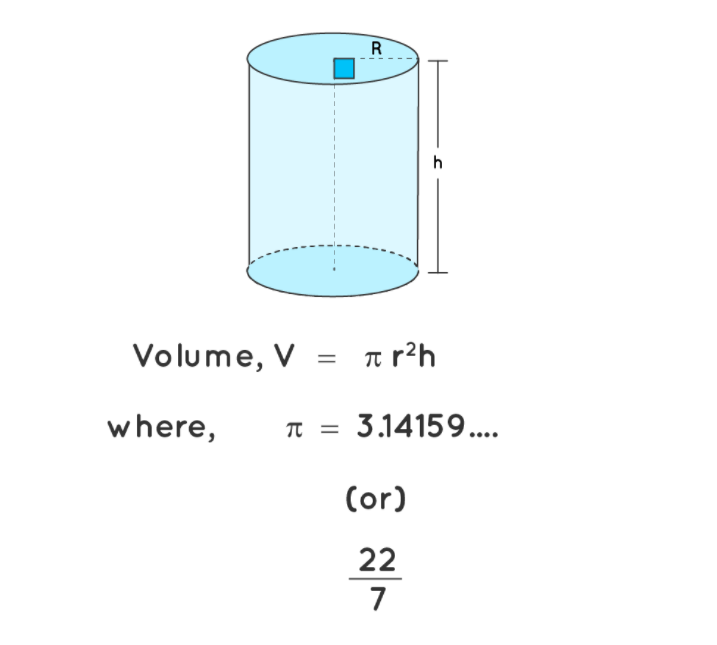
3.Volume of Cylinder
The cylinder volume defines the density or amount of space it occupies. If we want a cylinder to fill with water, then the amount of water needed can be calculated by finding its volume.
The volume of a cylinder = Area of a circle × height
Volume=πr2×h
The volume of a cylinder, V=πr2h cubic units
where ‘h’ is the height and ‘r’ is the radius.
Volume and Capacity
Baccho, volume aur capacity inter-related terms hote hai.
If a water tin holds 100cm3 of water then the capacity of the water tin is 100cm3.
Capacity is also measured in terms of litres. The relation between litre and cm3 is, 1mL=1cm3,1L=1000cm3. Thus, 1m3=1000000cm3=1000L.
Example 9
A godown is in the form of a cuboid of measures 60m×40m×30m. How many cuboidal boxes can be stored in it if the volume of one box is 08m3 ?
volume of godown = 60×40×30
=72000m3
no of boxes = 720000.8
=90,000 boxes
Example 10
A rectangular paper of width 14cm is rolled along its width and a cylinder of radius 20cm is formed. Find the volume of the cylinder ? (Take 227 for π )
volume =πr2a
=227⋅20⋅20⋅14
=22⋅800
=17600cm3
SUMMARY
1. Area of
(i) a trapezium = half of the sum of the lengths of parallel sides × perpendicular distance between them.
(ii) a rhombus = half the product of its diagonals.
2. Surface area of a solid is the sum of the areas of its faces.
3. Surface area of:
a cuboid =2(lb+bh+hl)
a cube =6l2
a cylinder =2πr(r+h)
4. Amount of region occupied by a solid is called its volume.
5. Volume of:
a cuboid =l×b×h
a cube =l3
a cylinder =πr2h
6. (i) 1cm3=1mL
(ii)1L=1000cm3
(iii)1m3=1000000cm3=1000L
Let's Revise
1. Baccho, iss chapter m humne plane figures k areas and solid shapes k surface areas and volume k baare m pdha.
2. Area basically vo region hota hai jo ek shape ek plane p occupy krti hai. Humne previous classes m basic shapes k areas k baare m pdha hua tha like square and rectangle. Iss chapter m humne trapezium, rhombus, polygons jaisi shapes ko explore kia.
3. Surface area do types k hote hai: Total surface area and Curved/Lateral Surface Area.
4. Total surface area basically ek solid shape ki saare faces k area ko milkar bnta hai.
5.Jab hum total surface area m se top and bottom faces k areas ko subtract kr dete hai to humne Curved surface area milta hai.
6. Volume se hume ye pta chlta hai ki ek solid shape kitna space occupy krti hai.
7. We learnt how to calculate the volumes of cuboid, cube and cylinder.
8. Capacity ka mtlb hota hai ki solid shape kitni quantity hold kr skti hai.