LINEAR EQUATIONS IN ONE VARIABLE for Class 8 MATHS
INTRODUCTION
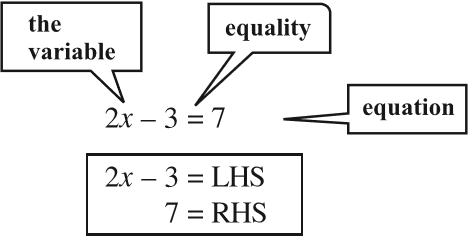
Bachcho apne pichli classes mein algebraic expressions aur equations ko dekha hoga. Let's recall it. Aisi expressions jinme variables, constants aur operations jaise addition, multiplication, etc involved ho unhey hum algebraic expressions kahte hai. Agar 2 expressions ek dusre ke equal ho to ussey equations kahte hai (in short equality is missing in algebraic expressions). Wait, now the question arises what is variables and coefficients ? Variables wo number hote hai jinki value hume pta nhi hoti aur ihne x,y, etc. se denote kiya jaata hai jabki coefficient wo number kahlate hai jo variable ko follow karte hai i.e., jo number variables se multiplied hote hai.
7x+3,y+y2,2xy+5 are the examples of expressions. 6x=35,2x–4=1,6z−10=2 are the examples of equations. Aap dekh sakte ho ki aise bhi expressions hai jisme ek se jyada variables hai lekin es chapter mein hum sirf ek variable wale expressions se equations form karenge i.e., es chapter mein hum linear expressions in one variables se deal karenge. Ab ye linear expressions kya hoti hai ? Aise expressions jisme variable (variable of one type that means the expressions contains only x or y, etc.) ki highest power one ho ussey linear expressions in one variable kahte hai aur inse form hone wali equations linear equations in one variable kahalti hai. Aap soch rhey honge ki hume variables aur equations ko jaan liya magar variables ki kuch values bhi to hoti hongi jiski wajh se equation mein LHS=RHS hoga i.e. equation ko satisfy karega. Variables ki values jo equation ko satisfy karti hai unhey hi solutions kahte hai.
Isse hum kuch es tarh se find karte hai,
Hum aisa assume karte hai ki equation ki dono side balanced hai. Hum equation ki dono side same mathematical operations perform karte hai jisse balancing disturb na ho aur aise hi kuch steps se hume solutions mil jata hai.
Linear equation in one variable
A linear equation in one variable is an equation that can be written in the form
ax+b=0, where a and b are real numbers and a≠0.
Linear equations in one variable ko first-degree equations kahte hai kyonki es type ki equations mein variable ki highest power (degree) one hoti hai. Bachcho power kise kahte hai ye to aap jante hi ho jaise agar x2 likha hai to yha x ki power 2 hai and so on. 2x+10=7 is an algebraic equation in which LHS is 2x+10 and RHS is 7.
Solution : A solution is the true value of the variables in the algebraic equations for which the equation holds true and LHS=RHS.
Bachcho aasan bhasha mein solution of linear equation wo real values kahlati hai jinhe equation mein variables ki jagh rakhne se equation satisfy kare [LHS=RHS].
For the above equation,
2×(−32)+10=7=RHS. Hence x=−32 is the solution.
The graph of the linear equation is represented by a straight line as the equation has solution in the form of real numbers which can be easily plotted in a graph.
Note : The coefficient (jo real value equation mein variable ke sath multiplied hota hai) of a variable in an equation and the solution of that equation need not be an integer i.e. iska mtlb ye hai ki coefficient aur variable jaruri nhi hai ki integer hi ho as you can see in example above where we got −32 which is a rational no. as the solution.
Solving Equations which have Linear Expressions on one Side and Numbers on the other Side
Bachcho algebraic methods ko solve karne ke lie bahut se methods hote hai jaise :
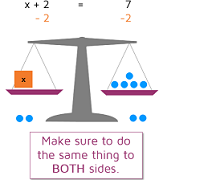
(i) Balancing method
Es
method mein hum balancing ko disturb na karte hue equation ki dono sides mein same number ko add, subtract, multiply ya divide karte hai. Chalo isse example se samjhte hai.
Example : Find the solution of 7x−11=24.
Solution :
Step 1. Hum given equation mein dono side 11 ko plus karenge.
7x−11+11=24+11
⇒7x+0=35⇒7x=35
Step 2. Hum dekh sakte hai ki variable x ke saath 7 multiplied hai islie ab hum equation ki dono sides ko 7 se divide karenge.
7x7=357
⇒x=5
Hence x=5 is the solution of the equation.
Hum isse verify bhi kar sakte hai, let's see.
LHS=7(5)−11=35−11=24=RHS.
(ii) Transposing Method
Es method mein hum variables ya constants ko equation ki ek side se dusri side transpose ya transfer karte hai jab tak solution na mil jaye lekin transfer karte waqt apko yah dhyan rakhna hai ki jab hum kisi variable ya constant ko transfer karte hai to sign change ho jata hai. The changes are as follows :
(a) + changes to −
(b)
− changes to +
(c)÷ changes to ×
(d)× changes to ÷
Chalo isse example se samjhte hai.
Example : Find the solution of 7x−11=24.
Solution :
Step 1. Hum es equation mein 11 ko LHS se RHS mein transfer karenge jisse variable es side mein ho jayega aur constants ek side.
7x=24+11=35
⇒7x=35
Step 2. Ab hum equation ko 7 se divide karenge.
7x7=357
⇒x=5
Hence x=5 is the solution of the given equation.
Example 1
Solve the equation : 17+6p=9
Transpose 17 to RHS, 6p=9−17=−8
Divide both sides of equation by 6, 6p6=−86
⇒p=−43
Hence the solution of the equation is −43.
Example 2
Solve the equation : x3+1=715
Transpose 1 to RHS, x3=715−1=−815
Multiply both sides of equation by 3, x3×3=−815×3
⇒x=−85
Hence the solution of the equation is −85.
Some Applications
Bachcho linear equation ke concept ko hum real life mein use kar sakte hai. But the question is how ? Isse hum examples se samjhenge lekin usse pahle hum kuch points dekhenge jo ki essential hai un problems ko solve karne ke lie.
Example : What number should be added to 23 to get 57 ?
Solution : From question we came to know that hume ek aisa number find karna hai jisse 23 mein add karne se 57 result milega.
Maan lo ki wo number x hai.
According to question, x+23=57
Transposing 23 to RHS, x=57−23=34
Hence the required number is 34.
Example : Sum of two numbers is 74. One of the numbers is 10 more than the other. What are the numbers ?
Solution : Bachcho hum dekh sakte hai ki hume 2 numbers find karne hai aur iske lie 2 conditions given hai.
(i) One of the numbers is 10 more than the other.
(ii) Their sum is 74.
Bachcho maan lo ki smaller number x hai, to 1st condition ke according larger number x+10 hoga.
Ab dusri condition ke according,
x+x+10=74⇒2x+10=74
Transposing 10 to the RHS,2x=74−10=64
Divide both sides by 2,2x2=642
⇒x=32
Hence smaller number is 32 and larger number be 42.
Example 3
I have a total of Rs 300 in coins of denomination Rs 1, Rs 2 and Rs 5. The number of Rs 2 coins is 3 times the number of Rs 5 coins. The total number of coins is 160. How many coins of each denomination are with me?
Let Rs 5 coins be x. So,
Rs 2 coins will be 3x, then
Rs 1 coins will be 160−x−3x.
It is given that the total amount is 300
So,
5x+6x−4x+160=300
⇒7x=140
⇒x=20
Hence Rs 5 coins are 20,
Rs 2 coins are 60 and
Rs 1 coins are 80.
Example 4
The perimeter of a rectangle is 13 cm and its width is 234cm. Find its length.
We know the perimeter(P) of a rectangle is 2(l+b),
where l is length and b is breadth or width.
Here, P=13cm
b=234cm=114cm
So, 13=2(114+l)
⇒l=132−114=154cm=334cm
Example 5
The sum of three consecutive multiples of 8 is 888. Find the multiples.
Let the first number is x.
Then, the second number = x+8
Third number = x+16
So, x+x+8+x+16=888
⇒3x=864⇒x=8643=288
So, the numbers are 288,296and304.
Solving Equations having the Variable on both Sides
Bachcho aap jante ho ki jab 2 expressions ek dusre ke equal ho tab wo equation kahlati hai. Abhi tak apne aisi equations se deal kiya hai jisme equation ki ek side variable hota tha aur dusri side mein ek numeric value jaise in equation 2x−7=4, there are two expressions, one is 2x−7 and the other is 4. But ab hum aisi equations se deal karne wale hai jisme equality (=) ke dono sides variables honge.
Let's understand it more clearly through examples.
Example : Find the solution of 2x−4=5−x.
Solution :
Step 1. Bachcho sabse pahle hume variables wali terms ko LHS mei aur numeric terms ko RHS mein lana hai.
2x−4=5−x
On transposing 4 to the right side and x to the left side, we get
⇒2x+x=5+4⇒3x=9
Step 2. Bachcho ab hume equation ki dono sides ko 3 se divide karna hai.
3x3=93
⇒x=3
Hence the solution of the given equation is x=3.
Example 6
Solve the linear equation : Solve the linear equations. x+7−8x3=176−5x2
x+7−8x3=176−5x2
⇒x+5x2−8x3=176−7
⇒6x+15x−16x6=17−426
⇒5x=−25⇒x=−5
Some More Applications
Bachcho abhi jo humne concept padha hai uske basis pe hum linear equations ki kuch aur applications ke baare mein janenge. Aur jaisa ki aap sab jante ho ki hum applications ko examples ki help se achi tarh se samjh sakte hai. So, get ready to learn about applications of linear equations.
Example : The digits of a two-digit number differ by 3. If the digits are interchanged,
and the resulting number is added to the original number, we get 143. What can be the
original number ?
Solution : Bachcho hum kisi bhi 2 digit number ko 10x+y ki form mein likh sakte hai. [y is at unit place and x is at tens digit]
Aur agar hum digits ko interchange karte hai to required 2 digit number 10y+x ki form mein likha jayega.[on interchanging y is at tens place and x is at unit place]
Maan lo ki given question ke lie 2 digit number mein unit place mein b hai aur question mein ye given hai ki tens place wali digit b se 3 differ kar rha hai. To hum maan lete hai ki tens place b+3 hai. So we can say that the two digit number is 10(b+3)+b=11b+30
Digits ko interchange karne se 2 digit number will be
10b+b+3=11b+3
Agar hum en dono numbers ka sum karte hai to result 143 ayega (as per the question).
11b+30+11b+3=22b+33=143
Or 22b=143−33=110
Or b=11022=5
Hence the unit digit will be 5 and tens digit will be b+3 which is 8. So the 2 digit number will be 85.
To check we can interchange the digits and then add to the original number and that is 85+58=143.
Note : This is the solution when we choose the tens digits to be 3 more than the unit’s digits.
What happens if we take the tens digit to be (b–3) ? Answer is we got 58 as the result.
Example 7
The present age of Sahil’s mother is three times the present age of Sahil. After 5 years their ages will add to 66 years. Find their present ages.
Assume present age of sahil be x then the
present age of his mother will be 3x.
After 5 years,
Sahil age =x+5
his mothers age =3x+5.
According to question
(x+5)+(3x+5)=66
4x+10=66
4x=56
x=14
So, the present age of sahil is 14 years and
his mother present age is 42 years.
Reducing Equations to Simpler Form
Bachcho agar linear equation fraction ki form mein given ho to hum usse en steps se simpler form mein reduce karte hai,
(i) Taking the LCM of the denominator
(ii) Multiply the LCM on both the sides, so that the number will reduce without the denominator and then open the brackets so that we can solve them by the balancing and transposing method.
Let's understand it more clearly through examples.
Example : Solve the linear equation
x2−13=x3+15
Solution :
Aap dekh sakte ho ki given equation complex form mein hai islie hum isse simpler form mein reduce karenge.
Step 1. Sare denominators 2,3 and 5
ka hume LCM lena hai which is 30.
Step 2. Hum equation ki dono sides ko 30 se multiply karenge.
30(x2−13)=30(x3+15)
⇒15x−10=10x+6
Steps 3.
Ab hum variables ko LHS mein aur constants ko RHS mein le jayenge.
15x−10x=6+10
⇒5x=16
Steps 4. Divide both side of equation by 5.
5x5=165
⇒x=3.2
Hence the solution of the given equation is x=165 or 3.2.
Example 8
Solve 5x−2(2x−7)=2(3x−1)+72.
Let us open the brackets,
LHS=5x–4x+14=x+14
RHS=6x−2+72=6x+32
The equation is x+14=6x+32
⇒14−32=6x−x [Transposing 32 to LHS and x to RHS]
⇒5x=252
⇒5x5=(252)×15 [Divide both sides by 5]
⇒x=52
Hence the required solution is 52.
Equations Reducible to the Linear Form
Bachcho kabhi kabhi aisa
bhi hota hai jab equations linear form mein nhi hoti lekin
hum unhe reduce karke linear equations ki form mein convert kar sakte hai aur jin methods ko abhi tak humne discuss kiya hai unse solve kar sakte hai.
Let's understand it more clearly through an example.
Example : Present ages of Anu and Raj are in the ratio 4:5. Eight years from now
the ratio of their ages will be 5:6. Find their present ages.
Solution : Bachcho maan lo ki anu ki present age 4x hai aur raj ki present agar 5x hai. Aap soch rhey honge ki humne 4x aur 5x hi kyon liya. Humne aisa islie lia kyonki unki age ka ratio 4:5 given hai.
After eight years. Anu’s age =(4x+8) years;
After eight years, Raj’s age =(5x+8) years.
∴ The ratio of their ages after eight years =4x+85x+8
This is given to be 5:6
∴ 56=4x+85x+8
Cross multiplication gives 6(4x+8)=5(5x+8)
or 24x+48=25x+40
or 24x+48–40=25x
or 24x+8=25x
or 8=25x–24x
or 8=x
Therefore, Anu’s present age =4x=4×8=32 years
Raj’s present age =5x=5×8=40 years
Example 9
Solve 8x−33x=2.
Observe that the equation is not a linear equation, since the expression on its
LHS is not linear. But we can put it into the form of a linear equation. We multiply both
sides of the equation by 3x,
8x−33x×3x=2×3x
⇒8x−3=6x
Transpose 6x to LHS and 3 to RHS, 8x−6x=3
⇒2x=3
Divide both sides of equation by 2,2x2=32
⇒x=32
Hence the solution of the equation is 32.
Example 10
The denominator of a rational number is greater than its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, the number obtained is 32 . Find the rational number.
Let numerator be x then denominator will be x+8.
According to question,
x+17x+7=32
⇒2(x+17)=3(x+7)
⇒2x+34=3x+21
⇒34−21=3x−2x
⇒13=x
⇒x=13
Required number is 1321.
Summary
- An algebraic equation is an equality involving variables. It says that the value of the expression on one side of the equality sign is equal to the value of the expression on the other side.
- The equations we study in Classes VI,VII and VIII are linear equations in one variable. In such equations, the expressions which form the equation contain only one variable. Further, the equations are linear, i.e., the highest power of the variable appearing in the equation is 1.
- A linear equation may have for its solution any rational number.
- An equation may have linear expressions on both sides. Equations that we studied in Classes VI and VII had just a number on one side of the equation.
- Just as numbers, variables can, also, be transposed from one side of the equation to the other.
- Occasionally, the expressions forming equations have to be simplified before we can solve them by usual methods. Some equations may not even be linear to begin with, but they can be brought to a linear form by multiplying both sides of the equation by a suitable expression.
- The utility of linear equations is in their diverse applications; different problems on numbers, ages, perimeters, combination of currency notes, and so on can be solved using linear equations.
Let's Revise
- Algebraic Equation :
(i) It is an equality involving variables. For example : 3x+6=4x−2 in which LHS is 3x+6, RHS is 4x−2 and equality is denoted by =
(ii) The value of the variable which satisfies the equation is its solution. - Linear Equation in one variable : Ye aisi algebraic equations hoti hai jiski degree 1 hoti hai aur sirf ek type ka variable hota hai.
- Solving Linear Equation In One Variable
Type 1 : Variable on one side and number on the other side.
(i) Balancing method : Es method mein hum balancing ko disturb na karte hue equation ki dono sides mein same number ko add, subtract, multiply ya divide karte hai.
(ii) Transposing method : Es method mein hum variables ya constants ko equation ki ek side se dusri side transpose ya transfer karte hai jab tak solution na mil jaye lekin transfer karte waqt apko yah dhyan rakhna hai ki jab hum kisi variable ya constant ko transfer karte hai to sign change ho jata hai. The changes are as follows :
(a) + changes to −
(b) − changes to +
(c)÷ changes to ×
(d)× changes to ÷
Type 2 : Variables and numbers on both sides.
Hum es type ki equations ko balancing method or transposing method se solve kar sakte hai. Apko ye dhyan rakhna hai ki transposing method variables per bhi applicable hota hai. - Reducing
Linear Equations To Simpler Form : Agar linear equation fraction ki form mein given ho to hum usse en steps se simpler form mein reduce karte hai,
(i) Taking the LCM of the denominator
(ii) Multiply the LCM on both the sides, so that the number will reduce without the denominator and then open the brackets so that we can solve them by the above methods. - Equations Reducible To Simpler Form : Jab equations linear form mein given na ho [Equation of the type 4x+85x+8=56] tab hum cross multiplication ka use karke unhe linear equations ki form mein reduce kar sakte hai.