घन और घनमूल कक्षा 8 गणित

Table Of Contents

भूमिका

अध्याय के शीर्षक के अनुसार इस अध्याय में हम घन और घनमूल का अध्ययन करेंगे। जब हम किसी संख्या को उसी संख्या से तीन बार गुणा करते हैं, तो प्राप्त संख्या उस संख्या का घन कहलाती हैं तथा घनमूल ज्ञात करना किसी संख्या का घन ज्ञात करने की प्रतिलोम संक्रिया है। इस अध्याय मे हम हार्डी रामानुजन संख्या, घन संख्याएँ, घन से संबंधित कुछ रोचक प्रतिरूप तथा घनमूल व इसको ज्ञात करने की विधियों का अध्ययन विस्तार से करेंगे।

आइये जानते है, घन और घनमूल को और करीब से...

पिछले अध्याय मे हमने वर्ग संख्याओं का अध्ययन किया हैं, जिसमे हम प्राकृत संख्याओं का स्वयं से गुणा करने पर देखते हैं कि :
$1 \times 1 = 1^{2} = 1$
$2 \times 2 = 2^{2} = 4$
$3 \times 3 = 3^{2} = 9$
$4 \times 4 = 4^{2} = 16$
$5 \times 5 = 5^{2} = 25$

अर्थात हम जानते हैं कि, जिस प्रकार $2 + 2$ को संक्षेप में $2 \times 2$ अर्थात $2^{2}$ लिखते हैं, उसी प्रकार $2 \times 2 \times 2$ को $2^{3}$ लिखते हैं तथा इसे 2 की घात 3 या 2 का घन पढ़ते हैं।

इसी प्रकार $3 \times 3 \times 3 = 3^{3}$ को 3 की घात 3 या 3 का घन पढ़ते हैं अर्थात् जब किसी संख्या का घातांक 3 होता है, तो प्राप्त होने वाली संख्या घन (CUBE) कहलाती है।

1 से 20 तक की प्राकृत संख्याओं के घन


संख्या	घन	संख्या	घन
$1$	$1$ $= (1 \times 1 \times 1 = 1^{3})$	$11$	$1331$ $= (11 \times 11 \times 11 = 11^{3})$
$2$	$8$ $= (2 \times 2 \times 2 = 2^{3})$	$12$	$1728$ $= (12 \times 12 \times 12 = 12^{3})$
$3$	$27$ $= (3 \times 3 \times 3 = 3^{3})$	$13$	$2197$ $= (13 \times 13 \times 13 = 13^{3})$
$4$	$64$ $= (4 \times 4 \times 4 = 4^{3})$	$14$	$2744$ $= (14 \times 14 \times 14 = 14^{3})$
$5$	$125$ $= (5 \times 5 \times 5 = 5^{3})$	$15$	$3375$ $= (15 \times 15 \times 15 = 15^{3})$
$6$	$216$ $= (6 \times 6 \times 6 = 6^{3})$	$16$	$4096$ $= (16 \times 16 \times 16 = 16^{3})$
$7$	$343$ $= (7 \times 7 \times 7 = 7^{3})$	$17$	$4913$ $= (17 \times 17 \times 17 = 17^{3})$
$8$	$512$ $= (8 \times 8 \times 8 = 8^{3})$	18	$5832$ $= (18 \times 18 \times 18 = 18^{3})$
$9$	$729$ $= (9 \times 9 \times 9 = 9^{3})$	$19$	$6859$ $= (19 \times 19 \times 19 = 19^{3})$
$10$	$1000$ $= (10 \times 10 \times 10 = 10^{3})$ $\frac{<}{t} d > < t d >$ 20 $\frac{<}{t} d > < t d >$ 8000=(20xx20xx20=20^3)

हार्डी रामानुजन संख्या

ऐसी संख्या जिसे दो घनों के योग के रूप मे भिन्न - भिन्न प्रकार से व्यक्त किया जा सकता है, हार्डी - रामानुजन संख्या कहलाती है।
उदाहरण के लिए :-
$1729 = 1728 + 1 = 12^{3} + 1^{3}$
$1729 = 1000 + 729 = 10^{3} + 9^{3}$

चूंकि $1729$ इस प्रकार की सबसे पहली और सबसे छोटी संख्या है इसलिए इसे सबसे छोटी हार्डी - रामानुजन संख्या कहा जाता है।

इस प्रकार की अनेक संख्याएँ होती है। जैसे :-
$4104 = 2^{3} + 16^{3}$ या $9^{3} + 15^{3}$
$13832 = 18^{3} + 20^{3}$ या $2^{3} + 24^{3}$

अतः इस प्रकार एक संख्या को दो घनों के रूप मे भिन्न - भिन्न प्रकार से व्यक्त करना ही हार्डी - रामानुजन संख्याएँ कहलाती है।

घन

सामान्यतः घनों का प्रयोग ज्यामिति मे किया जाता है। घन एक ऐसी ठोस आकृति होती है जिसकी सभी भुजाएँ समान होती है।
पूर्ण घन संख्याएँ :- किसी संख्या को उसी संख्या से तीन बार गुणा करने पर प्राप्त होने वाली संख्या पूर्ण घन संख्या कहलाती है। आइए एक सारणी से समझते है :-


संख्या	घन	संख्या	घन
$1$	$1$ $= (1 \times 1 \times 1 = 1^{3})$	$11$	$1331$ $= (11 \times 11 \times 11 = 11^{3})$
$2$	$8$ $= (2 \times 2 \times 2 = 2^{3})$	$12$	$1728$ $= (12 \times 12 \times 12 = 12^{3})$
$3$	$27$ $= (3 \times 3 \times 3 = 3^{3})$	$13$	$2197$ $= (13 \times 13 \times 13 = 13^{3})$
$4$	$64$ $= (4 \times 4 \times 4 = 4^{3})$	$14$	$2744$ $= (14 \times 14 \times 14 = 14^{3})$
$5$	$125$ $= (5 \times 5 \times 5 = 5^{3})$	$15$	$3375$ $= (15 \times 15 \times 15 = 15^{3})$
$6$	$216$ $= (6 \times 6 \times 6 = 6^{3})$	$16$	$4096$ $= (16 \times 16 \times 16 = 16^{3})$
$7$	$343$ $= (7 \times 7 \times 7 = 7^{3})$	$17$	$4913$ $= (17 \times 17 \times 17 = 17^{3})$
$8$	$512$ $= (8 \times 8 \times 8 = 8^{3})$	18	$5832$ $= (18 \times 18 \times 18 = 18^{3})$
$9$	$729$ $= (9 \times 9 \times 9 = 9^{3})$	$19$	$6859$ $= (19 \times 19 \times 19 = 19^{3})$
$10$	$1000$ $= (10 \times 10 \times 10 = 10^{3})$ $\frac{<}{t} d > < t d >$ 20 $\frac{<}{t} d > < t d >$ 8000=(20xx20xx20=20^3) $\frac{<}{t} d > \frac{<}{t} r > \frac{<}{t} a b \leq > < b r > उ प र ् य ु क ् त स ा र ण ी म े$ 1, 8, 27, ......, 8000 ये सभी संख्याएँ पूर्ण घन संख्याएँ है क्योंकि इन्हे संबंधित संख्या से तीन बार गुणा किया गया है। इस सारणी के अनुसार हम देख सकते है कि सम संख्याओं के घन सम संख्या तथा विषम संख्याओं के घन विषम संख्या होती है। उदाहरण 1 क्या $106480$ परिपूर्ण घन है ? 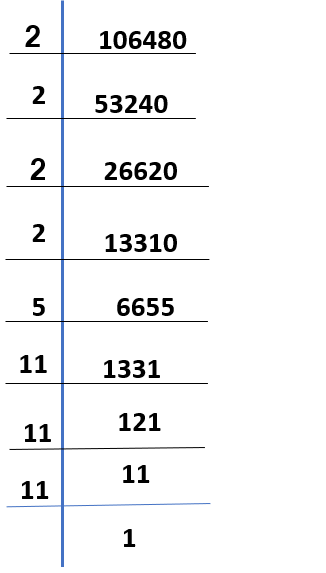$106480$ के अभाज्य गुणनखंड $= 2 \times 2 \times 2 \times 2 \times 5 \times 11 \times 11 \times 11$ $= 2^{4} \times 5 \times 11^{3}$ चूंकि हम जानते है कि पूर्ण घन होने के लिए वांछित संख्या के अभाज्य गुणनखंडों का तीन - तीन के समूह मे होना आवश्यक है। यहाँ केवल $11$ का त्रिक है। अतः यह संख्या पूर्ण घन संख्या नहीं है। Learn more उदाहरण 2 $5022$ के घन का इकाई का अंक ज्ञात कीजिए। चूंकि हम जानते है कि किसी संख्या के घन का अर्थ होता है उस संख्या का स्वयं से तीन बार गुणा। अर्थात ${(5022)}^{3}$ $= 5022 \times 5022 \times 5022$ हमे यहाँ इस संख्या के घन का इकाई का अंक ज्ञात करना है। परंतु इतनी बड़ी संख्या का गुणनफल ज्ञात करना बहुत कठिन होता है। अतः इसके लिए हमे इनके केवल इकाई के अंकों का गुणनफल ज्ञात करना है। $\Rightarrow 2 \times 2 \times 2 = 8$ अतः $5022$ के घन का इकाई का अंक $8$ होगा। Learn more घनों से संबंधित कुछ रोचक प्रतिरूप बच्चों! उपर्युक्त अध्ययन मे हमने कुछ प्राकृत संख्याओं के घनों तथा पूर्ण घन संख्याओं का अध्ययन किया है। अब हम घनों से संबंधित कुछ रोचक प्रतिरूपों का अध्ययन करेंगे। (i) क्रमागत विषम संख्याओं को जोड़ना : उपर्युक्त विधि से हमे यह ज्ञात होता है कि यदि हम क्रमागत विषम संख्याओं को जोड़ते है तो हमे अगली संख्या का घन प्राप्त होता है। (ii) घन और उनके अभाज्य गुणनखंड : किसी घन संख्या का अभाज्य गुणनखंडन करने के लिए उस संख्या के अभाज्य गुणनखंड करके उनको तीन - तीन के युग्म मे व्यवस्थित किया जाता है। यदि दी गई संख्या के सभी गुणनखंड तीन - तीन के युग्म मे हो तो वह संख्या पूर्ण घन संख्या कहलाती है। आइए एक उदाहरण से समझते है :- उदाहरण : क्या $216$ एक पूर्ण घन संख्या है ? 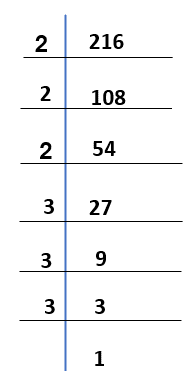हल : यहाँ हम देख सकते है कि $216$ के अभाज्य गुणनखंड $= 2 \times 2 \times 2 \times 3 \times 3 \times 3$ $= 2^{3} \times 3^{3} = {(2 \times 3)}^{3} = 6^{3}$ अतः $216$ संख्या $6$ का घन है। यदि इस संख्या के अभाज्य गुणनखंडों मे तीन - तीन के युग्म नहीं बनते तो यह संख्या पूर्ण घन संख्या नहीं होती। ऐसी स्थिति मे दी गई संख्या को एक ऐसी प्राकृत संख्या से गुणा किया जाता है जिससे कि उसके तीन - तीन के युग्म पूरे हो जाते है तथा वह पूर्ण घन संख्या के रूप मे प्राप्त होती है। उदाहरण : क्या $392$ एक पूर्ण घन संख्या है ? 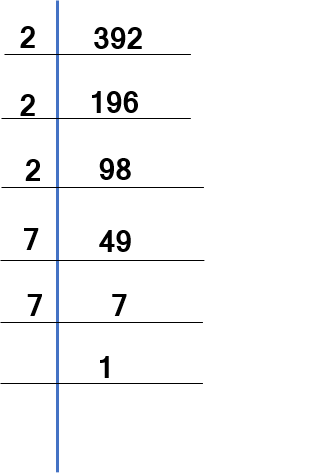जांच कीजिए। हल : यहाँ हम देख सकते है कि $392$ के अभाज्य गुणनखंड :- $= 2 \times 2 \times 2 \times 7 \times 7$ $= 2^{3} \times 7^{2}$ यहाँ $2$ का त्रिक तो बन रहा है किन्तु $7$ का त्रिक नहीं बन रहा है अतः $7$ का त्रिक बनाने अर्थात पूर्ण घन बनाने के लिए पूरी संख्या को $7$ से गुणा करने पर :- $= 392 \times 7$ $= 2 \times 2 \times 2 \times 7 \times 7 \times 7$ $= 2^{3} \times 7^{3}$ $= 14^{3} = 2744$ इस प्रकार हम सभी अपूर्ण संख्याओं का घन प्राप्त कर सकते है। OMR (One Minute Revision) जब किसी संख्या का घातांक 3 होता है, तो प्राप्त होने वाली संख्या घन (CUBE) कहलाती है। घनमूल ज्ञात करना किसी संख्या का घन ज्ञात करने की प्रतिलोम संक्रिया है। ऐसी संख्या जिसे दो घनों के योग के रूप मे भिन्न - भिन्न प्रकार से व्यक्त किया जा सकता है, हार्डी - रामानुजन संख्या कहलाती है। घन एक ऐसी ठोस आकृति होती है जिसकी सभी भुजाएँ समान होती है। किसी संख्या को उसी संख्या से तीन बार गुणा करने पर प्राप्त होने वाली संख्या पूर्ण घन संख्या कहलाती है। सम संख्याओं के घन सम संख्या तथा विषम संख्याओं के घन विषम संख्या होती है। उदाहरण 3 वह छोटी से छोटी संख्या कौन - सी है जिसमे $392$ को गुणा करने पर गुणनफल परिपूर्ण घन बन जाता है। अतः $392$ का गुणनखंड $= 2 \times 2 \times 2 \times 7 \times 7$ यहाँ $2$ का त्रिक बन रहा है किन्तु $7$ केवल दो बार ही आया है अतः इसका त्रिक बनाने के लिए दी गई संख्या को $7$ से गुणा करते है :- $392 \times 7 = 2744$ अब जो संख्या प्राप्त हुई है वह पूर्ण घन संख्या है क्योंकि यह संख्या $14$ का घन है। $\sqrt[3]{2744} = 14$ Learn more उदाहरण 4 निम्नलिखित संख्या को क्रमागत विषम संख्याओं के योग के रूप में व्यक्त कीजिए : $6^{3}$ $6^{3} = 6 \times 6 \times 6$ $= 36 \times 6$ $= 216$ क्रमागत विषम संख्याओं के योग के रूप मे :- $= 31 + 33 + 35 + 37 + 39 + 41$ $= 216$ Learn more उदाहरण 5 राज ने प्लास्टिसिन का एक घनाभ बनाया इस घनाभ की लम्बाई चौड़ाई और ऊँचाई क्रमशः $15$ cm, $30$ cm और $15$ cm है। अनु उससे पूछती है कि एक (पूर्ण) घन बनाने के लिए उसे ऐसे कितने घनाभों की आवश्यकता होगी ? चूंकि हमे यहाँ दिया गया है :- लंबाई $l = 15$ cm चौड़ाई $b = 30$ cm ऊंचाई $h = 15$ cm घनाभ का आयतन $= l \times b \times h$ $= 15 \times 30 \times 15$ $= 15 \times 15 \times 2 \times 15$ $= 15 \times 15 \times 15 \times 2$ चूंकि यहाँ पूर्ण घन प्राप्त करने के लिए $2$ का त्रिक भी बनाना होगा अतः इसे $2 \times 2$ अर्थात $4$ से गुणा करने की आवश्यकता है। अतः पूर्ण घन बनाने के लिए ऐसे $4$ घनाभों की आवश्यकता होगी। Learn more उदाहरण 6 वह सबसे छोटी संख्या ज्ञात कीजिए जिसे निम्नलिखित संख्या मे भाग देने पर भागफल एक पूर्ण घन प्राप्त हो जाए : $256$ $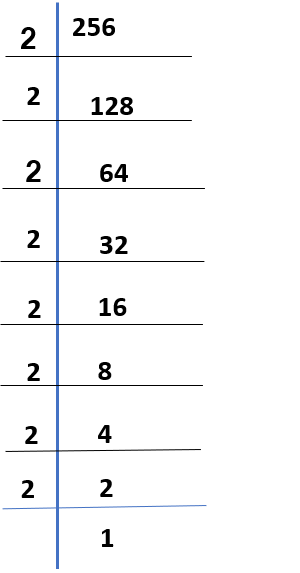256$ के अभाज्य गुणनखंड $= 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$ $= 2^{8}$ $= 2^{3} \times 2^{3} \times 2^{2}$ (चूंकि गुणा मे घाते जुड़ जाती है।) यहाँ प्रथम दो का त्रिक बन रहा है परंतु तीसरे का त्रिक नहीं बन रहा है अतः इसका दी गई संख्या मे भाग देते है :- $= \frac{256}{2^{2}}$ $= \frac{256}{4}$ $= 64$ $= 2^{3} \times 2^{3}$ अतः $256$ मे $4$ का भाग देने पर $64$ प्राप्त होता है जो एक पूर्ण घन संख्या है। Learn more घनमूल और इसके ज्ञात करने की विधियाँ जिस प्रकार वर्गमूल ज्ञात करना वर्ग प्राप्त करने की प्रतिलोम संक्रिया है, उसी प्रकार घनमूल ज्ञात करना भी घन प्राप्त करने की प्रतिलोम संक्रिया है। हम जानते है कि $2^{3} = 8$ होता है इसलिए हम कहते है कि $8$ का घनमूल $2$ है। अतः इसे हम $\sqrt[3]{8} = 2$ लिखते है। घनमूल का प्रतीक $= \sqrt[3]{x}$ $\Rightarrow$ यहाँ $x$ वह संख्या है जिसका हमे घनमूल ज्ञात करना होता है। घनमूल ज्ञात करने की विधियाँ (i) अभाज्य गुणनखंड विधि : इस विधि से घनमूल निम्न प्रकार ज्ञात किया जाता है :- चरण 1: सर्वप्रथम दी गई संख्या के अभाज्य गुणनखंड लिखते है। चरण 2: फिर उनके तीन - तीन के युग्म बनाते है । चरण 3: उन युग्मों मे से एक - एक अंक लेते है। चरण 4: अंत मे उन एकल अंकों का गुणा करते है तथा जो गुणनफल प्राप्त होता है वही उस संख्या का घनमूल होता है। आइए एक उदाहरण से समझते है:- उदाहरण : $8000$ का घनमूल ज्ञात कीजिए। 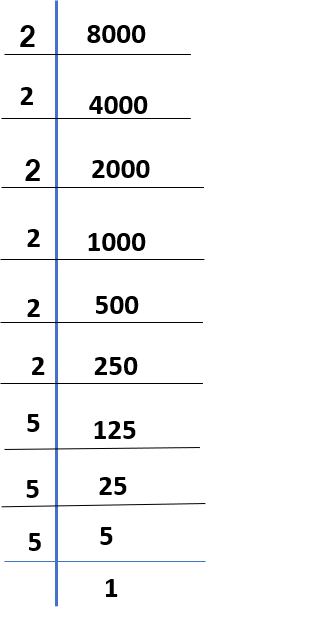अतः $8000$ के गुणनखंड $= 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 5$ तीन - तीन के युग्म बनाने पर $= (2 \times 2 \times 2) \times (2 \times 2 \times 2) \times (5 \times 5 \times 5)$ $= 2 \times 2 \times 5 = 20$ अतः $8000$ का घनमूल $20$ होगा। (ii) आकलन विधि : घनमूल ज्ञात करने की यह विधि अनुमान पर आधारित है। आइए इसे एक उदाहरण की सहायता से समझते है :- उदाहरण : संख्या $857375$ का घनमूल ज्ञात कीजिए। हल : चरण 1: सर्वप्रथम इसके दाईं ओर के अंक से प्रारंभ करते हुए तीन - तीन अंकों के समूह बनाते है। $\Rightarrow 875$ (दूसरा समूह) $; 375$ (पहला समूह) चरण 2: पहला समूह $375$ से हमे वांछित घनमूल का इकाई का अंक प्राप्त होगा। $\Rightarrow$ क्योंकि हम जानते है कि किसी संख्या के इकाई के अंक के स्थान पर $5$ तब आता है जब उसके घनमूल का इकाई का अंक $5$ होता है। अतः पहले समूह से हमे वांछित घनमूल का इकाई का अंक $5$ प्राप्त हुआ। चरण 3: अब दूसरे समूह को लेते है। हम जानते है कि $9^{3} = 729$ तथा $10^{3} = 1000$ होता है। दूसरा समूह इन दोनों संख्याओं के घनों के बीच मे है अतः इस स्थिति मे हमेशा छोटी संख्या अर्थात $9$ के इकाई के अंक $9$ को वांछित घनमूल के दहाई अंक के रूप मे लेते है। $\Rightarrow$ अतः वांछित घनमूल का दहाई अंक $= 9$ इस प्रकार हमे $857375$ का घनमूल $95$ प्राप्त होता है। अर्थात $\sqrt[3]{857375} = 95$ नोट : इस प्रक्रिया मे दी गई संख्या के घन मे सर्वप्रथम तीन अंकों का समूह ही बनाते है। उसके बाद यदि पर्याप्त अंक हो तो तीन अंकों का समूह बनाते है अपितु दो अंकों का समूह बनाकर इसी प्रकार घनमूल ज्ञात किया जाता है। उदाहरण 7 निम्नलिखित का मान ज्ञात कीजिए। $\sqrt[3]{125 \times 216}$ चूंकि हमे दिया गया है :- $= \sqrt[3]{125 \times 216}$ $= \sqrt[3]{(5 \times 5 \times 5) \times (6 \times 6 \times 6)}$ $= \sqrt[3]{(5^{3}) \times (6^{3})}$ $= 5 \times 6$ $= 30$ Learn more उदाहरण 8 अभाज्य गुणनखंड विधि द्वारा निम्नलिखित संख्या का घनमूल ज्ञात कीजिए : $110592$ अतः $110592$ के अभाज्य गुणनखंड $= 2^{3} \times 2^{3} \times 2^{3} \times 2^{3} \times 3^{3}$ $110592$ का घनमूल $= 2 \times 2 \times 2 \times 2 \times 3 = 48$ Learn more उदाहरण 9 अभाज्य गुणनखंडन का उपयोग करके निम्नलिखित संख्या के घनमूल ज्ञात कीजिए : $970299$ अतः $970299$ के अभाज्य गुणनखंड $= 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 11 \times 11 \times 11$ $970299$ का घनमूल $= (3 \times 3 \times 3) \times (3 \times 3 \times 3) \times (11 \times 11 \times 11)$ $= 3 \times 3 \times 11 = 99$ $= \sqrt[3]{970299} = 99$ Learn more उदाहरण 10 निम्नलिखित पूर्ण घन संख्या का घनमूल आकलन द्वारा ज्ञात कीजिये- $17576$ चरण 1: सर्वप्रथम इसके दाईं ओर के अंक से प्रारंभ करते हुए तीन - तीन अंकों के समूह बनाते है। $\Rightarrow 17$ (दूसरा समूह) $; 576$ (पहला समूह) चरण 2: पहला समूह $576$ से हमे वांछित घनमूल का इकाई का अंक प्राप्त होगा। अतः पहले समूह से हमे वांछित घनमूल का इकाई का अंक $6$ प्राप्त हुआ। चरण 3: अब दूसरे समूह को लेते है। हम जानते है कि $2^{3} = 8$ तथा $3^{3} = 27$ होता है। दूसरा समूह इन दोनों संख्याओं के घनों के बीच मे है अतः इस स्थिति मे हमेशा छोटी संख्या के अर्थात $2$ के इकाई के अंक $2$ को वांछित घनमूल के दहाई अंक के रूप मे लेते है। $\Rightarrow$ अतः वांछित घनमूल का दहाई अंक $= 2$ इस प्रकार हमे $17576$ का घनमूल $26$ प्राप्त होता है। अर्थात $\sqrt[3]{17576} = 26$ Learn more सारांश $1729, 4104, 13832$ जैसी संख्याएँ हार्डी - रामानुजन संख्याएँ कहलाती है क्योंकि इन्हे दो घनों के योग के रूप मे भिन्न - भिन्न प्रकारों से व्यक्त किया जा सकता है। एक संख्या को स्वयं से तीन बार गुणा करने पर प्राप्त होने वाली संख्या घन संख्या कहलाती है। किसी संख्या के अभाज्य गुणनखंड मे प्रत्येक गुणनखंड तीन बार आता है तो वह संख्या एक पूर्ण घन संख्या कहलाती है। घनमूल का चिह्न $= \sqrt[3]{x}$ होता है। $\Rightarrow$ जहाँ $x$ वह संख्या होती है जिसका हमे घनमूल ज्ञात करना होता है। Exams IIT JEE NEET UP Board Bihar Board CBSE Free Textbook Solutions KC Sinha Solutions for Maths Cengage Solutions for Maths DC Pandey Solutions for Physics HC Verma Solutions for Physics Sunil Batra Solutions for Physics Pradeep Solutions for Physics Errorless Solutions for Physics Narendra Awasthi Solutions for Chemistry MS Chouhan Solutions for Chemistry Errorless Solutions for Biology Free Ncert Solutions English Medium NCERT Solutions NCERT Solutions for Class 12 English Medium NCERT Solutions for Class 11 English Medium NCERT Solutions for Class 10 English Medium NCERT Solutions for Class 9 English Medium NCERT Solutions for Class 8 English Medium NCERT Solutions for Class 7 English Medium NCERT Solutions for Class 6 English Medium Free Ncert Solutions Hindi Medium NCERT Solutions NCERT Solutions for Class 12 Hindi Medium NCERT Solutions for Class 11 Hindi Medium NCERT Solutions for Class 10 Hindi Medium NCERT Solutions for Class 9 Hindi Medium NCERT Solutions for Class 8 Hindi Medium NCERT Solutions for Class 7 Hindi Medium NCERT Solutions for Class 6 Hindi Medium Boards CBSE UP Board Bihar Board UP Board Resources Unit Converters Calculators Books Store Seminar Results Search Doubtnut Blogs Class 12 All Books Class 11 All Books Class 10 All Books Class 9 All Books Class 8 All Books Class 7 All Books Class 6 All Books Doubtnut is No.1 Study App and Learning App with Instant Video Solutions for NCERT Class 6, Class 7, Class 8, Class 9, Class 10, Class 11 and Class 12, IIT JEE prep, NEET preparation and CBSE, UP Board, Bihar Board, Rajasthan Board, MP Board, Telangana Board etc NCERT solutions for CBSE and other state boards is a key requirement for students. Doubtnut helps with homework, doubts and solutions to all the questions. It has helped students get under AIR 100 in NEET & IIT JEE. Get PDF and video solutions of IIT-JEE Mains & Advanced previous year papers, NEET previous year papers, NCERT books for classes 6 to 12, CBSE, Pathfinder Publications, RD Sharma, RS Aggarwal, Manohar Ray, Cengage books for boards and competitive exams. Doubtnut is the perfect NEET and IIT JEE preparation App. Get solutions for NEET and IIT JEE previous years papers, along with chapter wise NEET MCQ solutions. Get all the study material in Hindi medium and English medium for IIT JEE and NEET preparation Contact Us ALLEN CAREER INSTITUTE PRIVATE LIMITED, Plot No. 13 & 14, Dabra Road, Sector 13, Hisar, Haryana 125001 info@doubtnut.com Terms & Conditions \| Payment Terms \| Privacy Policy \| Contact Us \| About Us \| ©2024 Copyright @Doubtnut Home Ask Doubt Profile