गति एवं समय कक्षा 7 विज्ञान
भूमिका
पिछली कक्षाओं में आपने गति के बारे में पढ़ा होगा कि गति क्या होती है ? गति के कितने प्रकार होते हैं ? क्या आप दूरी एवं चाल के बारे में जानते है तथा समय के साथ इनका मापन कर सकते हैं ? तो बच्चों आज हम इस अध्याय में गति, चाल एवं समय के मापन के बारे में जानेंगे। साथ ही इनसे जुड़े सभी तथ्यों के बारे में भी चर्चा करेंगे।
आपने ग्राफ देखा है ? इस अध्याय में हम ग्राफ के बारे में जानेंगे तथा ग्राफ बनाना भी सीखेंगे।
गति
जब कोई वस्तु समय के साथ अपने आसपास के वस्तुओं की अपेक्षा अपनी अवस्था या स्थिति में परिवर्तन करती है, तो इसे उस वस्तु की गति कहते हैं। गति को हम किसी वस्तु की अवस्था में परिवर्तन भी कह सकते हैं। कक्षा 6वीं में हमने गति के प्रकारों के बारे में पढ़ा था। क्या आपको कुछ याद है ? यदि नहीं तो चलिए उन्हें दोहरा लेते हैं -
गति के प्रकार : गति मुख्यतः 6 प्रकार की होती है, जो निम्न हैं -
आइए गति के प्रकारों के बारे में जानें -
सरल रेखीय गति : जब कोई वस्तु एक सीधी रेखा या सीधे पथ में गति करती है, तो वस्तु की उस गति को सरल रेखीय गति कहते हैं। सरल रेखीय गति के उदाहरण - सड़क पर चलते वाहन की गति, मैदान में मार्च पास्ट करते सैनिकों की गति, ब्लैक बोर्ड पर एक सीधी रेखा खींचना आदि सभी सरल रेखीय गति के उदाहरण हैं।

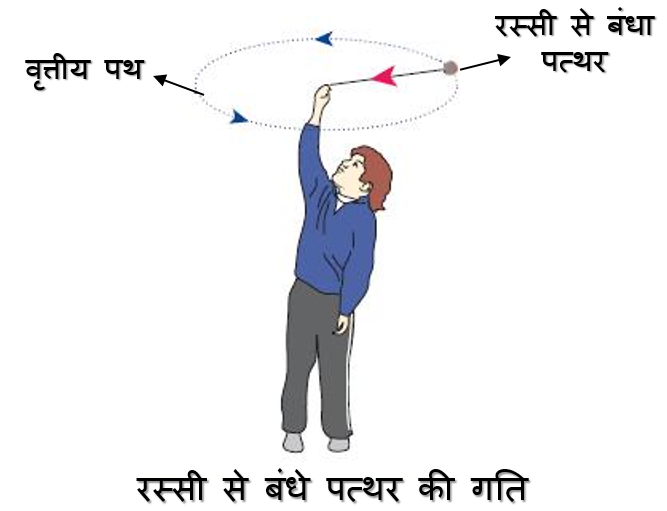
वर्तुल गति : जब कोई वस्तु किसी वृत्ताकार मार्ग में गति करती है तथा केंद्र से उस वस्तु की दूरी समान रहती है, तो उस वस्तु की गति को वर्तुल गति कहते हैं। उदाहरण - घड़ी में लगी सुइयों की गति वर्तुल गति होती है, किसी रस्सी से बंधे पत्थर को घूमाना वर्तुल गति ही है, पंखे के ब्लेड का घूमना आदि।
घूर्णन गति : जब कोई गतिशील वस्तु अपने अक्ष के चारों ओर घूमती हैं, तो उस वस्तु की गति को घूर्णन या घूर्णी गति कहते हैं। उदाहरण - लट्टू की गति, पृथ्वी के अपने अक्ष के चारों ओर घूमने की गति, मिट्टी के बर्तन बनाने वाले चाक की गति आदि घूर्णन गति के उदाहरण हैं।

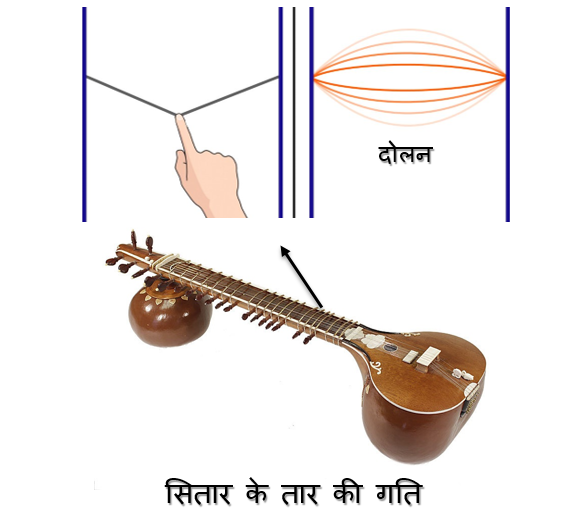
दोलन गति : जब कोई वस्तु अपनी स्थिर अवस्था से अगल-बगल या ऊपर-नीचे गति करता है, तो वस्तु की इस गति को दोलन गति कहते हैं। उदाहरण - सरल लोलक या पेंडुलम तो आपने देखा ही होगा कि उसमें किस प्रकार दाएं-बाएं गति होती है, इसी प्रकार लटकती हुई घंटी की गति तथा सितार में लगे तार की गति भी दोलन गति के उदाहरण हैं।
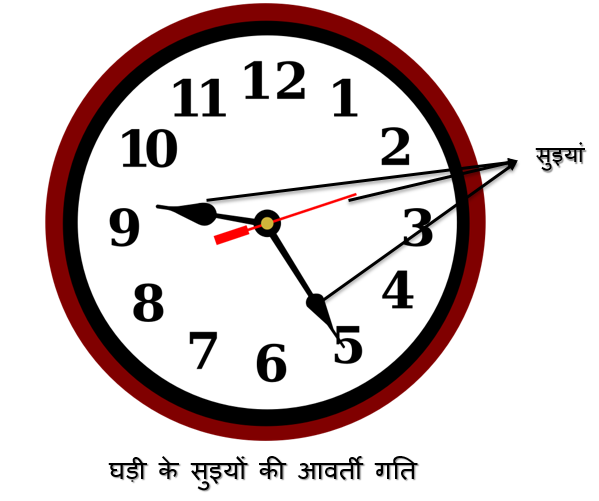
आवर्ती गति : किसी वस्तु की वह गति जो एक निश्चित समय के बाद दोहराई जाती है, उसे आवर्ती गति है। आवर्ती गति को दोहराने का समय निश्चित होता है। जैसे - घड़ी की सुइयां जिसमें सेकंड वाली सुई 60 सेकंड के पश्चात पुनः अपनी गति को दोहराती है।
अनावर्ती गति : किसी वस्तु की वह गति जिसमें वह वस्तु अपनी गति को दोहराती है, परंतु इसका कोई निश्चित समय नहीं होता है, ऐसी गति को अनावर्ती या अनियमित गति कहते हैं। अतः हम यह भी कह सकते हैं कि वह गति जो आवर्ती नहीं होती, उन्हें अनावर्ती गति कहते हैं। उदाहरण - आकाश में उड़ने वाले पक्षियों की गति, फुटबाल के मैदान में भागते खिलाड़ियों की गति, पतंग की गति आदि अनावर्ती गति के उदाहरण हैं।

मंद अथवा तीव्र गति
हम गति एवं उसके प्रकारों के बारे में तो जान चुके हैं, परंतु क्या आप यह जानते हैं कि क्या सभी वस्तुएँ एक समान ही गतिमान होती है ? नहीं ऐसा नहीं है। कुछ वस्तुओं की गति धीमी या मंद होती है अर्थात कुछ वस्तुएँ धीरे-धीरे गति करती है। ऐसी गति को मंद गति कहते हैं। जैसे - कछुए की गति। आपने कछुआ तो देखा ही होगा। कछुआ बहुत ही धीमी गति से चलता है, अतः वह मंद गति करता है।

आपने खरगोश और कछुए की कहानी तो सुनी ही होगी, जिसमें खरगोश बहुत ही तेज गति से चलने के कारण थक जाता है एवं कछुआ धीमी गति करता है। अतः इससे जान सकते हैं कि सभी वस्तुओं में एक समान गति नहीं होती है। कुछ वस्तुओं में तेज गति होती है, तो कुछ वस्तुओं में मंद गति होती है। जिन वस्तुओं में तीव्र गति होती हैं, उनकी चाल अधिक होती है।
हम यह कैसे ज्ञात करेंगे कि कोई वस्तु मंद गति में है या तीव्र गति में है ? इसके लिए हम उस गतिशील वस्तु की तुलना अन्य गतिशील वस्तुओं से करके यह बता सकते हैं कि कौन सी वस्तु तीव्र गति में है या मंद गति में है। जैसे - सड़क पर चलते वाहनों का अवलोकन करने पर हमें पता चलता है कि कुछ वाहन धीरे-धीरे चलते हैं तथा कुछ वाहन उन धीरे वाहनों को पीछे छोड़कर आगे बढ़ जाते हैं। जो वाहन अन्य वाहनों से आगे बढ़ जाते हैं, वह तीव्र गति से चलते हैं।
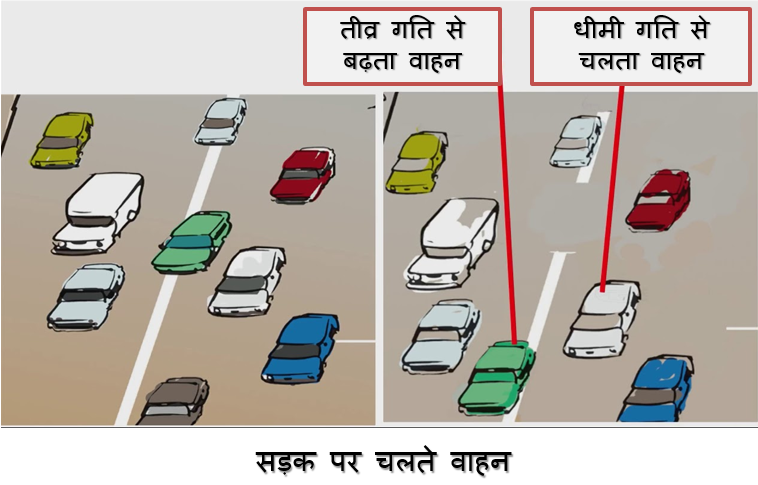
मंद एवं तीव्र गति के सही पहचान के लिए हमें एक निश्चित समय में वस्तुओं द्वारा तय की गई कुल दूरी का ज्ञात होना भी आवश्यक है क्यूंकी जो वस्तु कम समय में अधिक दूरी तय करती है, उसकी गति तीव्र होती है। किसी भी एक स्थान से दूसरे स्थान के बीच की लंबाई को उनके बीच की दूरी कहते हैं।
समय
किन्ही दो घटनाओं के बीच के काल-अंतर (अंतराल) को समय कहा जाता है, इसे इस प्रकार भी कह सकते हैं कि किसी गतिशील बिंदु के द्वारा एक बिन्दु से दूसरे बिन्दु तक जाने के अंतराल को समय कहते हैं। यह एक भौतिक राशि होती है। हम अपने प्रतिदिन के सभी कार्य समय देख कर ही करते हैं। समय एक निरंतर चलने वाली राशि है, अतः समय को कभी रोका नहीं जा सकता है। परंतु हम समय का मापन कर सकते हैं।
समय का मात्रक : बच्चों क्या आप समय के मूल मात्रक के बारे में जानते है ? समय का मूल मात्रक होता है - सेकंड। सेकंड को s से प्रदर्शित करते हैं। सेकंड समय का छोटा मात्रक है, मिनट (min) तथा घण्टा (hr) समय के बड़े मात्रक हैं। क्या आप जानते हैं कि यह एक दूसरे से कैसे संबंधित होते हैं ? आइए जानें -
60 सेकंड = 1 मिनट
60 मिनट = 1 घण्टा
24 घण्टे = 1 दिन
7 दिन = 1 सप्ताह
365 दिन = 12 मास (महीने)
12 महीने = 1 वर्ष
सभी मूल मात्रकों के प्रतीक चिन्हों को हमेशा एकवचन में ही लिखा जाता है, बहुवचन में कभी नहीं लिखा जाता। जैसे - 50 km लिखा जाता है न की 50 kms। अलग-अलग जगह आवश्यकता एवं परिस्थिति के अनुसार समय के मात्रकों का उपयोग किया जाता है। जैसे - जहाँ समय के छोटे अंतराल का माप बताना होता है, वहाँ समय के छोटे मात्रक सेकंड (s) का उपयोग किया जाता है तथा जहाँ समय के बड़े अंतराल को बताया जाता है वहाँ मिनट, घण्टे, दिन, महीने, वर्ष का उपयोग किया जाता है। किसी व्यक्ति की आयु को बताने के लिए वर्ष का उपयोग किया जाता है, क्यूंकी यह बड़ा काल अंतर होता है।
समय मापन की तकनीक
समय के मापन से आशय केवल सेकंड, मिनट व घण्टे के मापन से नहीं है। समय के मापन से आशय एक दिन में होने वाले कुल घण्टे, एक सप्ताह में दिनों की संख्या, एक महीने में दिन एवं सप्ताह तथा एक वर्ष में कुल दिनों तथा महीनों की संख्या से है। आज के युग में समय के मापन के लिए विभिन्न प्रकार की घड़ियाँ एवं कैलेन्डर उपयोग में लाए जाते है, परंतु क्या आप जानते हैं कि पुराने समय में जब घड़ियों का आविष्कार नहीं हुआ था, तब हमारे बुजुर्ग किस प्रकार समय का मापन करते थे ?
समय मापन की पुरानी विधियाँ : पुराने समय में आज के समान विशेष प्रकार के समय मापन की युक्तियाँ नहीं थी, फिर भी वे सूरज की सहायता से समय का मापन किया करते थे। उन्होंने जाना कि प्रकृति में कुछ घटनाएँ एक निश्चित समय के बाद अपने आप दोहराती है। जैसे - प्रतिदिन सूर्य उदय होता है तथा डूबता है, इसके बीच के समय को दोपहर कहा गया एवं जब सूरज के डूबने से लेकर उसके उदय होने तक के अंतराल को रात्रि कहा गया। दोनों घटनाओं को एक पूरा दिन कहा जाने लगा।

ठीक इसी प्रकार एक अमावस्या (जब चंद्रमा दिखाई नहीं देता) से लेकर अगली अमावस्या तक के अंतराल को एक माह का समय नियत किया गया। अमावस्या वह घटना है, जब चंद्रमा पृथ्वी के पीछे की ओर चला जाता है तथा दिखाई नहीं देता। ऐसा चंद्रमा के पृथ्वी की परिक्रमा करने के कारण होता है एवं परिक्रमा पूर्ण होने के बाद चंद्रमा दिखाई देने लगता है। यह निरंतर चलते रहता है। चंद्रमा के समान पृथ्वी भी सूर्य की परिक्रमा करती है। जब पृथ्वी सूर्य की एक परिक्रमा पूर्ण करती है, तो इस समय को एक वर्ष के रूप में मापा जाता है।
दिन, माह तथा वर्ष ये सभी समय के बड़े मापन को दर्शाते हैं, अतः हमें इनसे बहुत छोटे समय के मापन की आवश्यकता भी होती है। जिनके लिए समय के मापन की अलग-अलग विधियाँ एवं उपकरण होते हैं। जैसे - रेत-घड़ी, धूप-घड़ी, जल-घड़ी ये सभी पहले के समय मापन के उपकरण थे। विश्व के अलग-अलग स्थानों में इनके डिजाइन अलग-अलग थे। नीचे चित्र में इन्हें देखा जा सकता है। इनमें से कुछ आपने टीवी या फिल्मों में भी देखा होगा।
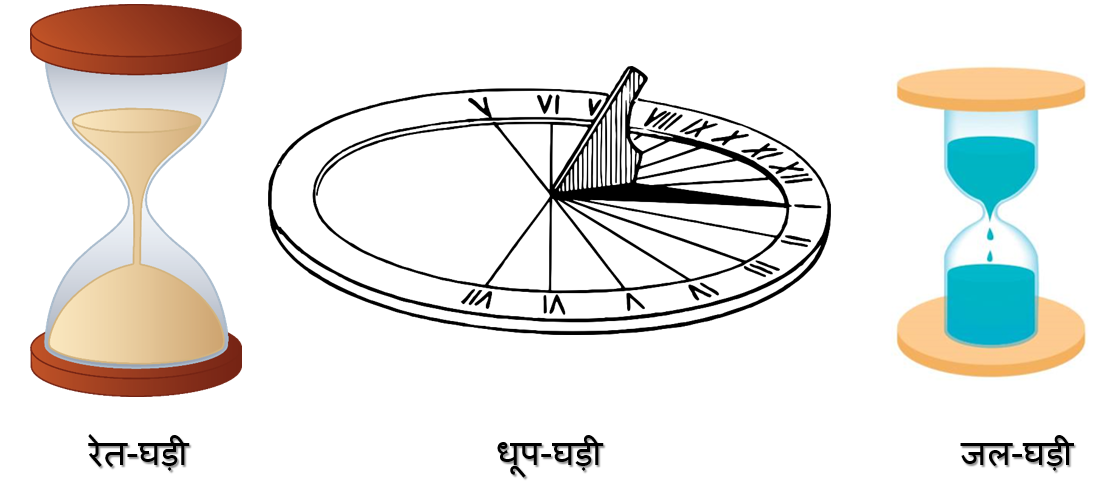
समय मापन की आधुनिक विधियाँ : आज के युग में समय मापन के यंत्रों को तो हम सभी जानते ही हैं। हम सभी अपनी कलाइयों में रंग बिरंगी घड़ियाँ पहनते हैं। आधुनिक समय में अनेक प्रकार की घड़ियाँ विकसित हो चुकी हैं। जिनमें से बहुत सी घड़ियाँ विद्युत सेल से चलती है, इनमें से कुछ नीचे चित्र में देखे जा सकते हैं। घड़ियों की सहायता से हम एक दिन के छोटे से छोटे अंतराल का मापन कर सकते हैं। कुछ घड़ियों के द्वारा समय के बहुत ही छोटे भाग को भी मापा जा सकता है। जैसे - एक माइक्रोसेकंड एक सेकंड का 10 लाखवाँ भाग होता है तथा एक नैनोसेकंड एक सेकंड का एक अरबवाँ भाग होता है। ऐसी घड़ियों का उपयोग वैज्ञानिक कार्यों के लिए किया जाता है।

घड़ी की आंतरिक बनावट बहुत ही जटिल होती है, अतः इसे समझना कठिन है, परंतु सभी घड़ियों में एक ही प्रकार की गति होती है, “आवर्ती गति”। आवर्ती गति के बारे में तो आप सभी जानते ही हैं। आवर्ती गति का एक सबसे अच्छा उदाहरण सरल लोलक (पेंडुलम) है।
सरल लोलक (पेंडुलम)
सरल लोलक आप सभी ने देखा ही होगा। कुछ पुरानी घड़ियों में भी सरल लोलक देखा जा सकता है। यह एक धागे से लटका एक धातु का गोलक होता है, जिसे स्वतंत्रता पूर्वक लटकाकर एक ओर खींचकर छोड़ने से वह दाएं एवं बाएं दोलन गति करता है। इसमें दोलन गति एवं आवर्ती गति दोनों होती है। धातु के गोले को लोलक का गोलक कहते हैं।
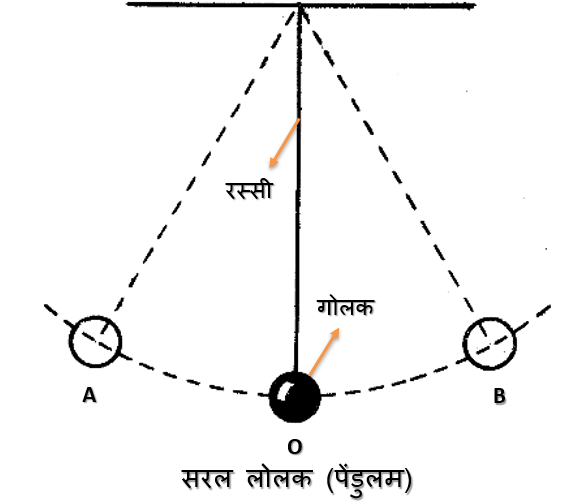
ऊपर चित्र में देखा जा सकता है कि एक सरल लोलक को किसी दीवाल या स्टैंड में लटकाया जाता है एवं स्थिर अवस्था में तीन बिन्दु बनाए जाते हैं - A, O तथा B। जहाँ O को गोलक का स्थिर बिन्दु या प्रारम्भिक बिन्दु माना जाता है। चित्र में दिखाए अनुसार जब लोलक को गति कराया जाता है, तो वह O से A तक तथा A से B तक फिर B से O में वापस आता है, इस प्रकार सरल लोलक का एक दोलन पूर्ण होता है।
आवर्तकाल : सरल लोलक जीतने समय में अपना एक दोलन पूरा करता है, उसे उस सरल लोलक का आवर्तकाल कहते हैं। किसी सरल लोलक का आवर्तकाल ज्ञात करने के लिए हमें विराम घड़ी (स्टॉप वॉच) की आवश्यकता होती है। यदि विराम घड़ी नहीं है, तो सामान्य दीवाल घड़ी या कलाई घड़ी का भी उपयोग कर सकते हैं। आवर्तकाल ज्ञात करने की विधि को नीचे उदाहरण द्वारा समझा जा सकता है।
उदाहरण - एक सरल लोलक लेते है तथा उसे एक स्टैंड या दीवाल में कील की सहायता से लटका लेते हैं। दोलन के मापन के लिए उसके नीचे प्रारम्भिक बिन्दु बना लेते हैं, जिससे हमें यह ज्ञात करने में आसानी होगी कि लोलक द्वारा एक दोलन पूर्ण कर लिया गया है।
अब सरल लोलक को दोलन कराना प्रारंभ करते है तथा समय नोट कर लेते हैं। इसे एक बार गति कराकर छोड़ देते हैं तथा इसके द्वारा पूर्ण किए गए कुल दोलनों की संख्या नोट कर लेते हैं। जैसे - इसे 20 बार दोलन कराते है एवं 20 दोलनों में लगे समय को नोट कर लेते हैं। मान लीजिए इसे 20 दोलनों में 42 सेकंड लगता है। अब एक दोलन में लगा समय या आवर्तकाल निकालने के लिए 20 दोलनों में लगे कुल समय को 20 से भाग दे देते हैं। इससे हमारा आवर्तकाल निकल जाता है।
20 दोलन पूरा करने में लगा समय = 42 सेकंड
1 दोलन पूरा करने में लगा समय =
= 4220 = 2.1 सेकंड
एक दोलन में 2.1 सेकंड का समय लगता है,अतः सरल लोलक का आवर्तकल 2.1 सेकंड होगा।
चाल
एक निश्चित समय में किसी वस्तु द्वारा तय की गई कुल दूरी को उस वस्तु की चाल कहते हैं। चाल का मात्रक मीटर (m) प्रति सेकंड (s) होता है। यह मीटर (m) प्रति मिनट (min) या मीटर (m) प्रति घण्टा (h) भी हो सकता है। चाल किसी भी वस्तु के द्वारा एकांक समय में तय की गई कुल दूरी का मान होता है। अतः चाल को निम्न सूत्र से ज्ञात किया जा सकता है -

उपरोक्त सूत्र की सहायता से हम किसी भी गतिशील वस्तु की चाल निकाल सकते हैं। जैसे यदि कोई वाहन 1 घण्टे में 60 किलोमीटर की दूरी तय करता है, तो उसकी चाल 60 किलोमीटर प्रति घण्टा होगी। परन्तु इससे यह स्पष्ट नहीं होता की वह वाहन एक घण्टे तक एक नियत चाल से चलता है क्यूंकि कोई भी वाहन एक धीमी गति से आरम्भ होकर अपनी चाल को बढ़ाता है। अतः किसी वाहन के 60 किलोमीटर प्रति घण्टा की चाल से आशय केवल उस वाहन के द्वारा 1 घण्टे में तय की गयी कुल दूरी से होता है। हम केवल वाहन की औसत चाल के बारे में ही बात करते हैं। हम इस पर ध्यान नहीं देते की वाहन 1 घण्टे तक एक ही गति से चलती है या नहीं।
चाल के प्रकार
चाल प्रायः दो प्रकार की होती है -
असमान चाल : यदि किसी सरल रेखा के अनुदिश गति करने वाली वस्तु की चाल परिवर्तित होती रहे, तो उस चाल को वस्तु की असमान चाल कहते हैं। जैसे - आकाश में उड़ता पक्षी, स्टेशन से छूटती रेलगाड़ी।
समान चाल : यदि किसी सरल रेखा के अनुदिश वस्तु नियत चाल से गति करती रहे, तो उस वस्तु की चाल को एक समान चाल कहते हैं। जैसे - पृथ्वी की गति एवं घड़ी के पैण्डुलम की गति।
चाल का मापन
हम समय के मापन के बारे में जान ही चुके हैं तथा हम दूरी के बारे में भी जानते हैं। समय तथा दूरी की सहायता से हम किसी गतिशील वस्तु की चाल जान सकते हैं। जैसा के हम जानते हैं कि चाल का मात्रक मीटर प्रति सेकंड (m/s) होता है। क्या आप जानते हैं कि यदि किसी वस्तु की चाल किलोमीटर प्रति घण्टे (km/h) में दी हो, तो उसे m/s में कैसे परिवर्तित करेंगे ? आइए इसे एक उदाहरण के द्वारा समझते हैं -
उदाहरण - यदि किसी वस्तु की चाल 360 km/h दी गई है, अब इसे m/s में परिवर्तित करते हैं। इसके लिए हमें किलोमीटर को मीटर में बदलना होगा तथा घण्टे को सेकंड में बदलना होगा।
जैसा के हम जानते हैं कि 1 km = 1000 m
,तब 360 km= 360×1000 m
तथा समय 1 घण्टा (h) = 60×60 सेकंड (s)
चाल के सूत्र से = 360×100060×60
चाल = 10 m/s
इस प्रकार km/h को m/s में बदला जाता है।
कुछ वस्तुओं की चाल बहुत ही तेज होती है। जैसे अंतरिक्ष में जाने वाले रॉकेटों की चाल 8 km/s तक होती है तथा कुछ की चाल बहुत ही धीमी होती है। जैसे - कछुआ लगभग 10 cm/s की चाल से चल सकता है। यदि किसी वस्तु की चाल दी गई हो, तब दिए गए समय में उस वस्तु द्वारा तय की गई दूरी को ज्ञात किया जा सकता है। इसके लिए केवल चाल को समय से गुणा करना पड़ता है -
तय की गई दूरी = चाल×समय
इसी सूत्र के द्वारा यदि किसी वस्तु की चाल एवं दूरी ज्ञात हो, तो लिया गया समय ज्ञात किया जा सकता है -

वाहनों में चाल एवं दूरी का मापन
हमने सभी प्रकार के वाहन जैसे - मोटर साइकिल, कार, बस आदि सभी देखे ही हैं तथा इनमें बैठकर सफर भी किया है। बच्चों क्या आपने कभी यह ध्यान दिया है कि सभी वाहनों में दूरी एवं चाल के मापन के लिए मीटर लगा होता है, जिसकी सहायता से हम वाहन की चाल एवं वाहन द्वारा तय की गई दूरी ज्ञात कर सकते हैं। आइए इन मीटरों के बारे में जानें -
चालमापी या स्पीडोमीटर : बच्चों जब कभी आप किसी भी प्रकार के वाहन देखें, तो उस वाहन के डैशबोर्ड में आपको एक मीटर दिखाई देगा। जैसा कि नीचे चित्र में दिखाया गया है। इस मीटर के द्वारा वाहन की चाल सीधे ही km/h में ज्ञात किया जा सकता है।

पथमापी या ओडोमीटर : यह मीटर भी वाहन के डैशबोर्ड में स्थित होता है। इसमें नंबर लिखे होते हैं। जैसा कि नीचे चित्र में देखा जा सकता है। पथमापी या ओडोमीटर के द्वारा उस वाहन के द्वारा तय की गई दूरी को ज्ञात किया जा सकता है।

ग्राफ
ग्राफ एक ऐसी विधि है, जिसकी सहायता से हम दो चर राशियों के मध्य सम्बन्ध स्थापित कर सकते हैं। चर राशि का आशय होता है, ऐसी राशि जिनके मान परिवर्तित हो सकते हैं। इन दो चर राशियों में से एक राशि स्वतंत्र रूप से बदलती रहती हैं, इसे स्वतंत्र चर राशि कहते हैं तथा दूसरी चर राशि पहली स्वतंत्र चर राशि के बदलने से बदलती है। इसे आश्रित चर राशि कहते हैं। स्वतंत्र चर राशि को X-अक्ष में तथा आश्रित चर राशि को Y-अक्ष में रखते हैं। ग्राफ बनाने के लिए ग्राफ पेपर का उपयोग किया जाता है। जिसे नीचे चित्र में देखा जा सकता है।
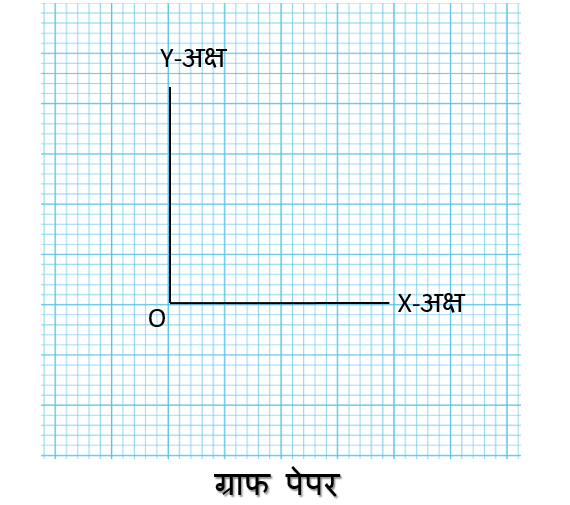
ग्राफ के प्रकार : ग्राफ के मुख्यतः 3 प्रकार होते हैं, जो निम्न हैं -
- स्तम्भ ग्राफ
- वृत्तारेख या पाई ग्राफ
- रेखा ग्राफ
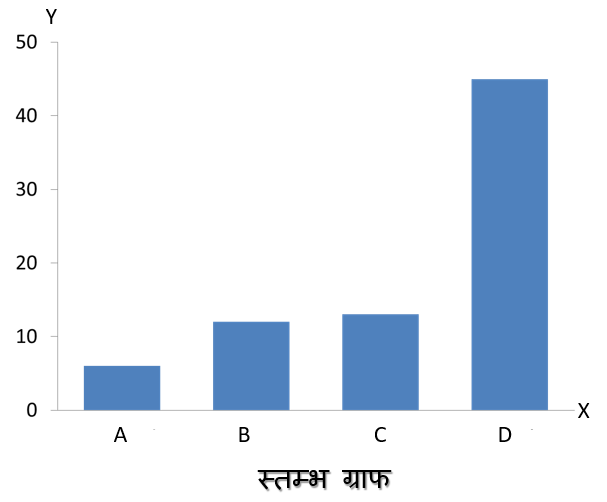
वृत्तारेख या पाई ग्राफ : जैसा के इसके नाम से स्पष्ट होता है कि वृत्तारेख या पाई ग्राफ की आकृति वृत्ताकार होती है। पाई ग्राफ में 360 अंश का कोण होता है, जिसे विभिन्न भागों में विभाजित करके आंकड़ों को प्रदर्शित किया जाता है। नीचे एक वृत्तारेख या पाई ग्राफ का चित्र प्रदर्शित किया गया है, जिसमें वायुमंडलीय गैसों का प्रतिशत दर्शाया गया है।
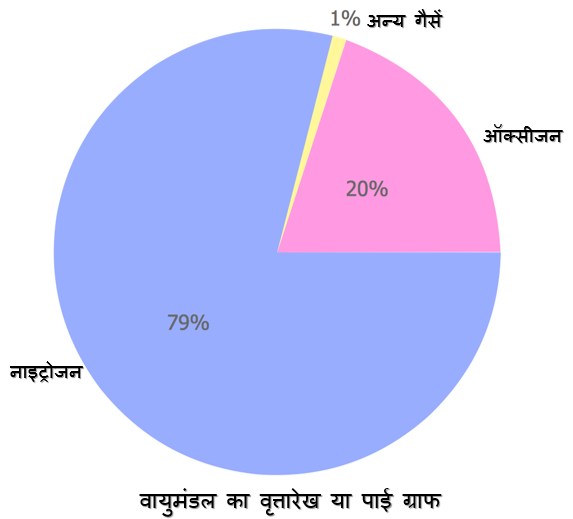
रेखा ग्राफ : इस प्रकार के ग्राफ में आंकड़ों को X-अक्ष तथा Y-अक्ष के आधार पर दोनों अक्षों में बिंदुओं के क्रम में अंकित किया जाता है, फिर इन बिंदुओं को परिस्थिति के आधार पर मिलाते है, जिससे हमें एक रेखा प्राप्त होती है। इसी कारण से इसे रेखा ग्राफ कहते हैं।

रेखा ग्राफ सबसे अधिक उपयोग में आने वाला ग्राफ है। यह बहुत ही सरल होता है, इस ग्राफ का उपयोग सभी जगह किया जा सकता है। दूरी-समय ग्राफ में रेखा ग्राफ का उपयोग किया जाता है।
ग्राफ बनाने की विधि : ग्राफ खींचने के लिए हमें ग्राफ पेपर की आवश्यकता होती है। नीचे एक चित्र दिया गया है, पढ़ने के साथ में उसे भी देखें। इस ग्राफ पेपर में एक दूसरे से लम्बवत दो रेखाएँ खींचते हैं। जिसकी क्षैतिज रेखा को X', O तथा X नाम देते हैं, इसे X-अक्ष कहते हैं एवं ऊर्ध्वाधर रेखा को Y', O तथा Y नाम देते हैं, इसे Y-अक्ष कहते हैं। इन दोनों रेखाओं के मध्य बिन्दु को O बिन्दु या प्रतिच्छेद बिन्दु कहते हैं। यहाँ X-अक्ष पर धनात्मक मानों को OX में प्रदर्शित किया जाता है तथा Y-अक्ष के धनात्मक मानों को OY में प्रदर्शित किया जाता है। X' तथा Y' ऋणात्मक होते है।
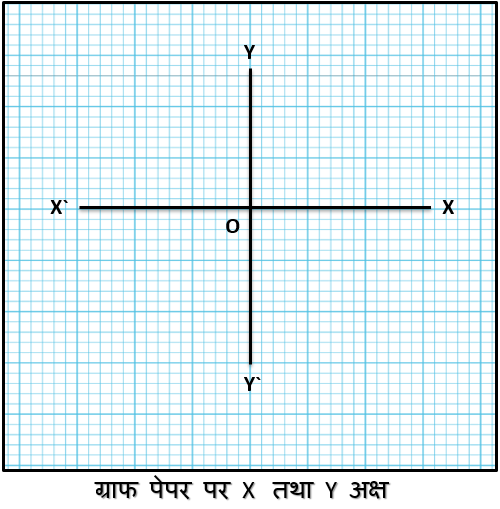
दूरी-समय ग्राफ
ऐसा ग्राफ जिसमें दूरी तथा समय के आंकड़ों को प्रदर्शित किया जाता है, उसे दूरी-समय ग्राफ कहते हैं। इसके लिए हमें दूरी तथा समय के आकड़ों की आवश्यकता होती है। इसे एक उदाहरण के द्वारा समझने का प्रयास करते हैं -
उदाहरण - दूरी-समय ग्राफ बनाने के लिए हम किसी कार द्वारा चली गई दूरी तथा समय का आवलोकन करके नीचे एक सारणी में उन्हें भरते हैं, फिर उन आकड़ों से दूरी-समय ग्राफ बनाएंगे।
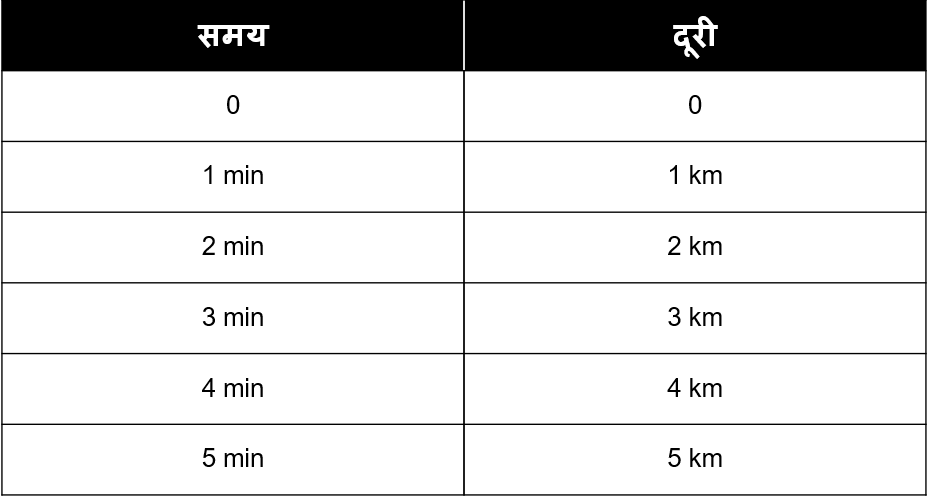
दूरी-समय ग्राफ बनाने के निम्न चरण :
- दूरी समय ग्राफ बनाने के लिए एक ग्राफ पेपर में दो लम्बवत रेखाएं खींचते हैं, जिन्हें OX तथा OY नाम देते हैं।
- दोनों अक्षों में से X-अक्ष पर समय को दर्शाते हैं, क्यूंकी समय एक स्वतंत्र चर राशि है तथा Y-अक्ष में दूरी को दर्शाते हैं, क्यूंकी दूरी आश्रित चर राशि है।
- दोनों राशियों को निरूपित करने के लिए पैमाने का चुनाव करते हैं। जैसे दूरी को निरूपित करने के लिए एक पैमाना चुनते हैं तथा समय को निरूपित करने के लिए एक पैमाना चुनते हैं। उदाहरण कार की गति के लिए पैमाने -
समय 1 min = 1 cm
दूरी 1 km = 1 cm - यह पैमाना इसलिए चुना जाता है कि आकड़ों को अक्षों पर एक निश्चित क्रम में रखा जा सके।
- अब इन चुने गए पैमानों के अनुसार दूरी तथा समय के आकड़ों या मानों को अपने-अपने अक्षों पर रखते हैं। जैसे Y-अक्ष पर दूरी को 1 km, 2 km, 3 km… तथा इसी प्रकार X-अक्ष पर समय को 1 min, 2 min, 3 min… आदि को अंकित करते हैं । इसे चित्र में देखा जा सकता है।
- अब सारणी के अनुसार दूरी तथा समय के सभी मानो को ग्राफ पेपर में निरूपित करने के लिए प्रत्येक मानो के मध्य बिन्दु अंकित करने होंगे। जिससे हमें दूरी समय के लिए रेखा ग्राफ प्राप्त हो सके।
- ऊपर चित्र में देखा जा सकता है कि किस प्रकार दूरी तथा समय के मानो को अंकित किया गया है, बिन्दु O को शून्य माना जाता है, अतः इसे प्रारम्भिक बिन्दु भी कहा जा सकता है। दूरी तथा समय के प्रत्येक मान जैसे 1 min समय से लम्बवत रेखा खींचते हैं एवं 1 km दूरी से लम्बवत रेखा खींचते है तथा जहाँ पर दोनों रेखाएँ एक दूसरे को काटती है, वहाँ एक बिन्दु बना लेते हैं। ऐसा सभी मानों के लिए करते हैं, इससे हमें एक सरल रेखा प्राप्त होती है, अतः यही सरल रेखा कार की गति के लिए दूरी-समय ग्राफ को दर्शाती है।
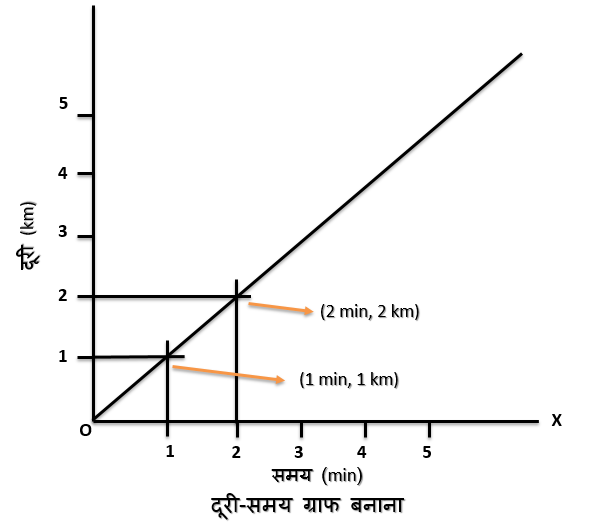
ग्राफ पेपर में ग्राफ खींचने के लिए पैमाने का चुनाव करते समय कुछ मुख्य बातों को ध्यान में रखना आवश्यक है, जैसे -
- प्रत्येक राशि के अधिकतम एवं न्यूनतम मानों के बीच अंतर ज्ञात होना चाहिए।
- प्रत्येक राशि के मध्यवर्ती (बीच में स्थित) मान ज्ञात होना चाहिए, जिससे उन्हें ग्राफ पर चुने गए पैमाने के आधार पर अंकित करना सरल हो।
- जिस पेपर पर ग्राफ खींचना है, उसके अधिकतम भाग का उपयोग करना चाहिए।
उदाहरण - बच्चों मान लीजिए जब कभी हम किसी वाहन में कहीं दूर किसी पर्यटन स्थल जायें, तो जब वाहन चलना प्रारंभ करता है, तब उसके ओडोमीटर का प्रारम्भिक पाठ्यांक नोट कर लेते हैं। इसके पश्चात हर 30 मिनट में ओडोमीटर का पाठ्यांक नोट करते हैं, जब तक के हम अपने पर्यटन स्थल तक नहीं पहुँच जाते। ओडोमीटर के पाठ्यांक के साथ समय भी नोट करते जाते हैं। इससे हम जान सकते हैं कि हमने कितने समय में कितनी दूरी तय की तथा हमारे घर से वह पर्यटन स्थल कितनी दूर है ? इसे समझने के लिए नीचे एक सारणी दी गई है।
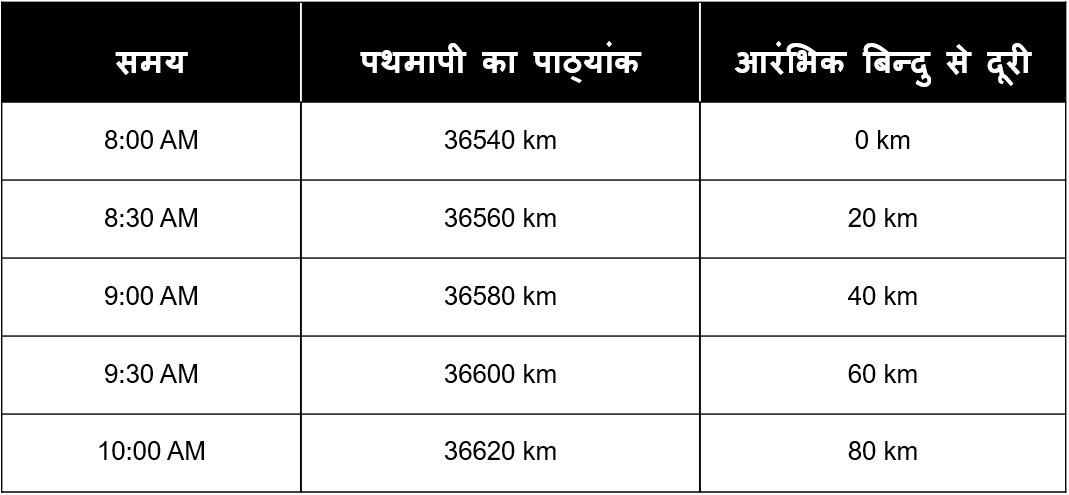
ऊपर दिए गए सारणी में बस द्वारा चली गई दूरी तथा दूरी तय करने में लिए गए समय को नोट किया गया है। बस द्वारा कुल 80 km दूरी तय कि गई है, अब इसे ग्राफ पेपर में दर्शाने के लिए पैमाने के रूप में यदि हम 1 km = 1 cm लेंगे, तो इसे ग्राफ पेपर में निरूपित करना संभव नहीं होगा। इस कारण सही पैमाने का चुनाव करना बहुत ही आवश्यक है। यदि हम 10 km = 1 cm लेंगे, तो हमें ग्राफ पेपर पर 8 cm की रेखा खींचने की आवश्यकता होगी, जो कि बिल्कुल ही सही पैमाना है।
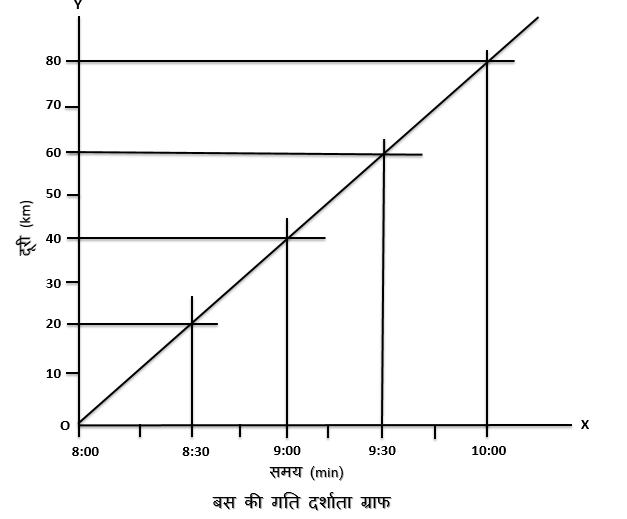
ऊपर दिए चित्र में बस की गति का दूरी-समय ग्राफ प्रदर्शित किया गया है। अब हम इसकी सहायता से किसी भी समय के लिए बस द्वारा चली गई दूरी का पता लगा सकते हैं। जैसे यदि हमें जानना हो कि 8:45 AM में बस ने कितनी दूरी तय की ? तो हम इसे प्रदर्शित ग्राफ द्वारा ज्ञात कर सकते हैं।
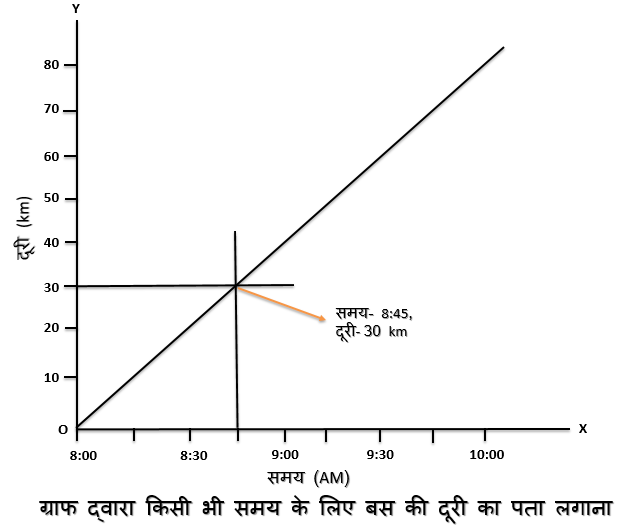
इसे ज्ञात करने के लिए हम 8:30 AM तथा 9:00 AM के बीच के समय को देखेंगे, जो ग्राफ के X-अक्ष में स्थित है। वहाँ एक बिन्दु लगाएंगे तथा उससे लम्बवत ऊपर की ओर रेखा खिचेंगे। फिर हम उस जगह एक बिन्दु अंकित करेंगे, जहाँ ये रेखा ग्राफ को काटती है तथा अंकित बिन्दु से एक लम्बवत रेखा Y-अक्ष की ओर खिचेंगे तथा देखते हैं कि रेखा Y-अक्ष के किस पैमाने को छूती है ? अतः हम पाते हैं कि बस ने 8:45 AM तक 30 km तक की दूरी तय की। इस प्रकार हम दूरी-समय ग्राफ द्वारा किसी भी गतिशील वस्तु की चाल, दूरी तथा दूरी तय करने में लगा समय ज्ञात कर सकते हैं।
सारांश
- जब कोई वस्तु समय के साथ अपनी अवस्था में परिवर्तन करता है, तो इस घटना को गति कहते हैं। सरल रेखीय गति, वर्तुल गति, घूर्णन गति, दोलन गति, आवर्ती गति, अनावर्ती गति ये सभी गति के प्रकार हैं।
- किन्ही दो घटनाओं के बीच के काल-अंतर (अंतराल) को समय कहा जाता है, इसका मूल मात्रक सेकंड (s) होता है।
- सरल लोलक (पेंडुलम) में आवर्ती गति एवं दोलन गति दोनों होती है। सरल लोलक (पेंडुलम) का उपयोग घड़ी बनाने में भी किया जाता है।
- दिए गए निश्चित समय में किसी वस्तु द्वारा तय की गई दूरी को उस वस्तु की चाल कहते हैं।
- किसी गतिशील वस्तु की चाल से हम यह ज्ञात कर सकते हैं कि वह वस्तु अन्य गतिशील वस्तुओं से तेज है या धीमी।
- वाहनों में चाल मापने के लिए चालमापी या स्पीडोमीटर लगा होता है तथा दूरी मापने के लिए पथमापी या ओडोमीटर लगा होता है।
- ऐसी विधि जिसके द्वारा हम दो चर राशियों के मध्य संबंध प्रदर्शित कर सकते हैं, उसे ग्राफ कहते हैं। दूरी तथा समय के मध्य जो ग्राफ बनाया जाता है, उसे दूरी-समय ग्राफ कहते हैं।
- दूरी-समय ग्राफ के द्वारा हम किसी भी गतिशील वस्तु द्वारा तय की गई दूरी तथा दूरी तय करने में लगा समय ज्ञात कर सकते हैं।