SYMMETRY for Class 7 MATHS
INTRODUCTION
Baccho aapne apni previous classes m symmetry k baare m dha hua hai aur isse related topics bhi jaane hai jaise ki line of symmetry and reflection. Symmetry ek aisa concept hai jise hum apni day to day life k saath bohot zyada relate kr skte hai. We see symmetry around us in various places. Symmetry is also a very common term. Iss chapter m hum symmetry se related apn previous understanding p build krte hue aage pdhenge. We'll learn about line of symmetry in polygons, rotational symmetry, etc. So let's get started!
SYMMETRY
A shape is said to be symmetric if it can be divided into two more identical pieces which are placed in an organized way. For example, when you are told to cut out a ‘heart’ from a piece of paper, you simply fold the paper, draw one-half of the heart at the fold and cut it out to find that the other half exactly matches the first half. The heart carved out is an example of symmetry. Similarly, a regular pentagon when divided as shown in the image below, has one part symmetrical to the other.
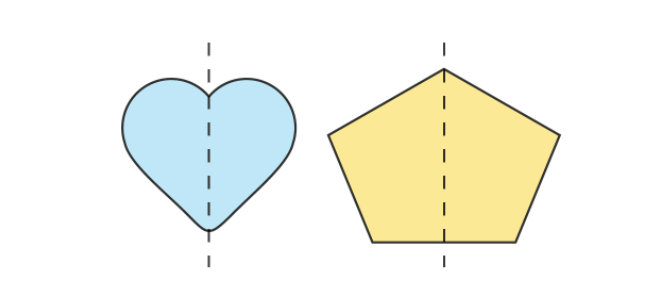
The definition of Symmetry in Math, states that “symmetry is a mirror image”, i.e., when an image looks identical to the original image after the shape is being turned or flipped, then it is called symmetry. Symmetricity exists in patterns. It is a balanced and proportionate similarity found in two halves of an object, which means one-half is the mirror image of the other half. Symmetric objects are found all around us in day-to-day life, in art, and in architecture.

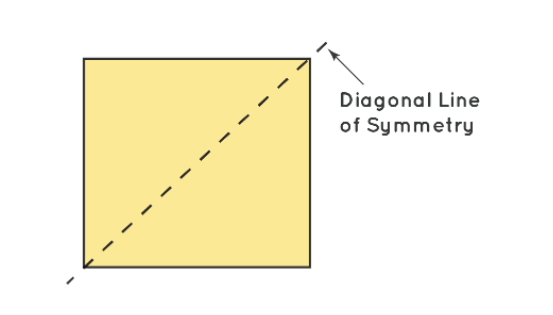
LINE OF SYMMETRY
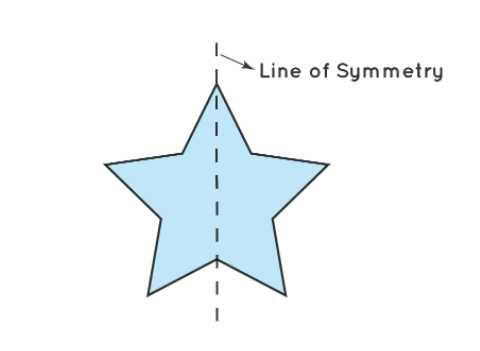
The line of symmetry is a line that divides an object into two identical pieces. Here, we have a star and we can fold it into two equal halves. When a figure is folded in half, along its line of symmetry, both the halves match each other exactly. This line of symmetry is called the axis of symmetry.
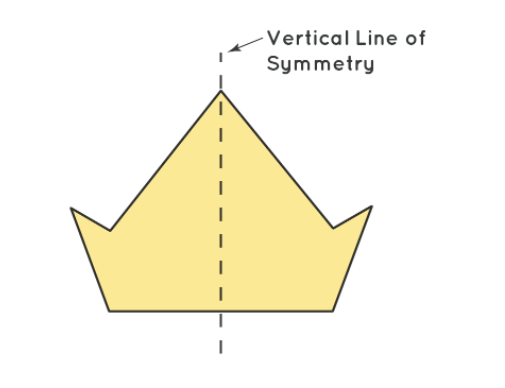
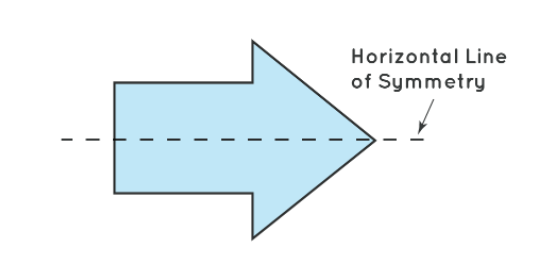
The line of symmetry can be categorized based on its orientation as:
Example 1
Give three examples of shapes with no line of symmetry.
Any closed figure which does not have any line segment in it can be example of this questions. some are given in video as example
LINES OF SYMMETRY FOR REGULAR POLYGONS
Baccho, aapne apne previous chapters m pdha hai ki polygons vo closed figures hote hai jo ki line segments ko join krke bnte hai. To form a polygon you need atleast 3 line segments and this polygon Is called a triangle. Regular polygons vo polygons hote hai jinki line segments equal lengths ki hoti hai. Which implies that a regular polygon of four sides is a square, a regular polygon of five sides is called a regular petagon and so on. Regular polygons ka relation symmetry se iss tarah se hota hai ki har regular polygon ki utni lines of symmetry hoti hai jitni unki sides hoti hai. Therefore, a square has 4 lines of symmetry, a regular pentagon has 5 lines of symmetry and so on. Baccho, iska mtlb hai ki jab hum inn lines of symmetry k along kisi regular polygon ko fold krenge to hume identical fugure milengi. Look at the following figures for better understanding:

Example 2
What other name can you give to the line of symmetry of:
(a) an isosceles triangle?
(b) a circle?
(a) In an isosceles triangle two sides are equal. So, the line of symmetry in an isosceles triangle is the median of the triangle that is bisects the third side.
(b) In a circle, line of symmetry is diameter that connects circle with its center.
ROTATIONAL SYMMETRY
When an object is rotated in a particular direction, around a point, then it is known as rotational symmetry, also known as radial symmetry. Rotational symmetry exists when a shape is turned, and the shape is identical to the origin. The angle of rotational symmetry is the smallest angle at which the figure can be rotated to coincide with itself and the order of symmetry is how the object coincides with itself when it is in rotation.
In geometry, there are many shapes that depict rotational symmetry. For example, figures such as circle, square, rectangle depict rotational symmetry. The following image shows how the structure of a starfish follows rotational symmetry. If you turn or rotate the starfish about point P, it will still look the same from all directions. The famous Ferris wheel, the London Eye, is an example of rotational symmetry. You can find many objects in real life that have rotational symmetry like wheels, windmills, road-signs, ceiling fans, and so on.


LINE SYMMETRY AND ROTATIONAL SYMMETRY
Baccho, aapne abhi line symmetry k baare m aur rotational symmetry k baare m pdha. Aapne dekha ki kuch shapes hoti hai jinme sirf line symmetry exist krti hai aur kuch shapes hoti hai jinme sirf rotational symmetry exist krti hai yaani ki unhe turn krne p bhi figure same rehti hai. In this section we'll see if there are any shapes or figures which can have both line and rotational symmetry. Can you think of a shape like that?
The most perfect example is a circle. Hum ek circle ko unlimited number of lines of symmetry se divide kr skte hai aur hum ek circle ko jitni baari bhi jis bhi angle se turn kre uski shape same hi rehti hai. Observe any circle pattern. Every line through the centre (that is every diameter) forms a line of (reflectional) symmetry and it has rotational symmetry around the centre for every angle. This is an example of a line and rotational symmetry
Example 3
If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Yes, if a figure has two or more lines of symmetry, it should have rotational symmetry of order more than 1
Example 4
Draw, wherever possible, a rough sketch of:
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
1) order of rectangle= 3600900=4
order of triangle=36001200=3
2) a triangle can be drawn with only line symmetry and no rotational symmetry of order more than 1.
3) a parallelogram is a quadrilateral with a rotational symmetry of order more than 1 but not a symmetry.
4) A trapezium is a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
SUMMARY
1. A figure has line symmetry, if there is a line about which the figure may be folded so that the two parts of the figure will coincide.
2. Regular polygons have equal sides and equal angles. They have multiple (i.e., more
than one) lines of symmetry.
3. Each regular polygon has as many lines of symmetry as it has sides.
IMAGE 10
4. Mirror reflection leads to symmetry, under which the left-right orientation have to be taken care of.
5. Rotation turns an object about a fixed point.
This fixed point is the centre of rotation. The angle by which the object rotates is the angle of rotation. A half-turn means rotation by 180∘; a quarter-turn means rotation by 90∘. Rotation may be clockwise or anticlockwise.
6. If, after a rotation, an object looks exactly the same, we say that it has a rotational
symmetry.
7. In a complete turn (of 360∘), the number of times an object looks exactly the same is called the order of rotational symmetry. The order of symmetry of a square, for example, is 4 while, for an equilateral triangle, it is 3.
8. Some shapes have only one line of symmetry, like the letter E; some have only rotational symmetry, like the letter S; and some have both symmetries like the letter H.
The study of symmetry is important because of its frequent use in day-to-day life and
more because of the beautiful designs it can provide us.
Let's Revise
1. Baccho iss chapter m humne symmetry se related topics k baare m pdha. Ye ek aisa geometrical concept hai jiske according jab ek figure do ya do se zyada identical parts m divide ho skti hai (passing through its centre) then it is called symmetric.
2. Humne line of symmetry k baare m pdha aur jaana ki line of symmetry basically vo axis hota hai jiske through ek figure ko fold ya cut krne par hume identical parts milte hai.
3. We related line of symmetry with regular polygons and learnt that in regular polygons, lines of symmetry are equal to the number of sides of the polygons.
4 Baccho uske baad humne rotational symmetry k baare m pdha. Rotational symmetry tab hoti hai jab ek figure o ek particular angle p rotate krne k baad bhi vo same figure m rehti hai.
5. Lastly, humne line of symmetry and rotational symmetry with rotational symmetry k baare m pdha. Yaani ki aisi figures jinme line symmetry bhi exit krti hai aur unhe turn/rotate krne par bhi figure same rehti hai.